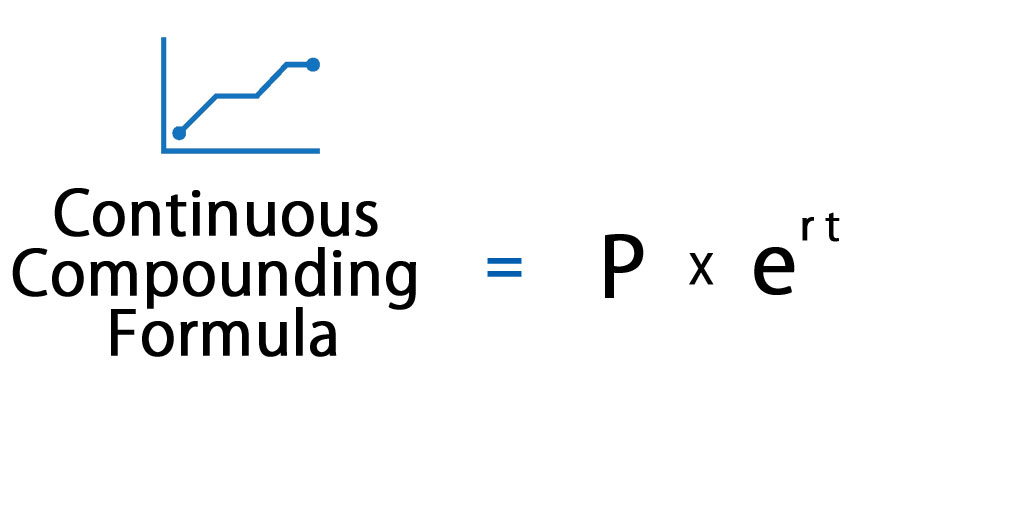कंटिन्युवस कंपाउंडिंग फ़ॉर्मूला (सामग्री की तालिका)
- कंटिन्युवस कंपाउंडिंग फ़ॉर्मूला
- कंटिन्युवस कंपाउंडिंग कैलकुलेटर
- एक्सेल में कंटिन्युवस कंपाउंडिंग फॉर्मूला (एक्सेल टेम्पलेट के साथ)
कंटिन्युवस कंपाउंडिंग फ़ॉर्मूला
कंटिन्युवस कंपाउंडिंग अवधारणा पर कूदने से पहले, आइए समझते हैं कि पहले ब्याज की कंटिन्युवस कंपाउंडिंग क्या है। चक्रवृद्धि ब्याज का अर्थ है कि प्रत्येक वर्ष कमाने वाले ब्याज को उसके मूलधन में जोड़ा जाता है, जिससे कि राशि केवल बढ़ती नहीं है, यह साधारण ब्याज दर की तुलना में बढ़ती दर से बढ़ती है – वित्त में सबसे उपयोगी अवधारणाओं में से एक है। यह शेयर बाजार में लंबी अवधि के निवेश की योजना से लेकर व्यक्तिगत बचत योजना तक सबका आधार है। यह राशि पर मुद्रास्फीति के प्रभावों का भी ध्यान रखता है, और देनदार के अनुपात का भुगतान करने का महत्व कैलक्यूलेटर (एक्सेल टेम्पलेट)।
लगातार चक्रवृद्धि ब्याज दर हर पल जुड़ती जाती है। इससे गणना कठिन हो जाती है। यह किसी भी वित्तीय संस्थान द्वारा ब्याज दर के आरोपों के लिए उपयोग नहीं किया जाता है क्योंकि कंटिन्युवस कंपाउंडिंग राशि और दैनिक चक्रवृद्धि राशि में बहुत कम अंतर होता है। बैंक अपने कुछ उत्पादों में दैनिक चक्रवृद्धि ब्याज राशि का उपयोग करते हैं।
कंटिन्युवस कंपाउंडिंग का सूत्र निम्नानुसार है:
कंटिन्युवस कंपाउंडिंग फॉर्मूला अर्जित ब्याज की गणना करता है जो कि अनंत समय अवधि के लिए निरंतर कंपाउंड होता है।
कहा पे,
पी = प्रधान राशि (राशि का वर्तमान मूल्य)
t = समय (समय वर्ष है)
r = ब्याज की दर।
उपरोक्त गणना अनंत समयावधि में ब्याज की कंटिन्युवस कंपाउंडिंग मानती है। जैसा कि उल्लेख किया गया समय अवधि अनंत है, घातांक फ़ंक्शन (ई) वर्तमान निवेश राशि के गुणा में मदद करता है। यह वर्तमान ब्याज दर और समय अवधि से गुणा किया जाता है। बड़ी संख्या में निवेश राशि के बावजूद, एक्सेल में कंटिन्युवस कंपाउंडिंग के माध्यम से अर्जित कुल ब्याज के बीच का अंतर पारंपरिक चक्रवृद्धि ब्याज की तुलना में समान है।
उदाहरण और कंटिन्युवस कंपाउंडिंग फॉर्मूला की व्याख्या
8% की ब्याज दर और 1 वर्ष की समयावधि के साथ मूल $ 10,000 पर चक्रवृद्धि ब्याज की गणना करें । यौगिक आवृत्ति एक वर्ष, अर्ध–वार्षिक, त्रैमासिक, मासिक और कंटिन्युवस कंपाउंडिंग है।
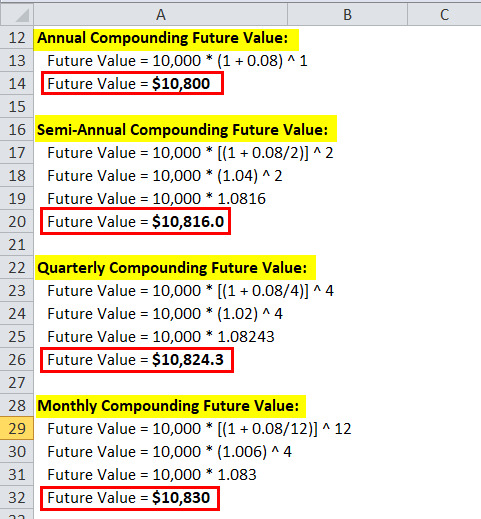
वार्षिक मिश्रित भविष्य का मूल्य:
- भविष्य का मूल्य = 10,000 * (1 + 0.08) ^ 1
- भविष्य का मूल्य = $ 10,800
अर्ध–वार्षिक मिश्रित भविष्य मूल्य:
- भविष्य का मूल्य = 10,000 * [(1 + 0.08 / 2)] ^ 2
- भविष्य का मूल्य = 10,000 * (1.04) ^ 2
- भविष्य का मूल्य = 10,000 * 1.0816
- भविष्य का मूल्य = $ 10,816.0
भविष्य के मूल्य की त्रैमासिक गणना:
- भविष्य का मूल्य = 10,000 * [(1 + 0.08 / 4)] ^ 4
- भविष्य का मूल्य = 10,000 * (1.02) ^ 4
- भविष्य का मूल्य = 10,000 * 1.08243
- भविष्य का मूल्य = $ 10,824.3
मासिक मूल्य भविष्य के मूल्य:
- भविष्य का मूल्य = 10,000 * [(1 + 0.08 / 12)] ^ 12
- भविष्य का मूल्य = 10,000 * (1.006) ^ 4
- भविष्य का मूल्य = 10,000 * 1.083
- भविष्य का मूल्य = $ 10,830
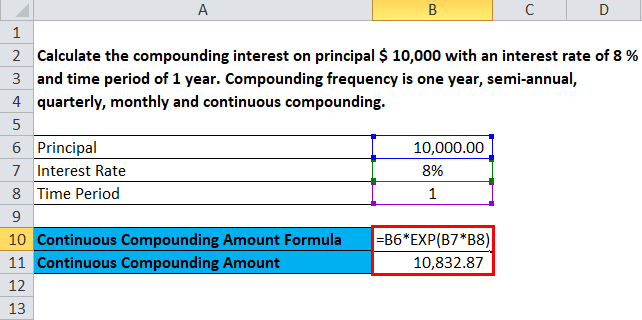
कंटिन्युवस कंपाउंडिंग भविष्य मूल्य:
- भविष्य का मूल्य = 10,000 * ई08
- भविष्य का मूल्य = 10,000 * 1.08328
- भविष्य का मूल्य = $ 10,832.87
जैसा कि विभिन्न आवृत्तियों के साथ चक्रवृद्धि की गणना के उपरोक्त उदाहरण से देखा जा सकता है, निरंतर चक्रवृद्धि से गणना की गई ब्याज $ 832.9 है जो मासिक चक्रवृद्धि से केवल 2.9 डॉलर अधिक है। तो यह निरंतर चक्रवृद्धि ब्याज दर की तुलना में व्यावहारिक जीवन में मासिक या दैनिक चक्रवृद्धि ब्याज दर का उपयोग करने का मामला बनाता है।
महत्व और उपयोग
कंटिन्युवस कंपाउंडिंग फ़ॉर्मूला का महत्व है:
- वार्षिक आधार, त्रैमासिक आधार या मासिक आधार पर ब्याज की कंटिन्युवस कंपाउंडिंग के बजाय, सतत चक्रवृद्धि एक्सेल कुशलतापूर्वक नियमित रूप से लाभ को फिर से जुटाएगी।
- निरंतर चक्रवृद्धि प्रभाव, ब्याज की कंटिन्युवस कंपाउंडिंग को उसी ब्याज दर पर पुनर्निर्मित करने की अनुमति देता है जिससे निवेशक को एक घातीय दर पर रिटर्न अर्जित करने का अवसर मिलता है।
- निरंतर चक्रवृद्धि यह निर्धारित करती है कि यह न केवल मूल राशि है जो धन अर्जित करेगी बल्कि ब्याज की कंटिन्युवस कंपाउंडिंग भी राशि को गुणा करती रहेगी।
यौगिक वार्षिक आधार, अर्ध-वार्षिक आधार, त्रैमासिक आधार, दैनिक आधार या निरंतर आधार पर किया जा सकता है। इन समय अवधियों के बीच अंतर, समय अवधि को समाप्त करने के बाद जो भी ब्याज अर्जित किया जाता है उसे नए प्रमुख के रूप में माना जाता है। उदाहरण के लिए, यदि कंपाउंडिंग आवृत्ति अर्ध-वार्षिक है, तो छह महीने के बाद मूलधन में ब्याज जोड़ा जाएगा, यह चक्र परिपक्वता तक जारी रहता है। एक और समय सीमा के साथ मामला है, वार्षिक ब्याज एक साल के बाद जोड़ा जाता है, के लिए तिमाही ब्याज तीन महीने के बाद जोड़ा जाता है, के लिए दैनिक ब्याज अगले दिन जोड़ा जाता है।
कैलकुलेटर
आप निम्न कंटिन्युवस कंपाउंडिंग कैलकुलेटर का उपयोग कर सकते हैं
| First Value | |
| Second Value | |
| Formula = | |
| First Value x e(Second Value x Formula =) | |
| = | 0 x e(0 x 0) = 0 |
एक्सेल में कंटिन्युवस कंपाउंडिंग फॉर्मूला (एक्सेल टेम्पलेट के साथ)
यहां हम एक्सेल में कंटिन्युवस कंपाउंडिंग फ़ॉर्मूला का एक ही उदाहरण देंगे। यह बहुत आसान और सरल है। आपको तीन इनपुट यानी मूल राशि, ब्याज दर और समय प्रदान करना होगा।
आप दिए गए टेम्पलेट में फॉर्मूला का उपयोग करके आसानी से कंटीन्यूअस कंपाउंडिंग की गणना कर सकते हैं।
सबसे पहले, हमें फॉर्मूला का उपयोग करके कंटिन्युवस कंपाउंडिंग राशि की गणना करने की आवश्यकता है
फिर, हमें नियमित कंपाउंडिंग पर उसी के प्रभाव की गणना करने की आवश्यकता है:
अनुशंसित लेख
यह कंटिन्युवस कंपाउंडिंग फ़ॉर्मूला का एक मार्गदर्शक रहा है। यहां हम व्यावहारिक उदाहरणों के साथ इसके उपयोगों पर चर्चा करते हैं। हम आपको डाउनलोड करने योग्य एक्सेल टेम्पलेट के साथ कंटिन्युवस कंपाउंडिंग कैलकुलेटर भी प्रदान करते हैं। अधिक जानने के लिए आप निम्नलिखित लेख भी देख सकते हैं –
- टैक्स क्रेडिट बनाम टैक्स कटौती – तुलना
- सरल ब्याज दर बनाम चक्रवृद्धि ब्याज दर के बीच अंतर
- छूट दर बनाम ब्याज दर – शीर्ष अंतर
- सर्वश्रेष्ठ बिक्री के लिए शीर्ष तकनीक ऑनलाइन