Updated July 28, 2023

Correlation Formula (Table of Contents)
- Correlation Formula
- Examples of Correlation Formula (With Excel Template)
- Correlation Formula Calculator
Correlation Formula
Correlation is widely used in portfolio measurement and the measurement of risk. Correlation measures the relationship between two independent variables and can be defined as the degree of relationship between two stocks in the portfolio through correlation analysis.
The correlation measure is known as the coefficient of correlation and is a primary measure of the risk. The correlation analysis gives us an idea about the degree & direction of the relationship between the two variables under study.
The formula for correlation is equal to Covariance of return of asset 1 and Covariance of asset 2 / Standard.
Deviation of asset 1 and a Standard Deviation of asset 2.
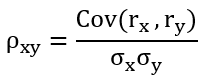
- ρxy = Correlation between two variables
- Cov(rx, ry) = Covariance of return X and Covariance of return of Y
- σx = Standard deviation of X
- σy = Standard deviation of Y
Correlation is based on the cause of effect relationship, and there are three kinds of correlation in the study, which is widely used and practiced.
- Positive Correlation – A positive correlation exists between two variables when they are said to move in the same direction. For example height and weight.
- Negative Correlation – There is said to exist a negative correlation between two variables when the variable change in the opposite direction. For example, the law of demand, quantity, and supply.
- No Correlation – There exists no correlation between two variables when there is no movement of a direct relationship between the two variables. That is, they do not have any relationship in the movement of each other.
Examples of Correlation Formula (With Excel Template)
Let’s take an example to understand the formula calculation better.
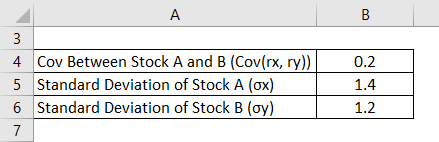
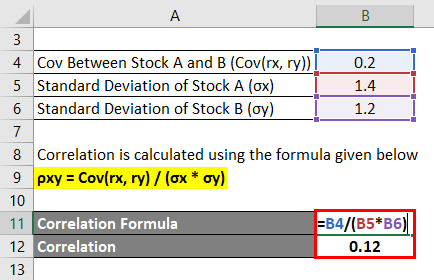
Correlation Formula – Example #1
A fund manager wants to calculate the coefficient of correlation between two stocks in the debt real estate assets portfolio.
Solution:
Correlation is calculated using the formula given below
ρxy = Cov(rx, ry) / (σx * σy)
- Correlation = 0.2 / (1.4 * 1.2)
- Correlation = 0.12
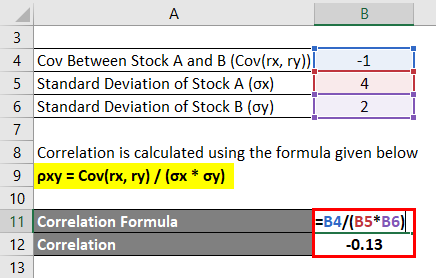
Correlation Formula – Example #2
A student wants to calculate the coefficient of correlation between two stocks in the portfolio.
Solution:
Correlation is calculated using the formula given below
ρxy = Cov(rx, ry) / (σx * σy)
- Correlation = -1 / (4 * 2)
- Correlation = -0.13
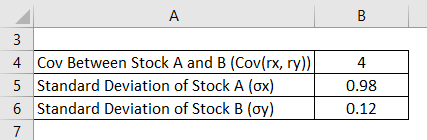
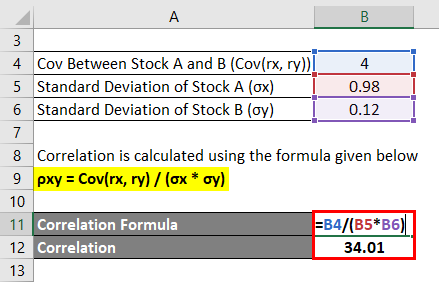
Correlation Formula – Example #3
A VC fund is evaluating its portfolio, and it wants to calculate the coefficient of correlation between two stocks in the portfolio.
Solution:
Correlation is calculated using the formula given below
ρxy = Cov(rx, ry) / (σx * σy)
- Correlation = 4 / (0.98 * 0.12)
- Correlation = 34.01
Explanation
Correlation is used in the measure of the standard deviation.
- A coefficient of 1 means a perfect positive relationship – as one variable increases, the other increases proportionally.
- A coefficient of -1 means a perfect negative relationship – as one variable increases, the other decreases proportionally.
- A coefficient of 0 means no relationship between two variables – the data points are scattered throughout the graph.
Relevance and Uses of Correlation
- Correlation empowers the researcher to detect the unethically occurring variables to test experimentally.
- Correlation is very important in Psychology and Education as a measure of the relationship between test scores and other performance measures.
- It is an important formula that tells the user the strength and the direction of a linear relationship between variable x and y. The greater the absolute value, the stronger the relationship tends to be.
- Researchers should avoid inferring causation from correlation, which is unsuited for analysis of the agreement. Correlational research has had and will continue to have an important role in quantitative research in exploring the nature of the relations among a collection of variables.
Correlation Formula Calculator
You can use the following Correlation Calculator
| Con(rx,ry) | |
| σx | |
| σy | |
| ρxy | |
| ρxy = |
|
||||||||
|
Recommended Articles
This is a guide to Correlation Formula. Here we have discussed how to calculate Correlation along with practical examples. We also provide a Correlation calculator with a downloadable excel template. You may also look at the following articles to learn more –