Updated March 17, 2023

Introduction to Math Functions in Python
In Python, Math functions are a collection of pre-defined mathematical actions with generic implicit values that can be directly fetched for the mathematical operations in the program. There are several such math functions in python, like constants (pi for return value 3.141592, E for return value 0.718282 , nan for representing non numbers, inf for representing infinite), logarithmic functions (exp(x) returns e**x), expm1(x) returns e**x-1, log2(x) returns logarithmic value for x with base2, sqrt(x) returns square root value for x), numeric functions ( factorial(x), isinf(x), remainder(x, y) returns value of remainder for dividing x by y) and trigonometric functions (sin(x), cos(x), tanx(x)).
Different Math Functions in Python
All key mathematical functions are deeply described below,
1. Constants
In the case of a mathematical constant, the value for this constant is represented by an unambiguous definition; these definitions, at some instances, are represented by means of any special symbols or by many famous mathematicians names or by any other popular means. Constants occur within numerous areas of mathematics by means of constants such as π and e happening in miscellaneous circumstances like number theory, geometry, and calculus.
The meaning of a constant to arise “naturally” and makes a constant “interesting” is in due course material of need, and a number of mathematical constants are prominent more for chronological grounds than by means for their fundamental mathematical interest. The more well-liked constants comprise been studied all the way through the ages and computed to a lot of decimal places.
| Constants | Description |
| pi | returns 3.141592 |
| E | returns 0.718282 |
| nan | Not a number |
| inf | infinite |
Example :
import math
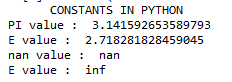
print( " CONSTANTS IN PYTHON ")
print(" PI value : " , math.pi)
print(" E value : " , math.e)
print(" nan value : " , math.nan)
print(" E value : " , math.inf)
Output :
2. Logarithmic Functions
The inverse for exponentiation is called as a logarithm. For any given number x, in order for determining its respective logarithm value, the exponent of another fixed number with base b is calculated. In a more straightforward case, the logarithm calculates or counts the numeral occurrences of the same factor in repeated multiplication;
Ex: 1000 = 10 × 10 × 10 = 103, then the “logarithm to base 10” of 1000 is 3.The logarithm of x to base b is denoted as logb (x ).
On the other hand, the exponent of a number means the number of times the number is being used in a multiplication factor.
Ex : 82 = 8 × 8 = 64
In other words, the representation of 82 could be called “8 to the power 2” or simply as “8 squared” On the other hands, the exponent of a number means the number of times the number is being used in a multiplication factor.
| Function | Description |
| exp(x) | Returns e**x |
| expm1(x) | Returns e**x – 1 |
| log(x[, base]) | x to the base logarithm is returned |
| log1p(x) | Base1 logarithm of x value is returned |
| log2(x) | Base2 logarithm of x value is returned |
| log10(x) | Base10 logarithm of x value is returned |
| pow(x, y) | Returns x raised to the power y |
| sqrt(x) | Square root value for x is returned |
Example:
import math
#variable declaration and assignation
Number_1 = 1
Number_2 = 2
Number_3 = 3
Number_4 = 4
# Applying exp() function
print(" EXPONENT VALUE ")
print(" Exponent value: " , math.exp(Number_1))
print(" \n ")
# Applying Base1 logarithm function
print(" BASE1 LOGARITHM " )
print(" BASE1 LOGARITHM VALUE of 2 : ", math.log1p(Number_2))
print(" \n " )
# Applying Base2 logarithm function
print(" BASE2 LOGARITHM " )
print(" BASE2 LOGARITHM VALUE of 2 : ", math.log2(Number_2))
print(" \n " )
# Applying Base10 logarithm function
print(" BASE10 LOGARITHM " )
print(" BASE10 LOGARITHM VALUE of 2 : ", math.log10(Number_2))
print(" \n " )
# Applying x to power of Y
print(" X^Y" )
print(" X^Y Value : ", math.pow(Number_3,Number_4))
print(" \n " )
# Applying square root determination
print(" SQUARE ROOT " )
print(" SQUARE ROOT of 4 : ", math.sqrt(Number_4))
print(" \n " )
Output :
3. Numeric Functions
The numeric functions allow the calculation of all mathematical inceptions.
| Constants | Description |
| ceil(x) | The smallest integer which is very much greater than or equal to the x value is returned |
| copysign(x, y) | Using the sign of y, the value for x is returned |
| fabs(x) | absolute value for the x is returned |
| factorial(x) | factorial value of x is returned |
| floor(x) | the largest integer, which is very much less than or equal to the x value, is returned |
| fmod(x, y) | the remainder of dividing x by y value is returned |
| frexp(x) | Returns the mantissa and exponent of x as the pair (m, e) |
| fsum(iterable) | Returns an accurate floating-point sum of values in the iterable |
| isfinite(x) | if x is not an infinity or a Nan, then boolean value true is returned |
| isinf(x) | if x holds a positive or negative infinity, then true is returned |
| isnan(x) | Returns True if x is a NaN |
| gcd(x, y) | for x and y value, the most greates common divisor value is returned |
| the remainder(x, y) | Find the remainder after dividing x by y. |
Example :
import math
#variable declaration and assignation
Number_1 = 10.5
Number_2 = 20
Number_3 = -30
Number_4 = -40.24566
Number_5 = 50
Number_6 = 60.94556
Number_7 = 70
Number_8 = 80
# Applying Ceil() function
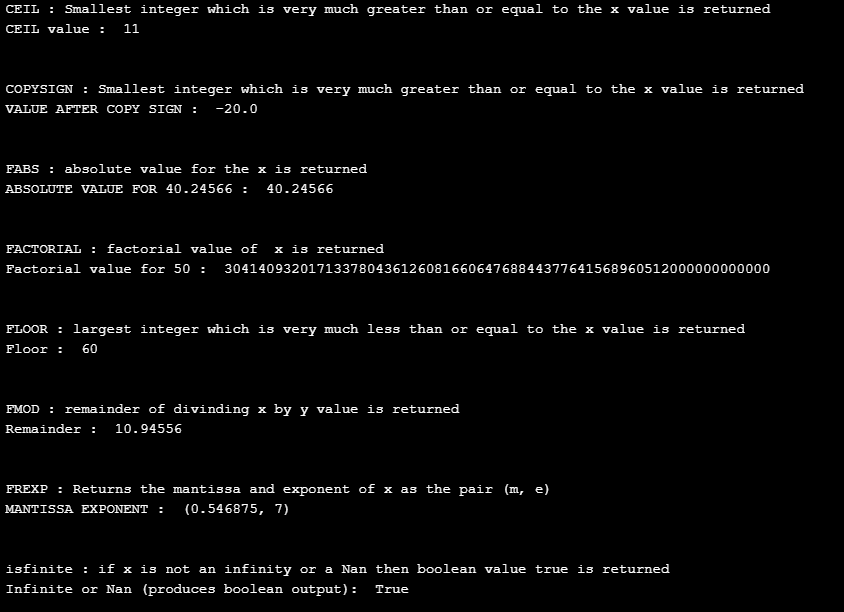
print( " CEIL : Smallest integer which is very much greater than or equal to the x value is returned ")
print( " CEIL value : " , math.ceil(Number_1))
print( " \n " )
# Applying Copysign() function
print( " COPYSIGN : Smallest integer which is very much greater than or equal to the x value is returned ")
Temp_var1 = math.copysign(Number_2,Number_3)
print(" VALUE AFTER COPY SIGN : ", Temp_var1)
print(" \n ")
# Applying fabs() function
print( " FABS : absolute value for the x is returned ")
print(" ABSOLUTE VALUE FOR 40.24566 : ", math.fabs(Number_4))
print(" \n ")
# Applying Factorial() function
print(" FACTORIAL : factorial value of x is returned ")
print(" Factorial value for 50 : ", math.factorial(Number_5))
print(" \n ")
# Applying Floor() function
print(" FLOOR : largest integer which is very much less than or equal to the x value is returned " )
print(" Floor : ", math.floor(Number_6))
print(" \n ")
# Applying Fmod() function
print(" FMOD : remainder of divinding x by y value is returned ")
print(" Remainder : ", math.fmod(Number_6,Number_5))
print(" \n ")
# Applying Frexp() function
print( " FREXP : Returns the mantissa and exponent of x as the pair (m, e) " )
print(" MANTISSA EXPONENT : ", math.frexp(Number_7))
print( " \n " )
# Applying isfinite() function
print(" isfinite : if x is not an infinity or a Nan then boolean value true is returned ")
print(" Infinite or Nan (produces boolean output): ", math.isfinite(Number_8))
print(" \n ")
# Applying gcd() function
print(" GCD : for x and y value the most greates common divisor value is returned ")
print(" Greatest Common divisor value : ", math.gcd(Number_8,Number_7))
print(" \n ")
Output:
4. Trigonometric Functions
In mathematics, trigonometric functions are used to narrate a point of view of a right-angled triangle in two side lengths. they have a very large set of applications in sciences that are relative to geometry; such include solid mechanics, celestial mechanics, navigation, a lot of others. These are considered simple periodic functions and widely known for representing the periodic phenomena from beginning to the end of Fourier analysis.
| function | Description |
| sin(x) | sine value of x in radians is determined |
| cos(x) | cosine value of x in radians need to be determined |
| tan(x) | tangent value of x in radians need to be determined |
| degrees(x) | radian to degree conversion |
| radian(x) | the degree to radian conversion |
Example :
import math
print(" \n ")
print(" TRIGNOMETRIC FUNCTION USAGE " )
print(" \n ")
print(' The value of Sin(90 degree) : ' + str(math.sin(math.radians(90))))
print(' The value of cos(90 degree) : ' + str(math.cos(math.radians(90))))
print(' The value of tan(pi) : ' + str(math.tan(math.pi)))
print(" \n ")Output :
Conclusion – Math Functions in Python
Like many other programming languages, python also offers a very diversified set of mathematical functions, which makes it a strongly implied high-level programming language in the programming arena.
Recommended Articles
This is a guide to Math Functions in Python. Here we discuss different mathematical functions in Python with examples. You can also go through our other suggested articles –