Definition of Alpha-Beta Pruning
Alpha-beta (AB) pruning is an improvised version of the Minimax algorithm. The search optimization technique employed by this pruning algorithm cuts down the spread of search and reduces the computation time considerably.
Minimax algorithm exhaustively reviews all the nodes in the search tree for maximizer turn and minimizer turn and decides the best possible course whereas AB-Pruning skips some of the branches in the search tree which yields insignificant value and penetrates to any level in the tree.
AB pruning deals with two parameters called Alpha and Beta, assigned for maximizer and minimizer respectively at each and every step of the search operation and hence the name AB-Pruning.
What is Alpha Beta Pruning?
Let’s study the AB-Pruning technique in detail.
1. Adversarial Search
Normally any search strategy is associated with a single entity and the result of this strategy will be an optimal action sequence. There may be scenarios where more than one entity will be involved in the search space with confronting intentions and they will be pitted against each other towards reaching their objectives/goals. The search strategy of each of the entity will depend on the opponent’s move and the likely impact it will bring in their pursuit towards meeting the end objectives.
Such search strategies where more than one stakeholder with competing intentions fight in the search space in reaching their goals are known as adversarial searches and it is mostly adopted in Games-like situations. This concept is used in artificial intelligence, game theory, decision theory, statistics, and philosophy fields and it is also applied in decision making in business scenarios where many uncertainties exist.
The strategies adopted by players vary according to the game situation and each one will follow different directions. One player will take the upper hand and try to maximize the gain (Maximizer) and the opponent will try to control damage and minimize the loss (Minimizer).
2. Minimax Algorithm
Minimax algorithm is built over the minimizer and maximizer concept as explained above, but it is not all that efficient and intuitive. It goes through all the nodes in the game hierarchy end to end and explores all possibilities before arriving at the final game path.
3. Improvements Over Minimax
AB Pruning algorithm is built on the fundamentals of Minimax and improvised with search optimization features. It reduces the number of nodes searched in the game hierarchy and saves time and resources. For Maximizer it computes the maximum value of minimum gain and it is stored in a parameter called Alpha and for Minimizer it computes minimum values of maximum loss and it is stored in a parameter called Beta. The values stored in Alpha and Beta decide the way the search operation is executed.
The depth of the nodes to be examined is exponentially higher in AB algorithm and it cannot be reduced but the number of nodes to be examined can be reduced drastically by eliminating the nodes that do not contribute any value to the outcome and this elimination process is called as pruning.
Functions of Alpha-Beta Pruning
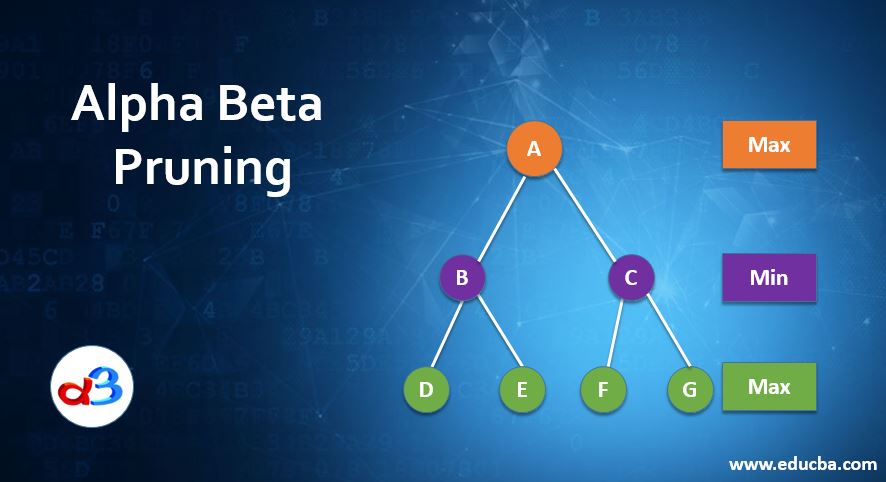
Let us examine a case of two players engaged in a search (or game) with 5 levels of nodes.
- The topmost level will be the root and it will have only one.
- The terminal level (5th level) contains leaf nodes and it will have values in all the leaves.
- Each level will either have maximizer’s turn or minimizer’s turn and it will change alternatively.
- Each node is connected by branches to another node at a level below.
- The sequence of Search operations will be from top to bottom and the left node to the right node.
- Maximizer will have its value in a parameter Alpha and Minimizer will have Beta.
- The initial value of Alpha will be -∞ (-infinity) the lowest and for the beta will be +∞ (+infinity) the highest.
- The search starts with an initial value of Alpha and Beta at the root.
- The values are propagated to the next node (if it is empty) in the one level below (left or right) following the search sequence as explained in step 5.
- If the level of the tree is Minimum turn, Beta value is compared with the values of the node in the next lower level and the Beta value is changed with the lowest value of all.
- If the level of the tree is Maximum turn, Alpha value is compared with the values of the node in the next lower level and the Alpha value is changed with the highest value of all.
- If the value of Alpha is greater than or equal to the value of Beta, the branch below will be pruned and will not be explored further. By this, the number of search operations will be brought down considerably.
- The above 4 steps (Step 9 to 12) are iterated till all the nodes at all levels other than what is pruned are explored and the best value is chosen for Maximizer and Minimizer and the results are stored in Alpha and Beta parameters.
- At the end of iteration and completion of the search, Alpha will contain the highest possible score for the maximizer and Beta will contain the lowest possible score for the minimizer.
Search Tree Hierarchy
Key Points in Alpha Beta Pruning
- Value of Alpha and Beta will be passed to the nodes down below (Child nodes) in forward.
- In backward movement in the tree, only node values will be passed on to the upper node as against Alpha and Beta values in the top to down
- Value of Alpha only will be updated in tree level assigned for
- Value of Beta only will be updated in tree level assigned for
- The order in which the nodes are examined (Search movement) is very much important to maximize the pruning and save time and effort. It’s always ideal to start from the leftmost node and move rightwards.
- The best way to arrive at a good ordering is to start from the shallowest node and check the best nodes first to improve the probability of
Recommended Articles
This is a guide to Alpha Beta Pruning. Here we also discuss the definition and working of alpha beta pruning along with features. You may also have a look at the following articles to learn more –