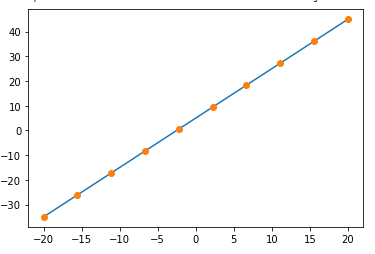Updated April 3, 2023
Introduction to NumPy polyfit
In python, Numpy polyfit() is a method that fits the data within a polynomial function. That is, it least squares the function polynomial fit. For example, a polynomial p(X) of deg degree fits the coordinate points (X, Y). This function returns a coefficient vector p that lessens the squared error in the deg, deg-1,…0 order. However, a RankWarning is issued by polyfit when the fit of the least-squares is poorly conditioned. This means that, as a result of numerical error, the best fit is not properly defined. The outcome can be enhanced by replacing x with x-mean(x) or minimizing the polynomial degree.
Syntax and parameters of NumPy polyfit
Below is the syntax of the polyfit method in numpy.
numpy.polyfit( x , y , deg , rcond = None , full = False, w = None, cov = False)Parameters:
- x: This parameter is array-like which is of the shape of (M,) size.
– Represents the M sample x-coordinate value of (x[i], y[i]).
- y: This parameter is array-like which is of the shape of (M,) or (M, K) size.
– Represents the M sample y-coordinate value of (x[i], y[i]).
- Deg: int value which is the fitting polynomial degree.
- rcond: float value which is considered as optional.
-This parameter represents the relative condition value of the fit.
– Singular numbers that are less than this relative condition to the highest singular value can be avoided.
-len(x)*ep is the default value of rcond.
-Here, ep is the relative precision of the type float.
-In most cases, 2e-16 is the value.
- full: A boolean value which is optional
-This is considered as a switch that is responsible for the nature of value returned.
-If the value is false, it returns the coefficients.
– If the value is true, it returns the diagnostic data from the singular value decomposition.
- w: This parameter is array-like which is of the shape of (M,) size.
-This parameter weights to put to the sample point’s y-coordinates.
-In the case of Gaussian uncertainties, 1/sigma has to be used instead of 1/sigma**2
- cov: A boolean value which is optional
-This parameter returns the estimate as well as the estimated covariance matrix.
-If the value of full is true, this parameter won’t return.
Return value:
- p: This parameter is an ndarray which is of shape ( deg + 1, ) or ( deg + 1,K)
-This is the polynomial coefficient which has the highest power mentioned first.
– If the value of y is 2-dimensional, the kth dataset coefficient will be set as p[:,k].
- Moreover, the list [residuals, rank, singular_values, rcond] will be returned only if the value of full is true. Here, residuals are the residual of the least square fit; Rank is the scaled vandermonde coefficient matrix rank, singular value, and the value of rcond.
- V: This value is a ndarray which is of shape M, M) or (M, M, K).
– This value will be returned only if the value of full is false and the value of cov is true.
– Polynomial coefficient estimates’ covariance matrix.
How polyfit function work in NumPy?
Now, let us see how to fit the polynomial data with the help of a polyfit function from the numpy standard library, which is available in Python.
Assume that some data is available in the polynomial. This is to use the function polyfit() for fitting the data available in the polynomial.
A polynomial with a degree of 1 is the simplest known polynomial.
It is mentioned using the equation y=m*x+c
Similar to that, the degree 2 quadratic equation is denoted by the equation
Y = ax**2 + bx + cIn this case, the polyfit method will find all the m, c coefficients for degree 1. This will calculate the a, b, and c coefficients for degree 2.
Below is a sample code for a simple line.
Code:
import matplotlib.pyplot as mp
import numpy as np
x = np.linspace( -10 , 10 , 5 )
y = 2*x + 5
mp.plot( x , y , 'o' )If the function polyfit() is also added, code changes as shown below.
import matplotlib.pyplot as mp
import numpy as np
x = np.linspace( -10 , 10 , 5 )
y = 2*x + 5
coeff = np.polyfit(x,y,2)
xn = np.linspace(-20,20,100)
yn = np.poly1d(coeff)
mp.plot( xn,yn(xn),x,y,'o')Note:
In some cases, fitting polynomial coefficients is intrinsically badly conditioned. For example, it is during the cases when the polynomial degree is higher or the interval of sample points is poorly centered. Moreover, the quality of the fit has to be always checked in the cases mentioned above. If the polynomial fits are not that satisfactory, a good alternative will be splined.
Examples of NumPy polyfit
Let us look into more examples of polyfit function in numpy:
Example #1
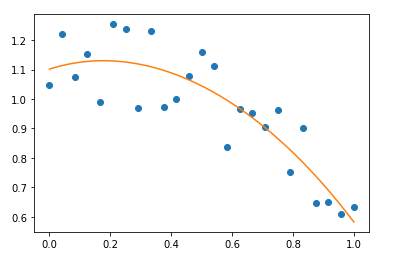
Python program to fit a polynomial function
Code:
import numpy as np
import matplotlib.pyplot as mp
np.random.seed(12)
x = np.linspace( 0, 1, 25 )
y = np.cos(x) + 0.3*np.random.rand(25)
p = np.poly1d( np.polyfit(x, y, 4) )
t = np.linspace(0, 1, 250)
mp.plot(x, y, 'o', t, p(t), '-')
mp.show()Output:
In this program, first, import the libraries matplotlib and numpy. Set the values of x, y, p, and t. Then, using the values of this x, y, p, and t, plot the polynomial by fitting it.
Example #2
Python program to fit a polynomial function of a simple line
Code:
import numpy as np
import matplotlib.pyplot as mp
np.random.seed(12)
x=np.linspace(-20,20,10)
y=2*x+5
coeff = np.polyfit(x,y,2)
xn = np.linspace(-20,20,100)
yn = np.poly1d(coeff)
mp.plot( xn,yn(xn),x,y,'o')Output:
In this program, also, first, import the libraries matplotlib and numpy. Set the values of x and y. Then, calculate the polynomial and set new values of x and y. Once this is done, fit the polynomial using the function polyfit().
Conclusion
Numpy polyfit() is a method available in python that fits the data within a polynomial function. Here, it least squares the function polynomial fit. That is, a polynomial p(X) of deg degree is fit to the coordinate points (X, Y). In this article, different aspects such as syntax, working, and examples of polyfit() function are explained in detail.
Recommended Articles
This is a guide to NumPy polyfit. Here we discuss How polyfit functions work in NumPy and Examples with the codes and outputs. You may also have a look at the following articles to learn more –