Updated March 3, 2023

Introduction to Moving Average Matlab
In mathematics, the central value is called ‘average’ while in statistics is known as mean. The “mean” or “average” we are used to, where we add up all the numbers include in the input argument and then divide that all numbers by a total count of that number. In Matlab to calculate a moving average “movmean” statement is used. A moving average is commonly using along with time-series input data and the parameters of the moving average will be set according to application. If input arguments are a vector, then movmean operates along the length of the vector. If the input argument is a multidimensional array, then movmean operates along the first array dimension whose size does not equal 1.
Syntax
The syntax for Moving Average Matlabisas shown below:-
- M1 = movmean(A1,k1)
- M1 = movmean(A1,[kb kf])
- M1 = movmean(___,dim1)
- M1 = movmean(___,nanflag)
- M1 = movmean(___, Name, Value)
How to Find moving Average in Matlab?
In Matlab ‘movmean’ function is used to calculate the moving average. For finding the moving average of the input argument, we need to take all elements into a variable and use proper syntax.
The steps to calculate the moving average using ‘movmean’ statement:-
Step 1: We need to take all elements into a variable.
Step 2: Then we use a ‘movmean’ statement with proper syntax for find moving average.
Examples
Here are the following examples mention below:
Example #1
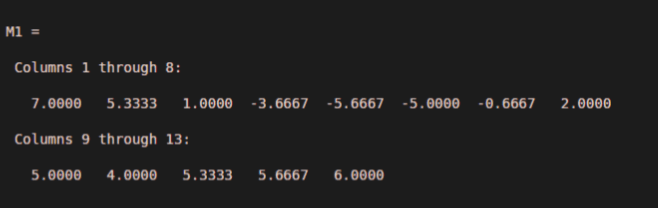
In this example we take A1 as [5 9 2 -8 -5 -4 -6 8 4 3 5 8 4] and then use a movmean syntax so we take M1 = movmean (A1, 3), the movmean gives an array of local 3 points mean values, where every mean was calculated over a sliding window of length 3 across neighboring elements of A1. When 3 are odd, the window is centered on the element in the current position. When 3 are even, the window is centered on the current and previous elements. When the window is trim, the average is taken over only for the elements that fill the window. M1 is the same size as A1.So the movmean basically adds the three neighboring elements in A1 and then the sum is divided by 3. Take the example we take 8 4 3 elements in A1, 8+4+3=15, 15/3=5 so in the output array the place at which 4 is present in A1 that place we get 5 in M1. And we have seen the result on the command window.
Code:
clc;
clear all;
close all;
A1 = [5 9 2 -8 -5 -4 -6 8 4 3 5 8 4];M1 = movmean(A1,3)
Output:
Example #2
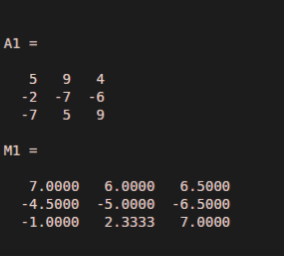
In this example, we take a 3*2 matrix and this matrix is stored in the A1 variable, and this 3 by 2 matrix is passed through the movmean function. For a matrix we use a command like movmean (A1, 3, 2), basically, this is a syntax for that command movmean(___,dim1) returns the array of moving averages along dimension dim1 for any of the previous syntaxes. In our example, if A1 is a matrix, then movmean(A1, 3,2) operates along with the columns of A1, computing the 3 element sliding mean for each row. But the first and last element in a row we take just 2 numbers, and we take that average or mean. The output matrix is also the same dimensions as input 3*2 matrixes.
Code:
clc;
clear all;
close all;
A1 = [5 9 4; -2 -7 -6; -7 5 9]
M1 = movmean(A1,3,2)
Output:
Example #3
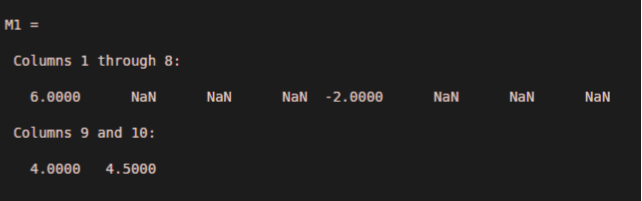
Let us see an example, in this example, we take a one-row vector and that row vector we stored in the A1 variable. In that vector along with numbers, we take a NaN value. And then using a movmean function we take a moving average of that numbers. We put the value of k as 3, so the command is like M1 = movmean (A1, 3)the movmean returns an array of local 3 points mean values, where every mean was calculated over a sliding window of length 3 across neighboring elements of A1. But if NaN is taking for calculating the mean then the output is also NaN. So now we recalculate the average but omit the NaN values. When movmean reject NaN elements, it requires the average over the remaining elements in the window. So for this, we take command as Movmean (A1, 3, ‘omit an’).
Code:
clc;
clear all;
close all;
A1 = [4 8 NaN -1 -2 -3 NaN 3 4 5];M1 = movmean(A1,3)M1 = movmean(A1,3,'omitnan')
Output:
Conclusion – Moving Average Matlab
In this article, we saw the concept of moving average in MatLab. Basically moving average is used to calculate the average of 3 neighboring elements from the input. Then saw syntax related to moving average statements and how it is used in Matlab code. Also, we saw some examples related to moving average statement.
Recommended Articles
This is a guide to Moving Average Matlab. Here we discuss How to Domoving Average Matlab and Examples along with the codes and outputs. You may also have a look at the following articles to learn more –