Updated April 5, 2023

Introduction to Smith Number
Smith number is defined as a recreational mathematics number in a number series that has to be a composite number, and the digits in the prime factors of the number sum up to being equal to the sum of the digits in the number itself. Thus, in the example of number = 121, since the sum of the digits in the original number and the digits in the prime factor are the same, we call the number as Smith number. Try doing it with another number of your choice. Albert Wilansky introduced this number after he found this pattern in the telephone number of his brother-in-law.
Logic Behind Smith Number
- We will see the logic using an example if the number is 121, it satisfies the condition that 121 is a composite number, now the sum of the digits is equal to 1 + 2 + 1 = 4, and the prime factors of the number are 11 and 11 as 1, and 121 is not a prime number. Even if the number is a square, we need to take the same number twice. Now the sum of the prime factors (11 and 11) is 1 + 1 + 1 + 1 = 4.
- The code implementation tries to test the entire logic by breaking it down into writing the logic of testing prime, the sum of the prime factors, and some of the digits in the number. Now using the below step-by-step algorithm, let us understand it theoretically and then implement it into respective.
How to Check Smith Number?
Let’s see at the step by step process:
We will go through the pseudocode here and then use it to implement it into C++/Python/Java.
- First, take the number as an input.
- Using the concept of finding the last digit, we keep summing up the digits one by one to finally return the sum and store it into a variable.
- Now, we define another function to check for a number being prime.
- Now, another function is written to find the factors, check for the factors to be prime, and if true, then keep summing those up.
- Finally, this sum of prime factors is returned.
- The 2 sums are then compared to return a true or false of checking the number entered being Smith number.
Examples of Smith Number
Different examples are mentioned below:
Example #1
Finding Smith number in C++.
Syntax:
#include <iostream>
#include<math.h>
using namespace std;
int findSumOfDigit(int n) {
int s = 0;
while (n > 0) {
s = s + n % 10;
n = n / 10;
}
return s;
}
bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
int findSumPrimeFactors(int n) {
int i = 2, sum = 0;
while (n > 1) {
if (n % i == 0) {
sum = sum + findSumOfDigit(i);
n = n / i;
} else {
do {
i++;
}
while (!isPrime(i));
}
}
return sum;
}
bool isSmithNum(int num)
{
if (isPrime(num)){
return false;
}
int a = findSumOfDigit(num);
int b = findSumPrimeFactors(num);
return (a==b);
}
int main(void)
{
int num;
char choice;
do{
cout << "Enter the number you want to check for being the Smith number\n";
cin >> num;
if (isSmithNum(num))
cout << "The number you have entered is a smith number\n";
else
cout << "The number you have entered is NOT a smith number\n";
cout << "Do you want to continue to enter another number (y/n)...\n";
cin >> choice;
}while(choice=='y' || choice =='Y');
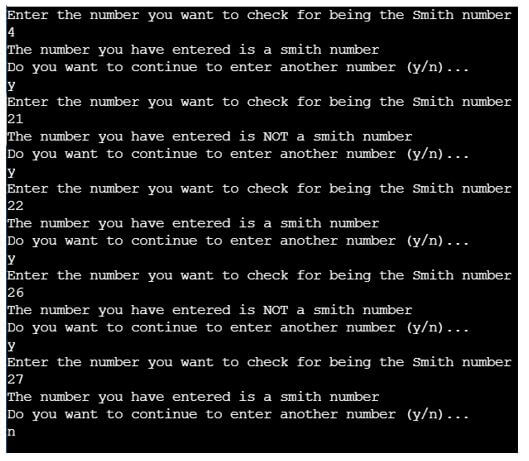
}Output:
Example #2
Finding in Python.
Syntax:
def countOfDigits(num):
c = 0
while num != 0:
num = num//10
c += 1
return c
def sumOfDigits(num):
temp = num
sum = 0
for i in range(countOfDigits(num)):
sum+=num%10
num//=10
return sum
def checkPrime(num):
for i in range(2,num):
if (num % i) == 0:
return False
else:
continue
return True
#Function to check whether a number is a Smith Number or not
def isSmithNum(num):
if(checkPrime(num)):
print("***The number you entered is prime, hence can't be a smith number***")
else:
factorizePrime = []
temp = num
c = 2
while(temp>1):
if(temp%c == 0 and checkPrime(c)):
factorizePrime.append(c)
temp/=c
else:
c+=1
continue
for i in range(0,len(factorizePrime)):
if(countOfDigits(factorizePrime[i])>1):
while(countOfDigits(factorizePrime[i])>1):
factorizePrime[i] = sumOfDigits(factorizePrime[i])
if(sum(factorizePrime) == sumOfDigits(num)):
return True
else:
return False
choice ='y'
while(choice=='y' or choice =='Y'):
print("Enter the number you want to check for being the Smith number")
num = int(input())
if (isSmithNum(num)):
print("The number you have entered is a smith number")
else:
print("The number you have entered is NOT a smith number")
print("Do you want to continue to enter another number (y/n)...")
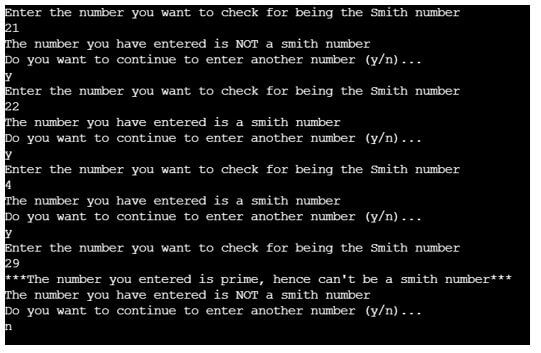
choice = input()Output:
Example #3
Finding in Java (Make sure to name the file as Main.py).
Syntax:
import java.util.*;
public class Main {
int sumOfDigits(int n) {
int s = 0;
while (n > 0) {
s = s + n % 10;
n = n / 10;
}
return s;
}
boolean checkPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
int sumOfPrimeFactors(int n) {
int i = 2, sum = 0;
while (n > 1) {
if (n % i == 0) {
sum = sum + sumOfDigits(i);
n = n / i;
} else {
do {
i++;
}
while (!checkPrime(i));
}
}
return sum;
}
boolean isSmithNum(int num)
{
if (checkPrime(num)){
System.out.println("***The number you entered is prime, hence can't be a smith number***");
return false;
}
int a = sumOfDigits(num);
int b = sumOfPrimeFactors(num);
return (a==b);
}
public static void main(String args[])
{
int n;
char choice;
Main obj = new Main();
Scanner sc= new Scanner(System.in);
do{
System.out.println("Enter the number you want to check for being the Smith number");
n= sc.nextInt();
if (obj.isSmithNum(n))
System.out.println("The number you have entered is a smith number");
else
System.out.println("The number you have entered is NOT a smith number");
System.out.println("Do you want to continue to enter another number (y/n)...");
choice= sc.next().charAt(0);
}while(choice=='y' || choice =='Y');
}
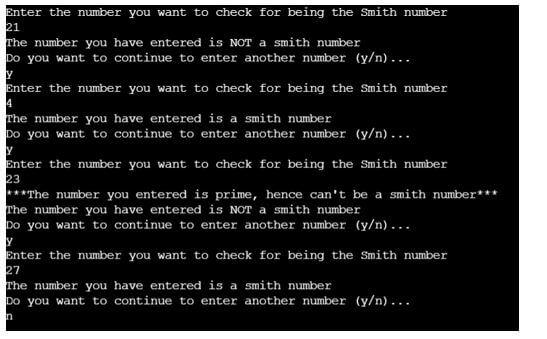
}Output:
Conclusion
In this article, we have looked at the logic and implementation. One should eye on the implementation of different functions in C++, Python, and Java, as we have tried to put down various algorithms to achieve the same result. One can try to interchange them in their own programming language as per convenience.
Recommended Articles
We hope that this EDUCBA information on “Smith Number” was beneficial to you. You can view EDUCBA’s recommended articles for more information.