Updated September 14, 2023
Introduction to Digital Signal Processing (DSP)
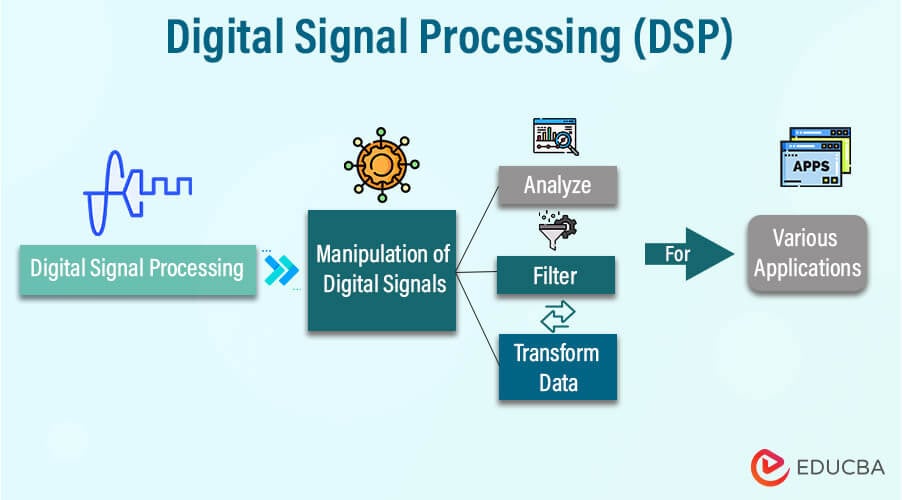
Digital Signal Processing (DSP) refers to the systematic manipulation, analysis, and transformation of digital signals, which are discrete-time representations of various data types such as audio, images, and sensor measurements.
Digital Signal Processing (DSP) is the scientific and engineering field focused on altering, analyzing, and interpreting signals. Like audio or sensor data, signals are digitized and manipulated using computational techniques.
DSP finds wide application in diverse fields, including telecommunications, audio and image processing, medical diagnostics, and more. Fundamental operations include filtering to eliminate noise, Fourier analysis to reveal frequency components, and modulation for data transmission.
DSP’s impact is pervasive, powering technologies like smartphones, medical imaging devices, and wireless communication systems, enhancing our ability to understand, transmit, and manipulate various data types with precision and efficiency.
Table of Content
- Introduction to Digital Signal Processing (DSP)
- Components Inside a Digital Signal Processor (DSP)
- Analog-to-digital conversion (ADC)
- Digital Filters and their Types
- Discrete Fourier Transform (DFT)
- Fast Fourier Transform (FFT)
- Sampling and Reconstruction
- Z transform in digital signal processing
- Digital signal processing Reddit
- fir and iir filters in digital signal processing
- Multirate digital signal processing
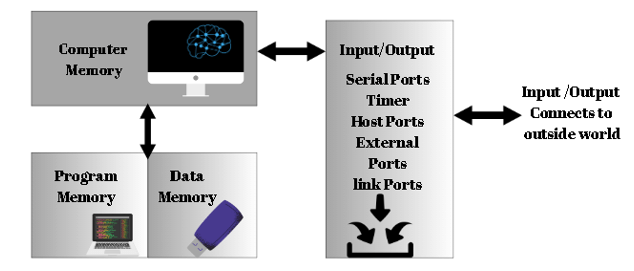
Components Inside a Digital Signal Processor (DSP)
A DSP Contains the following components; let us see them one by one
- Program Memory: This memory section stores the instructions or program code the DSP will execute. It includes the sequence of operations needed to process the data effectively.
- Data Memory: Data memory is where the input data to be processed, intermediate results, and output data are stored during the DSP’s operations. Efficient data memory management is crucial for optimizing data movement and access times, especially for real-time processing.
- Compute Engine: The compute engine is the heart of the DSP. It includes various functional units such as the Arithmetic Logic Unit (ALU) and Multiplier-Accumulator (MAC) unit. The ALU performs basic arithmetic and logic operations, while the MAC unit specializes in the multiply-accumulate operation, which is central to many signal processing algorithms.
- Input/Output Interfaces: The input/output (I/O) interfaces connect the DSP and the external world. These interfaces include analog-to-digital converters (ADCs) to convert analog signals into digital format for processing and digital-to-analog converters (DACs) to convert processed digital signals into analog form.
- Control Unit: The control unit manages the execution of instructions fetched from the program memory. It coordinates the data flow between various components, controls the sequence of operations, and ensures that the DSP operates according to the programmed algorithm.
Combining these critical components enables the DSP to process digital signals efficiently.
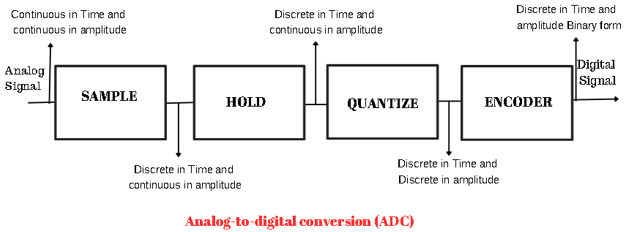
Analog-to-Digital Conversion (ADC)
Analog-to-digital conversion (ADC) is a crucial digital signal processing process involving converting continuous analog signals into discrete digital signals. This process allows analog signals, such as audio, video, temperature readings, and sensor measurements, to be processed and manipulated using digital techniques.
Here’s how the ADC process works:
- Sampling: The first step is to sample the continuous analog signal regularly. This involves measuring the amplitude of the analog signal at specific time points. The sampling rate is the frequency at which samples are taken.
- Quantization: The sampled analog values are then quantized, which means they are approximated to a specific number of discrete levels. This quantization introduces a level of granularity into the digital representation of the signal. The bit depth of the ADC determines the number of quantization levels.
- Encoding: After quantization, each sample is encoded as a binary number. The bit depth of the ADC determines the number of bits used to represent each sample.
- Conversion: The encoded binary values are now digital and can be processed by digital systems such as computers or microcontrollers. This allows for various digital signal processing operations like filtering, modulation, and analysis.
The quality of the digital representation depends on the sampling rate (how frequently samples are taken) and the bit depth (the number of bits used to represent each sample).
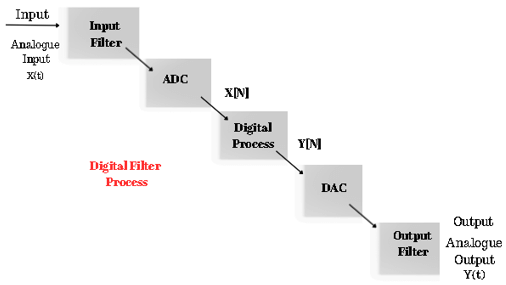
Digital Filters and their Types
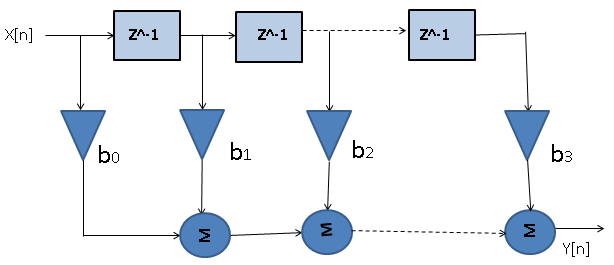
Digital filters are crucial tools in digital signal processing that alter a signal’s frequency content. They come in two main types: Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters.
FIR filters have a finite duration impulse response, making each output a weighted sum of input samples. They offer precise control over characteristics and linear phase response, making them ideal for applications like audio equalization.
IIR filters have an infinite duration impulse response involving input and previous output samples in their calculations. They are computationally efficient and used when efficiency matters, such as in audio effects.
Both filter types can be further categorized based on their frequency responses: low-pass, high-pass, band-pass, and band-stop filters. They serve applications ranging from noise reduction to audio effects.
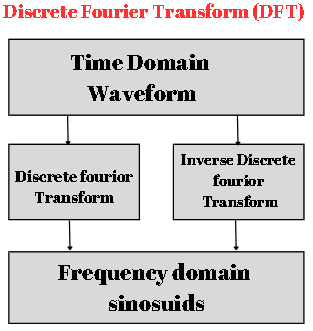
Discrete Fourier Transform (DFT)
The Discrete Fourier Transform (DFT) is a fundamental tool in digital signal processing that analyzes and transforms a discrete-time signal from the time domain into the frequency domain. It decomposes a signal into its constituent sinusoidal components, revealing the frequencies and magnitudes present.
Mathematically, the DFT computes complex numbers representing the amplitudes and phases of various sinusoids that construct the signal. The result is a spectrum depicting the frequency components present in the signal. The Fast Fourier Transform (FFT) is a widely used algorithm to compute the DFT.\ efficiently.
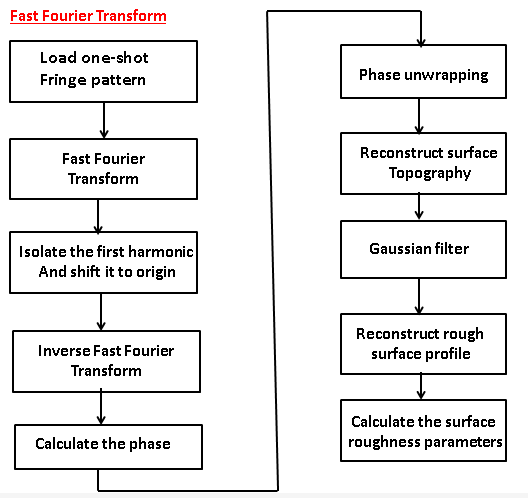
Fast Fourier Transform (FFT)
The Fast Fourier Transform (FFT) is a widely used algorithm for efficiently computing a discrete-time signal’s Discrete Fourier Transform (DFT). It significantly reduces the computational complexity of the DFT, making it practical for real-time and high-speed applications.
The FFT exploits the inherent symmetries and periodicities in the calculation of the DFT to minimize the number of computations required. It breaks down the DFT into smaller sub-problems by recursively dividing the input signal into even and odd components. This divide-and-conquer approach dramatically reduces the number of multiplications and additions compared to the direct computation of the DFT.
The FFT algorithm revolutionized signal processing, allowing rapid spectral analysis of signals. It’s crucial in applications such as audio processing, image compression, communication systems, and scientific simulations.
Sampling and Reconstruction
Sampling converts a continuous-time analog signal into a discrete-time digital signal by taking measurements at regular intervals. It involves capturing the analog signal’s amplitude at specific time instances, creating a sequence of discrete values. The sampling rate determines how frequently these measurements are taken.
Reconstruction is converting a discrete-time digital signal back into a continuous-time analog signal. This is achieved using interpolation techniques to reconstruct intermediate values between the discrete samples.
Sampling is the initial step for processing analog signals in digital systems. At the same time, reconstruction is vital when converting the processed digital signal back to an analog format for output or visualization.
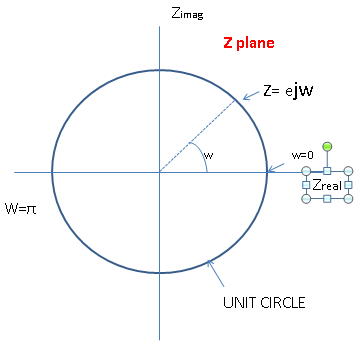
Z transform in Digital Signal Processing
The Z-transform is a mathematical tool used in digital signal processing to analyze and manipulate discrete-time signals and systems in the frequency domain.
Similar to the Laplace transform for continuous signals, the Z-transform provides a way to represent discrete signals and systems in a complex plane. It’s beneficial for analyzing discrete systems’ stability, transient response, and frequency characteristics.
The Z-transform converts a discrete signal sequence into a function of a complex variable, “z,” allowing signals and system behaviors to be studied algebraically. It plays a crucial role in designing filters, analyzing digital control systems, and understanding the behavior of discrete systems.
Digital Signal Processing Reddit
Reddit is a popular online platform where users can engage in discussions, share information, and participate in various communities based on their interests. There is a subreddit dedicated to Digital Signal Processing where people interested in this field can connect, ask questions, share knowledge, and discuss related topics.
To find this subreddit, visit Reddit’s website or app and search for “r/DSP” in the search bar. Remember that Reddit communities (subreddits) can vary in terms of activity and content quality, so it’s a good idea to read through some posts and comments to get a sense of the community before engaging.
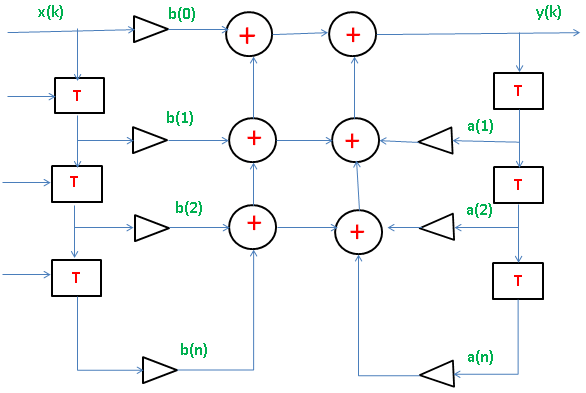
FIR and IIR Filters in Digital Signal Processing
Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters are two main types of digital filters used in digital signal processing (DSP) for various applications:
FIR Filters (Finite Impulse Response):
FIR filters have a finite-duration impulse response, meaning their output is based solely on a finite number of input samples. Each output sample is a weighted sum of a finite number of input samples.
IIR Filters (Infinite Impulse Response):
IIR filters have an impulse response that extends indefinitely but with decreasing amplitudes. Each output sample depends on both input samples and previous output samples.
| Aspects | FIR Filters (Finite Impulse Response): | IIR Filters (Infinite Impulse Response): |
| Advantages |
|
|
| Application | Audio and image processing
Communication systems System identification Equalization |
Audio effects (reverb, echo)
Biomedical signal processing Control systems Communication systems |
Choosing between FIR and IIR filters depends on the desired frequency response, phase linearity, computational resources, and stability requirements.
FIR filters are preferred for applications that demand precise control over characteristics and linear phase response.
IIR filters are chosen for efficiency and when computational resources are limited, but they require careful stability consideration.
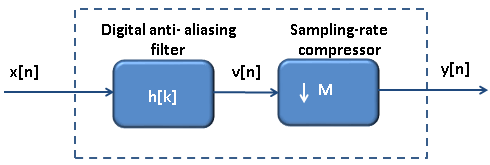
Multirate Digital Signal Processing
Multirate digital signal processing involves manipulating digital signals at multiple sampling rates.
It includes decimation (reducing sampling rate), interpolation (increasing sampling rate), and techniques like filter banks and polyphase decomposition to process signals efficiently.
This approach optimizes computational resources, conserves bandwidth, and accommodates different processing needs within a system. Applications range from audio processing, where it improves efficiency in other frequency bands, to telecommunications and image compression, where it adapts to varying data rates and enhances resource allocation. Multirate DSP enables adaptive and resource-efficient signal processing in diverse fields.
FAQs of Digital Signal Processing
Q1. What is digital signal processing (DSP)?
Answer: DSP is manipulating, analyzing, and transforming digital signals to extract, enhance, or modify information.
Q2. What’s the significance of DSP in real-world applications?
Answer: DSP is crucial in various fields, including telecommunications, audio processing, medical imaging, and more. It enables us to analyze, filter, and interpret digital signals, enhancing communication, entertainment, and scientific understanding.
Q3. What’s the difference between analog and digital signals?
Answer: Analog signals are continuous voltage or current variations, while digital signals are discrete values representing information. DSP transforms analog signals into digital form for processing.
Q4. How does sampling relate to DSP?
Answer: Sampling is the process of converting continuous analog signals into discrete digital values. DSP works with these discrete samples to analyze and manipulate signals.
Q5. What’s the role of multirate signal processing?
Answer: Multirate processing involves manipulating signals at multiple sampling rates. It optimizes resource usage, conserves bandwidth, and adapts to varying processing requirements.
Q6. How do digital filters remove noise from signals?
Answer: Digital filters attenuate undesired frequency components, effectively reducing noise while preserving the relevant signal information.
Conclusion
In conclusion, Digital Signal Processing (DSP) is a vital field enabling the analysis and manipulation of digital signals. It revolutionizes industries by converting analog to digital, utilizing FFT for frequency insights, employing filters for enhancement, and optimizing efficiency through multi-rate processing. DSP’s influence spans communication, healthcare, and technology sectors.
Recommended Articles
We hope that this EDUCBA information on “Digital Signal Processing” was beneficial to you. You can view EDUCBA’s recommended articles for more information,