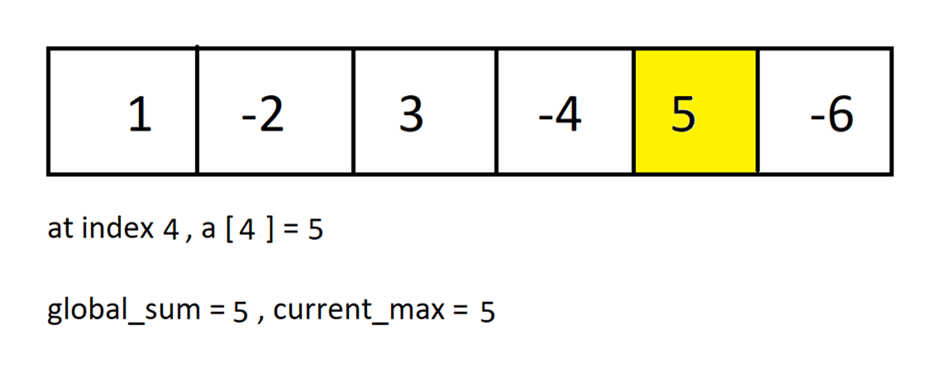Updated December 21, 2023
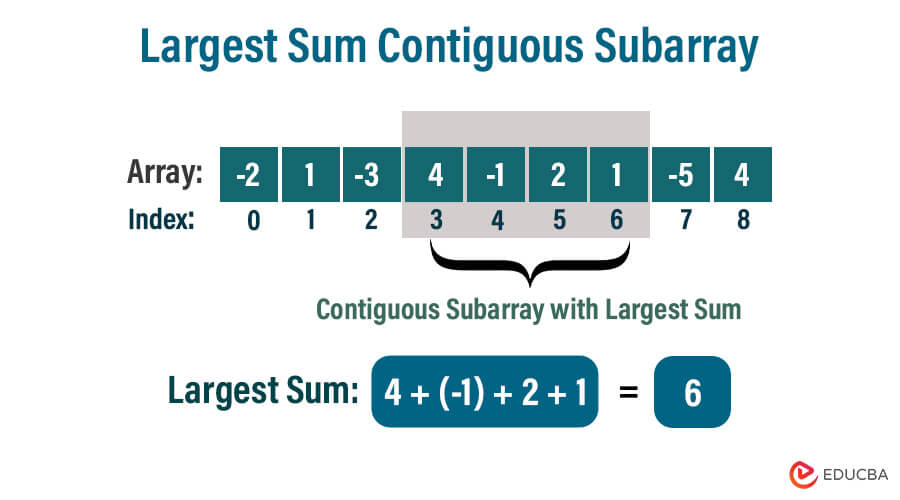
Introduction to Largest Sum Contiguous Subarray
The most significant sum contiguous array is a topic that involves determining the most important sum of consecutive arrays. We will dive into the most popular techniques and algorithms like Kadane’s algorithm, the Brute force approach, the divide and conquer method, etc. We are considering time and space complexities and Real-world scenarios. Each technique is unique and has its pros and cons. We will apply these techniques using multiple programming languages for better understanding.
Table of Contents
- Introduction
- Kadane’s Algorithm
- Dynamic Programming
- Brute Force Approach
- Divide and Conquer Approach
- Comparison of Time and Space Complexities
Key Takeaways
- Determines the most significant sum by tracking start and end indices.
- Covers applications like image and signal processing, ML, etc.
- Maintains its robustness with a simple approach and precise result regardless of the array’s element, size, and complexity.
- Kadane’s algorithm provides an optimized solution for extreme conditions. It has a space complexity of 0(1).
Kadane’s Algorithm
Kadane’s algorithm is a dynamic programming algorithm that efficiently finds the most enormous sum contiguous array. It has linear time complexity 0(n).
Steps:
- Define two variables: global_sum ( used to store the maximum sum of the subarray so far ) and current_max ( used to keep the total sum of the subarray till the current item of the array ).
- Initially, set both to 0.
- Iterate through arrays. If the first element exceeds 0, simply assign ( global_sum and current_max ) with that value.
- Go to the next element of the array[i]. Update the value of current_max to the maximum of array[i] and the sum of current_max and array[i].
- Update the value of global_sum if and only if its value is less than the value of current_max.
- Follow these steps with all the elements of the array. And the final global_sum is our most considerable sum contiguous subarray.
Implementation
Let us convert all the above theories into Implementation for better understanding.
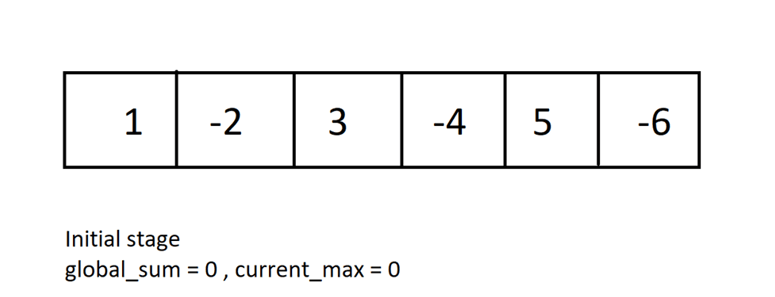
Picture an array = [ 1, -2, 3, -4, 5, -6 ]
global_sum = 0.
current_max = 0.
Step 1: At index 0, we have element “1”. Since one is greater than 0, update
current_max = 1.
global_sum = 1.
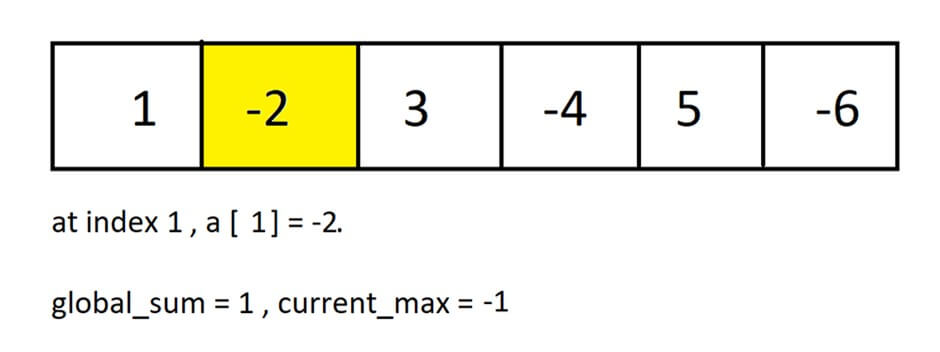
Step 2: At index 1, we have the element “-2”.
a ( addition of current_max and current element of the array ) = 1 + (-2) = 1 – 2 = -1
b ( current element of the array ) = -2
Since a is greater than b ( -1 > -2 ), update
current_max = -1.
global_sum = 1. ( global_sum remains unchanged because, at step 1, it has value 1, which is greater than current_max )
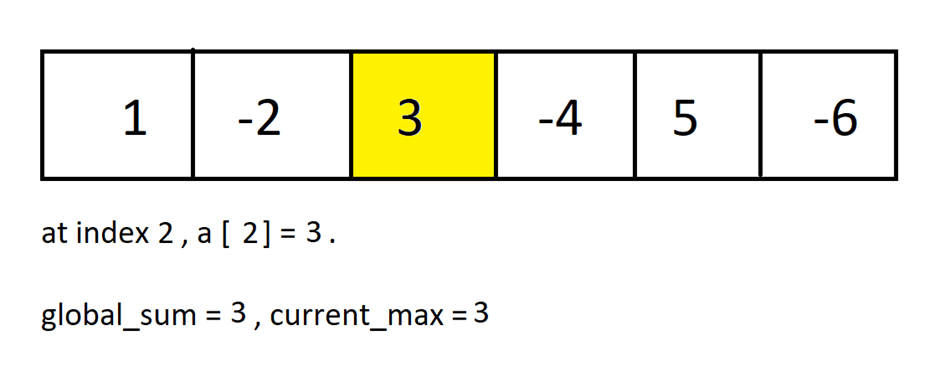
Step 3: At index 2, we have the element “3”.
a ( addition of current_max and current element of the array ) = -1 + (3) = 3 – 1 = 2
b ( current element of the array ) = 3.
Since a is less than b ( 2 < 3 ), update
current_max = 3.
global_sum = 3. ( global_sum will change because, at step 2, it has value 1, which is less than current_max )
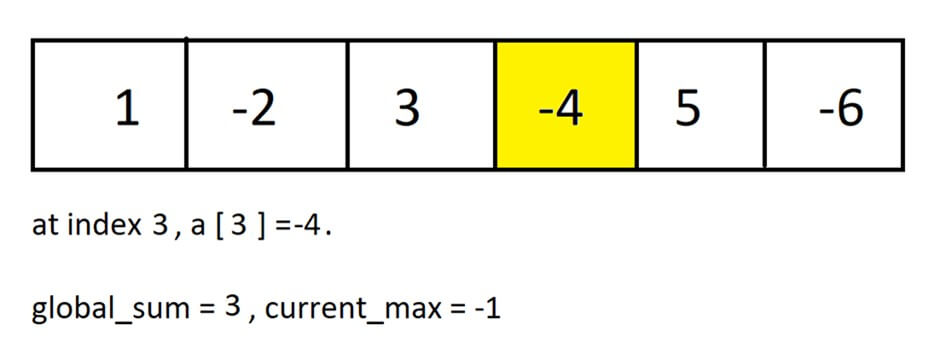
Step 4: At index 3, we have the element “-4”.
a ( addition of current_max and current element of the array ) = 3 + (-4) = 3 – 4 = -1
b ( current element of the array ) = -4.
Since a is greater than b ( -1 > -4 ), update
current_max = -1.
global_sum = 3. ( global_sum will remain unchanged because, at step 3, it has value 3, which is greater than current_max )
Step 5: At index 4, we have the element “5”.
a ( addition of current_max and current element of the array ) = -1 + (5) = 5 – 1 = 4
b ( current element of the array ) = 5.
Since a is less than b ( 4 < 5 ), update
current_max = 5.
global_sum = 5. ( global_sum will change because, at step 4, it has value 3, which is less than current_max )
Step 6: At index 5 (last element), we have the element “-6”.
a ( addition of current_max and current element of the array ) = 5 + (-6) = 5 – 6 = -1
b ( current element of the array ) = -6.
Since a is more significant than b ( -1 > -6 ), update
current_max = -1.
global_sum = 5. ( global_sum will remain unchanged because, at step 5, it has value 5, which is greater than current_max )
Hence, we get the Output, Largest Sum Contiguous Subarray = global_sum = 5.
Tabular representation
array = [ 1, -2, 3, -4, 5, -6 ]
global_sum = 0.
current_max = 0.
| current_max | global_sum |
| 1 | 1 |
| -1 | 1 |
| 3 | 3 |
| -1 | 3 |
| 5 | 5 |
| -1 | 5 |
Hence, we get the Output, Largest Sum Contiguous Subarray = global_sum = 5.
Print Largest Sum Contiguous Subarray
Let us print the largest sum of contiguous subarrays using Kanade’s algorithm with different programming languages.
Array = [1,-2,3,-4,5,-6]
1. Implementation using C++
Code:
#include <bits/stdc++.h>
using namespace std;
int maxSumOfSubArray(int a[], int array_size) {
int global_sum = INT_MIN, current_max = 0;
for (int x = 0; x < array_size; x++) {
current_max = current_max + a[x];
if (global_sum < current_max)
global_sum = current_max;
if (current_max < 0)
current_max = 0;
}
return global_sum;
}
int main() {
int a[] = {1, -2, 3, -4, 5, -6};
int n = sizeof(a) / sizeof(a[0]);
int max_sum = maxSumOfSubArray(a, n);
cout << "Using C++ Largest sum contiguous subarray is " << max_sum << endl;
return 0;
}Output:
2. Implementation using Java
Code:
public class Main {
static int maxSumOfSubArray(int[] a, int size) {
int global_sum = Integer.MIN_VALUE;
int current_max = 0;
for (int x = 0; x < size; x++) {
current_max = current_max + a[x];
if (global_sum < current_max) {
global_sum = current_max;
}
if (current_max < 0) {
current_max = 0;
}
}
return global_sum;
}
public static void main(String[] args) {
int[] a = {1, -2, 3, -4, 5, -6};
int n = a.length;
int max_sum = maxSumOfSubArray(a, n);
System.out.println("Using Java Maximum contiguous sum is " + max_sum);
}
}Output:
3. Implementation using Python
Code:
def maxSumOfSubArray(arr):
global_sum = float('-inf')
current_max = 0
for num in arr:
current_max += num
if global_sum < current_max:
global_sum = current_max
if current_max < 0:
current_max = 0
return global_sum
if __name__ == "__main__":
a = [1, -2, 3, -4, 5, -6]
max_sum = maxSumOfSubArray(a)
print("Using Python Maximum contiguous sum is ", max_sum)Output:
Real-World Applications
- Finance – Kanade’s algorithm is used for stock analysis. It becomes a handy tool to determine the best time to sell or purchase the stocks to maximize profits.
- Budget Forecasting – Efficient predictions can be determined to increase efficiency and resource assignment.
- Data mining and analysis – Retrieving efficient trends and patterns in consecutive data such as time-series examination.
- Genomics – Kanade’s algorithm studies complex DNA structures and determines areas with noteworthy attributes.
- ML – In machine learning, it finds new patterns with optimized performance based on old data.
Complexity Analysis
Time complexity – Kanade’s algorithm has a 0(n) time complexity. It means the time for execution is directly proportional to the array size. As the size of the array increases/decreases, the execution time will increase/decrease accordingly.
Space complexity – The space required to store the Output is constant. Hence, the space complexity is 0(1).
Dynamic Programming
Dynamic programming is a method that divides a significant problem into several sub-problems. Each sub-problem is solved individually, and the Output is saved for future use.
Kanade’s algorithm is one of the examples of Dynamic programming. Here, as we iterate through the array, at every index of the array, the maximum sum at that index and the global sum are determined and saved at dq[z]. This saved Output is used at the next step or following index. In this way, the calculation reaches the last element or the last index of the array, and the most significant sum of the contiguous subarray is found.
1. Implementation using C++
Code:
#include <bits/stdc++.h>
using namespace std;
void maxSumContSubArrayBydynamic(int b[], int array_size)
{
vector dq(array_size, 0);
dq[0] = b[0];
int ans = dq[0];
for (int z = 1; z < array_size; z++) {
dq[z] = max(b[z], b[z] + dq[z - 1]);
ans = max(ans, dq[z]);
}
cout << "Using dynamic approach in C++, the largest sum contiguous
subarray is: " << ans;;
}
int main()
{
int b[] = {1,-2,3,-4,5,-6 };
int n = sizeof(b) / sizeof(b[0]);
maxSumContSubArrayBydynamic(b, n);
return 0;
}Output:
2. Implementation using Python
Code:
def maxSumContSubArrayBydynamic(array):
array_size = len(array)
dq = [0] * array_size
dq[0] = array[0]
ans = dq[0]
for z in range(1, array_size):
dq[z] = max(array[z], array[z] + dq[z - 1])
ans = max(ans, dq[z])
print("Using dynamic approach in python, the largest sum contiguous
subarray is:", ans)
if __name__ == "__main__":
a = [1,-2,3,-4,5,-6]
maxSumContSubArrayBydynamic(a)Output:
3. Implementation using JAVA
Code:
public class Main {
public static void maxSumContSubArrayBydynamic(int[] array) {
int array_size = array.length;
int[] dq = new int[array_size];
dq[0] = array[0];
int output = dq[0];
for (int z = 1; z < array_size; z++) {
dq[z] = Math.max(array[z], array[z] + dq[z - 1]);
output = Math.max(output, dq[z]);
}
System.out.println("Using dynamic approach in Java, the largest sum contiguous subarray is: " + output);
}
public static void main(String[] args) {
int[] a = { 1, -2, 3, -4, 5, -6};
maxSumContSubArrayBydynamic(a);
}
}Crucial Steps
- The dynamic programming approach focuses on storing intermediate values and, to do that, defining an array.
- Assign the 1st item of the input array to the 1st index of the new array.
- Take a new variable to store the 1st item of the new array.
- Now, using a For loop, iterate through the array and find the most significant values between the current element, the sum of the present component, and the previous maximum.
- Keep updating the variable accordingly.
Brute Force Approach
The brute force approach works on the principle of systematically working on every subarray possible within an array to find the sum of each subarray and store it through variables. The global sum is updated to the value of the current subarray if the value of the current subarray surpasses the value of the global sum. This process is carried out at every step where a subarray is found. At the end of the last subarray, we get the final global sum, our most considerable sum contiguous subarray.
1. Using a simple approach
The Simple approach usually focuses on using simple iteration methods.
- We will define a function that takes the parameter “array.” The array is the list of numbers of which the most significant sum contiguous subarray will be calculated. Then we define a few variables like n ( length of the array ), max_sum ( initially set of negative ), and indices of the subarray.
- Then, we iterate through the array using a nested for loop. The outer loop tracks the origin index of the possible subarray, and the inner loop is for the ending index.
- The current sum of the subarray and the global sum of the array are calculated. If the current sum is greater than the global sum, the global sum is updated with the value of the current sum, or else it remains unchanged.
- In the end, it returns the Output of our problem. In our case, the most significant sum contiguous subarray is 5.
1) Implementation using Python
Code:
def maxSumOfSubArrayByBrute(array):
n = len(array)
max_Sum = float('-inf')
origin = end = 0
for a in range(n):
for b in range(a, n):
currentSum = sum(array[a:b+1])
if currentSum > max_Sum:
max_Sum = currentSum
origin, end = a, b
return array[origin:end+1], max_Sum
array = [1, -2, 3, -4, 5, -6]
subarray, max_sum = maxSumOfSubArrayByBrute(array)
print("Using Brute Force Approach in Python, the Largest Sum Contiguous Subarray is", subarray)
print("Maximum sum:", max_sum)Output:
2) Implementation using C++
Code:
#include
#include
#include
using namespace std;
pair<int, pair<int, int>> maxSumOfSubArrayByBrute(vector& array) {
int n = array.size();
int max_Sum = INT_MIN;
int origin = 0, end = 0;
for (int a = 0; a < n; ++a) {
for (int b = a; b < n; ++b) {
int currentSum = 0;
for (int k = a; k <= b; ++k) { currentSum += array[k]; } if (currentSum > max_Sum) {
max_Sum = currentSum;
origin = a;
end = b;
}
}
}
return {max_Sum, {origin, end}};
}
int main() {
vector array = {1, -2, 3, -4, 5, -6};
auto result = maxSumOfSubArrayByBrute(array);
cout << "Using Brute Force Approach in C++, the Largest Sum Contiguous Subarray is: [";
for (int a = result.second.first; a <= result.second.second; ++a) {
cout << array[a] << " ";
}
cout << "]\n";
cout << "Maximum sum: " << result.first << endl;
return 0;
}Output:
3) Implementation using Java
Code:
public class Main {
public static void main(String[] args) {
int[] array = {1, -2, 3, -4, 5, -6};
int[] result = maxSumOfSubArrayByBrute(array);
System.out.println("Using Brute Force Approach in Java, the Largest Sum Contiguous Subarray is: " + java.util.Arrays.toString(result));
System.out.println("Maximum sum: " + result[result.length - 1]);
}
public static int[] maxSumOfSubArrayByBrute(int[] array) {
int n = array.length;
int max_Sum = Integer.MIN_VALUE;
int origin = 0, end = 0;
for (int a = 0; a < n; a++) {
for (int b = a; b < n; b++) { int currentSum = sumSubarray(array, a, b); if (currentSum > max_Sum) {
max_Sum = currentSum;
origin = a;
end = b;
}
}
}
int[] subarray = new int[end - origin + 1];
System.arraycopy(array, origin, subarray, 0, subarray.length);
subarray[subarray.length - 1] = max_Sum;
return subarray;
}
private static int sumSubarray(int[] array, int origin, int end) {
int sum = 0;
for (int k = origin; k <= end; k++) {
sum += array[k];
}
return sum;
}
}Output:
2. Using a Naive approach
Explanation – This approach means to code without many advanced methods and techniques. Here, we will be using three loops to iterate through arrays. As the first loop (a) starts, it remarks the origin index of the subarray. Similarly, the middle loop (b) represents the ending index of the subarray. The last loop or inner loop ( c ) performs the actual calculation of the derived subarray. In this way, the sum of each sub-array is calculated, and the global sum is updated if the current sum surpasses the value of global_sum
1) Implementation using Python
def maxSumContSubArrayByNaive(array):
global_sum = None
for a in range(len(array)):
start_idx = a
for b in range(a, len(array)):
sub_array_sum = sum(array[a:b + 1])
if global_sum is None or global_sum < sub_array_sum:
global_sum = sub_array_sum
return global_sum
array = [1, -2, 3, -4, 5, -6]
output = maxSumContSubArrayByNaive(array)
print("Using Naive approach in Python, the largest sum contiguous subarray is:",output)Output:
2) Implementation using Java
public class Main {
public static int maxSumContSubArrayByNaive(int[] array) {
int global_sum = Integer.MIN_VALUE;
for (int a = 0; a < array.length; a++) {
int startIdx = a;
for (int b = a; b < array.length; b++) {
int subarray_Sum = 0;
for (int c = a; c <= b; c++) {
subarray_Sum += array[c];
}
global_sum = Math.max(global_sum, subarray_Sum);
}
}
return global_sum;
}
public static void main(String[] args) {
int[] input_Array = {1, -2, 3, -4, 5, -6};
int output = maxSumContSubArrayByNaive(input_Array);
System.out.println(output);
}
}Output:
3 ) Implementation using C++
#include <iostream>
#include <climits>
int maxSumContSubArrayByNaive(int array[], int size) {
int globalSum = INT_MIN;
for (int a = 0; a < size; a++) {
for (int b = a; b < size; b++) {
int subarray_Sum = 0;
for (int c = a; c <= b; c++) {
subarray_Sum += array[c];
}
globalSum = std::max(globalSum, subarray_Sum);
}
}
return globalSum;
}
int main() {
int input_Array[] = {1, -2, 3, -4, 5, -6};
int array_size = sizeof(input_Array) / sizeof(input_Array[0]);
int output = maxSumContSubArrayByNaive(input_Array, array_size);
std::cout << "Using Naive approach in C++, the largest sum contiguous
subarray is: " << output << std::endl;
return 0;
}Output:
3. Using the Optimal approach
The best optimal approach is Kanade’s algorithm, which we have covered previously. But the Brute Force approach can also be optimized, and the best way to do it is to reduce the number of calculations and increase the efficiency of the code. To achieve this, we will be following the concept of running sum.
1) Implementation using Python
def maxSumOfSubArrayByBrute(array):
n = len(array)
max_Sum = float('-inf')
origin = end = 0
for a in range(n):
currentSum = 0
for b in range(a, n):
currentSum += array[b]
if currentSum > max_Sum:
max_Sum = currentSum
origin, end = a, b
return array[origin:end + 1], max_Sum
array = [1, -2, 3, -4, 5, -6]
subarray, max_sum = maxSumOfSubArrayByBrute(array)
print("Using Brute Force Approach with optimal approach in python, the Largest Sum Contiguous Subarray is:", subarray)
print("Maximum sum:", max_sum)Output:
2) Implementation using C++
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
pair<vector<int>, int> maxSumOfSubArrayByBrute(vector<int>& array) {
int n = array.size();
int max_Sum = INT_MIN;
int origin = 0, end = 0;
for (int a = 0; a < n; ++a) {
int currentSum = 0;
for (int b = a; b < n; ++b) {
currentSum += array[b];
if (currentSum > max_Sum) {
max_Sum = currentSum;
origin = a;
end = b;
}
}
}
vector<int> result(array.begin() + origin, array.begin() + end + 1);
return make_pair(result, max_Sum);
}
int main() {
vector<int> array = {1, -2, 3, -4, 5, -6};
pair<vector<int>, int> result = maxSumOfSubArrayByBrute(array);
cout << "Using Brute Force Approach with optimal approach in C++, the
Largest Sum Contiguous Subarray is: [";
for (int num : result.first) {
cout << num << " ";
}
cout << "]\n";
cout << "Maximum sum: " << result.second << endl;
return 0;
}Output:
3) Implementation using Java
public class Main {
public static int[] maxSumOfSubArrayByBrute(int[] array) {
int n = array.length;
int max_Sum = Integer.MIN_VALUE;
int origin = 0, end = 0;
for (int a = 0; a < n; ++a) {
int currentSum = 0;
for (int b = a; b < n; ++b) {
currentSum += array[b];
if (currentSum > max_Sum) {
max_Sum = currentSum;
origin = a;
end = b;
}
}
}
return java.util.Arrays.copyOfRange(array, origin, end + 1);
}
public static void main(String[] args) {
int[] array = {1, -2, 3, -4, 5, -6};
int[] result = maxSumOfSubArrayByBrute(array);
System.out.print("Using Brute Force Approach with optimal approach in
JAVA, the Largest Sum Contiguous Subarray is: [");
for (int num : result) {
System.out.print(num + " ");
}
System.out.println("]");
System.out.println("Maximum sum: " +
java.util.Arrays.stream(result).sum());
}
}Output:
Divide and Conquer Approach
The Divide and Conquer approach divides the main array into several sub-arrays. The solution for each sub-array is determined iteratively, and then the results are combined to find the final Output.
1) Implementation using Python
def maxSumOfSubArrayByDivConq(array, low_point, mid_point, high_point):
left_sum = float('-inf')
sum = 0
for a in range(mid_point, low_point - 1, -1):
sum += array[a]
if sum > left_sum:
left_sum = sum
right_sum = float('-inf')
sum = 0
for a in range(mid_point + 1, high_point + 1):
sum += array[a]
if sum > right_sum:
right_sum = sum
return left_sum + right_sum
def max_subarray_sum(array, low_point, high_point):
if low_point == high_point:
return array[low_point]
mid_point = (low_point + high_point) // 2
left_sum = max_subarray_sum(array, low_point, mid_point)
right_sum = max_subarray_sum(array, mid_point + 1, high_point)
cross_sum = maxSumOfSubArrayByDivConq(array, low_point, mid_point,
high_point)
return max(left_sum, right_sum, cross_sum)
# Example usage:
array = [1,-2,3,-4,5,-6]
output = max_subarray_sum(array, 0, len(array) - 1)
print("Using Divide and Conquer approach in Python, Largest Sum Contiguous
Subarray:", output)output:
2) Implementation using C++
#include <iostream>
#include <climits>
#include <vector>
using namespace std;
int maxSumOfSubArrayByDivConq(const vector<int>& array, int low_point, int
mid_point, int high_point) {
int left_sum = INT_MIN;
int sum = 0;
for (int a = mid_point; a >= low_point; --a) {
sum += array[a];
if (sum > left_sum) {
left_sum = sum;
}
}
int right_sum = INT_MIN;
sum = 0;
for (int a = mid_point + 1; a <= high_point; ++a) {
sum += array[a];
if (sum > right_sum) {
right_sum = sum;
}
}
return left_sum + right_sum;
}
int max_subarray_sum(const vector<int>& array, int low_point, int high_point)
{
if (low_point == high_point) {
return array[low_point];
}
int mid_point = (low_point + high_point) / 2;
int left_sum = max_subarray_sum(array, low_point, mid_point);
int right_sum = max_subarray_sum(array, mid_point + 1, high_point);
int cross_sum = maxSumOfSubArrayByDivConq(array, low_point, mid_point,
high_point);
return max(left_sum, max(right_sum, cross_sum));
}
int main() {
vector<int> array = {1,-2,3,-4,5,-6};
int result = max_subarray_sum(array, 0, array.size() - 1);
cout << "Using Divide and Conquer approach in C++, Largest Sum Contiguous
Subarray: " << result << endl;
return 0;
}output:
3) Implementation using Java
import java.util.Arrays;
public class Main {
private static int maxSumOfSubArrayByDivConq(int[] array, int low_point,
int mid_point, int high_point) {
int leftSum = Integer.MIN_VALUE;
int sum = 0;
for (int a = mid_point; a >= low_point; a--) {
sum += array[a];
if (sum > leftSum) {
leftSum = sum;
}
}
int rightSum = Integer.MIN_VALUE;
sum = 0;
for (int a = mid_point + 1; a <= high_point; a++) {
sum += array[a];
if (sum > rightSum) {
rightSum = sum;
}
}
return leftSum + rightSum;
}
private static int maxSubarraySum(int[] array, int low_point, int
high_point) {
if (low_point == high_point) {
return array[low_point];
}
int mid_point = (low_point + high_point) / 2;
int leftSum = maxSubarraySum(array, low_point, mid_point);
int rightSum = maxSubarraySum(array, mid_point + 1, high_point);
int crossSum = maxSumOfSubArrayByDivConq(array, low_point, mid_point,
high_point);
return Math.max(Math.max(leftSum, rightSum), crossSum);
}
public static void main(String[] args) {
int[] array = {1,-2,3,-4,5,-6};
int result = maxSubarraySum(array, 0, array.length - 1);
System.out.println("Using Divide and Conquer approach in Java, Largest
Sum Contiguous Subarray: " + result);
}
}output:
Comparison of Time and Space Complexities
| Approach | Time Complexity | Space Complexity |
| Brute Force Approach | O(n^2) | O(1) |
| Simple Approach | O(n) | O(1) |
| Naïve Approach | O(n^2) | O(1) |
| Optimal Approach | O(n) | O(1) |
| Divide and Conquer Approach | O(n log n) | O(log n) |
Conclusion
We learned about different approaches and their complexity for finding the largest Sum Contiguous Subarray, where Kadane’s algorithm, brute force approaches, and Dynamic programming play crucial roles. It has real-world applications in stock market analysis, machine learning, and signal and image processing. Optimal solutions are considered by understanding their method, time, and space complexity.
FAQs
Q1. How does Kadane’s algorithm handle an array with all negative elements?
Answer: To handle an all-negative array, Kadane’s algorithm follows three different approaches:
Approach1: Standard Kadane’s algorithm:
For an Array with all harmful elements, it returns 0 as the maximum sum because adding a negative value will only decrease the sum
Approach2: Finding the minimum element:
Instead of maximizing, it minimizes the sum by the comparison operator as it returns the most minor negative element in an array as the maximum sum.
Approach3: Initializing with minimum value:
Initialized with a significant negative value for max_ending_here variable, so that adding negative value will be less than maximum_ending _here; hence, it will identify the least negative element as the maximum sum
Q2. How can we apply the divide and conquer approach for non-numeric datasets
Answer: The Divide and conquer approach is applied to the numerical array to find the maximum sum through comparison. However, it can be used for non-numeric datasets with some adaptations through the following steps:
Step 1: Convert the non-numeric element into a numeric element while maintaining the order of an array. We can use ASCII code to assign its numeric value for string-based arrays.
Step 2: Adjust the comparison logic of the divide and conquer algorithm with the nature of the numeric array and use relevant logic for the converted numeric datasets
Step 3: Implement the algorithm with the converted numeric representation of the array and comparison logic.
Q3. Can we parallelize the algorithms for distributed computing?
Answer: We can parallelize Kadane’s algorithm and divide-and-conquer approaches for distributed computing. The method splits the datasets into small segments and processes them on different computing nodes. The resultant local maximum subarray sum is combined with the global entire subarray sum by merging the results from other nodes.
Recommended Articles
We hope this EDUCBA information on “Largest Sum Contiguous Subarray” benefited you. You can view EDUCBA’s recommended articles for more information.