Updated April 15, 2023

Introduction to AVL Tree Python
In Python, AVL Adelson-Velskii and Landis (AVL) trees are defined as a unit binary tree that area unit balanced. The AVL tree could be a self-balancing binary search tree within which every node keeps track of extra info termed a balance issue, which may be -1, 0, or 1. The distinction between the heights of a node’s left Associate in Nursing right subtrees is that the balance issue of that node in an AVL tree. (Height of Left Subtree – Height of Right Subtree) or (Height of Left Subtree – Height of Right Subtree) (Height of Right Subtree – Height of Left Subtree).
Syntax or Algorithm
As this is a data structure concept we do not have a particular syntax but follow some rules or steps that will be given as an algorithm for finding or inserting or deleting any element in this AVL tree. Therefore let us see the steps for inserting and deleting the elements in the AVL tree are as below:
Insertion:
- Step 1: initial, use BST’s (Binary Search Tree) insertion logic to feature a replacement member to the tree.
- Step 2: once you’ve got inserted all of the components, you will need to visualize every node’s Balance issue.
- Step 3: once the Balance issue of every node is discovered to be zero or one or -1, the algorithmic program moves on to a successive step.
- Step 4: If any node’s balance issue isn’t one in every one of the 3 values listed higher than, the tree is taken into account to be unbalanced. The algorithmic program can then proceed to successive operation once performing arts the suitable Rotation to form it balanced.
Deletion:
- Step 1: find the node wherever k is held on.
- Step 2: at the moment, erase the node’s contents (Suppose the node is x)
- Step 3: create a claim: Delete a leaf to lower the scale of a node in the Associate in Nursing AVL tree. There are a unit 3 eventualities that might occur:
- Delete x once it’s no youngsters.
- Let x’ become child the child} of x once x has one kid.
- Because T subtrees will solely take issue tall by one, x’ cannot have a child:
- then take away x’ and replace the contents of x with the contents of x’ (a leaf)
- Step 4: If x has 2 youngsters, find x’s successor, z (who doesn’t have a left child), replace x’s contents with z’s contents, and take away z.
How to Implement the AVL Tree in Python?
In Python, the AVL tree is known as a self-balancing tree which uses a balance factor whose value is -1, 0, or +1 and it has 4 different operations and it can be elaborated as below:
Operations on AVL tree along with separate trees can be as follows:
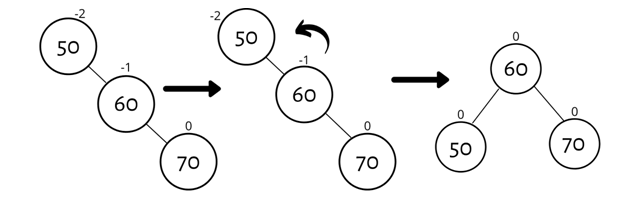
1. Rotation to the Left (LL)
Node y becomes the new subtree’s root once we rotate left around node x. Node x becomes the left kid of node y, and subtree b becomes the proper kid of node x.
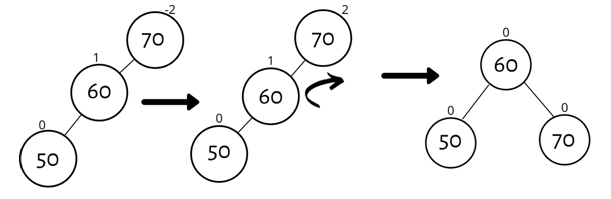
2. Right Rotation (RR)
Node x becomes the new root of the subtree once we right rotate concerning node y. Subtree b becomes the left kid of node y, whereas node y becomes the proper kid of subtree b.
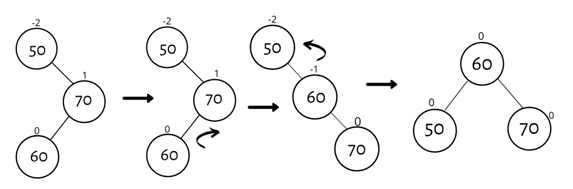
3. Left Right Rotation (LR Rotation)
This sort of rotation involves a left rotation and a right rotation because the name implies.
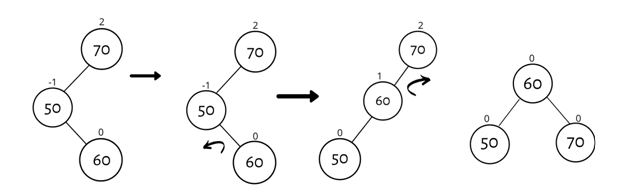
4. Right Left Rotation (RL Rotation)
This sort of rotation consists of a rotation to the proper and a rotation to the left.
Examples of AVL Tree Python
In the below example we are writing Python code for showing both insertion and deletion in AVL tree.
Code:
import sys
class treeroot(object):
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class avl(object):
def insrtnode(self, root, key):
if not root:
return treeroot(key)
elif key < root.key: root.left = self.insrtnode(root.left, key) else: root.right = self.insrtnode(root.right, key) root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) balanceFactor = self.getBalance(root) if balanceFactor > 1:
if key < root.left.key:
return self.RR(root)
else:
root.left = self.LR(root.left)
return self.RR(root)
if balanceFactor < -1: if key > root.right.key:
return self.LR(root)
else:
root.right = self.RR(root.right)
return self.LR(root)
return root
def delnode(self, root, key):
if not root:
return root
elif key < root.key: root.left = self.delnode(root.left, key) elif key > root.key:
root.right = self.delnode(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = self.getMinValueNode(root.right)
root.key = temp.key
root.right = self.delnode(root.right,
temp.key)
if root is None:
return root
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
bf = self.getBalance(root)
if bf > 1:
if self.getBalance(root.left) >= 0:
return self.RR(root)
else:
root.left = self.LR(root.left)
return self.RR(root)
if bf < -1:
if self.getBalance(root.right) <= 0:
return self.LR(root)
else:
root.right = self.RR(root.right)
return self.LR(root)
return root
def LR(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def RR(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def getHeight(self, root):
if not root:
return 0
return root.height
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def getMinValueNode(self, root):
if root is None or root.left is None:
return root
return self.getMinValueNode(root.left)
def preOrder(self, root):
if not root:
return
print("{0} ".format(root.key), end="")
self.preOrder(root.left)
self.preOrder(root.right)
def printHelper(self, currPtr, indent, last):
if currPtr != None:
sys.stdout.write(indent)
if last:
sys.stdout.write("R----")
indent += " "
else:
sys.stdout.write("L----")
indent += "| "
print(currPtr.key)
self.printHelper(currPtr.left, indent, False)
self.printHelper(currPtr.right, indent, True)
myTree = avl()
root = None
nums = [95, 45, 27, 19, 71, 10, 68, 34]
for num in nums:
root = myTree.insrtnode(root, num)
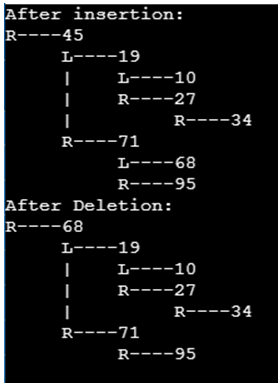
print("After insertion: ")
myTree.printHelper(root, "", True)
key = 45
root = myTree.delnode(root, key)
print("After Deletion: ")
myTree.printHelper(root, "", True)Output:
In the above example, we can see we have written code on inserting and deleting the elements in the AVL tree where first we import sys file to implement this in Python. Later we have defined classes treeroot and AVL where in treeroot we are just using it to define key, left, right, and even height factors so that we can use it in further balance factor and other rotation operation. In class AVL we are defining how to insert and delete with separate functions which are called in the main function. The output is as shown in the above screenshot.
Conclusion
In this article, we conclude that where this AVL is associated binary search tree for nursing automobile equilibrating where no large difference between right and left subtrees and hence rearranging them would make it display as self-balancing which will further redeploy these allocations with sure rotations.
Recommended Articles
This is a guide to AVL Tree Python. Here we also discuss the introduction, syntax, and how to implement AVL Tree in Python along with different examples and its code implementation. You may also have a look at the following articles to learn more –