Updated April 4, 2023

Introduction to Binary search tree C++
Binary search tree in C++ is defined as a data structure that consists of the node-based binary tree where each node consists of at most 2 nodes that are referred to as child nodes. This tree is also known as an ordered or sorted tree. Using this concept, one can store numbers in an organized way and binary tree helps in a quick search, add, and/or delete operations to be performed on the dataset. Using the concept one can implement dynamic sets and lookup tables. The structure of the binary tree enables skipping of half of the remaining tree thus leading to better time complexity with the average being O(log n) for search, add, and/or delete operations. This methodology is better than the linear search due to its improved time complexity. In this article, we will look at all the concepts of add, search and delete in great detail.
Syntax
Retrieve the value of root in a Binary Search tree:
root->keyPoint to the left of the root in a Binary Search tree:
root->leftPoint to the right of the root in a Binary Search tree:
root->rightHow does Binary search tree works in C++?
By now we understand that the Binary Search tree (BST) has a root node and at max 2 child node either on to left or right or both. The algorithm in a BST undergoes operations by comparison of values in the root node, and subsequently it being lesser or more, the navigation in the tree takes place accordingly. In the working of Binary search tree, 3 operations are performed, namely:
- Insert: In this operation if the tree is empty, the first value that is inserted is always the root node, now when the next value is inserted, it compares if the value is greater than the root node or not. If greater it gets inserted to the right-hand side and if not, it moves to the left. If there is already a left side existing while inserting, it checks till the last node is hit and subsequently based on it being more or less, gets inserted into the corresponding location of the node.
- Search: This is fairly an easy operation, where the number which needs to be search is compared against the node values that are present. If the value that needs to be searched is more than the node value, the right side of the tree is searched and vice versa. In this way, we can avoid the other half of the tree which need not be searched as the binary tree is an ordered one. Till the end, if the node is NULL, we return that the value is not found.
- Delete: Finally coming to the delete, which is one of the toughest amongst the three, but here we are to simplify it for you. When we delete, we might have 3 possibilities that we will discuss below one by one:
Case 1: The leaf node is to be deleted. When the number which needs to be deleted lies in the leaf, which means that there are no other values as a branch, we simply navigate to that location and delete the leaf node.
Case 2: One leaf node is attached to the root node. Here we navigate to the node which contains one leaf node, delete the node and assign that leaf node as the root node.
Case 3: The node that needs to be deleted has 2 leaf nodes connected to it. Here we find the in-order successor of the node, then copy all the contents of the in order successor followed by replacing the deleted node with the in order successor and pasting the contents of the in order successor at the node which replaced the deleted node. In-order successor is the maximum value on the right side of the tree from the node where the value is deleted from.
With the understanding of the above 3 process, it will be easier to now look at some examples, to get the practical experience of the theory we just learnt.
Examples
Here are the following examples mentioned below:
Example #1
Insert in Binary Search Tree in C++
Syntax
#include <iostream>
using namespace std;
class nodeBST
{
int key;
nodeBST *lft, *rgt;
public:
nodeBST();
nodeBST(int);
nodeBST* insertFunc(nodeBST*, int);
void traverseInOrder(nodeBST*);
};
nodeBST ::nodeBST()
: key(0)
, lft(NULL)
, rgt(NULL)
{
}
nodeBST ::nodeBST(int value)
{
key = value;
lft = rgt = NULL;
}
nodeBST* nodeBST ::insertFunc(nodeBST* root, int value)
{
if (!root)
{
return new nodeBST(value);
}
if (value > root->key)
{
root->rgt = insertFunc(root->rgt, value);
}
else
{
root->lft = insertFunc(root->lft, value);
}
return root;
}
void nodeBST ::traverseInOrder(nodeBST* root)
{
if (!root) {
return;
}
traverseInOrder(root->lft);
cout << root->key << endl;
traverseInOrder(root->rgt);
}
int main()
{
nodeBST node, *root = NULL;
root = node.insertFunc(root, 0);
node.insertFunc(root, 27);
node.insertFunc(root, 9);
node.insertFunc(root, 19);
node.insertFunc(root, 91);
node.insertFunc(root, 2);
node.insertFunc(root, 7);
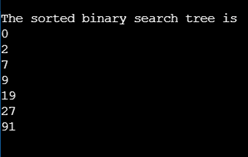
cout<<"\nThe sorted binary search tree is "<< endl;
node.traverseInOrder(root);
return 0;
}Output:
Example #2
Search in Binary Search Tree in C++.
Syntax
#include <iostream>
using namespace std;
class nodeBST
{
public:
int key;
nodeBST *lft, *rgt;
nodeBST();
nodeBST(int);
nodeBST* insertFunc(nodeBST*, int);
nodeBST* searchFunc(nodeBST*, int);
void traverseInOrder(nodeBST*);
};
nodeBST ::nodeBST()
: key(0)
, lft(NULL)
, rgt(NULL)
{
}
nodeBST ::nodeBST(int value)
{
key = value;
lft = rgt = NULL;
}
nodeBST* nodeBST ::insertFunc(nodeBST* root, int value)
{
if (!root)
{
return new nodeBST(value);
}
if (value > root->key)
{
root->rgt = insertFunc(root->rgt, value);
}
else
{
root->lft = insertFunc(root->lft, value);
}
return root;
}
nodeBST* nodeBST ::searchFunc(nodeBST* root, int key)
{
if (root == NULL || root->key == key)
return root;
if (root->key < key)
return searchFunc(root->rgt, key);
return searchFunc(root->lft, key);
}
void nodeBST ::traverseInOrder(nodeBST* root)
{
if (!root) {
return;
}
traverseInOrder(root->lft);
cout << root->key << endl;
traverseInOrder(root->rgt);
}
int main()
{
nodeBST node, *root = NULL, *searchRoot = NULL;
root = node.insertFunc(root, 0);
node.insertFunc(root, 27);
node.insertFunc(root, 9);
node.insertFunc(root, 19);
node.insertFunc(root, 91);
node.insertFunc(root, 2);
node.insertFunc(root, 7);
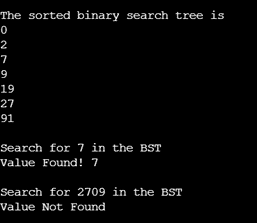
cout<<"\nThe sorted binary search tree is "<< endl;
node.traverseInOrder(root);
cout<<"\nSearch for 7 in the BST "<< endl;
searchRoot = node.searchFunc(root, 7);
if(searchRoot == NULL)
{
cout<<"Value Not Found\n";
}
else
{
cout << "Value Found! "<<searchRoot->key<<"\n";
}
cout<<"\nSearch for 2709 in the BST "<< endl;
*searchRoot = NULL;
searchRoot = node.searchFunc(root, 2709);
if(searchRoot == NULL)
{
cout<<"Value Not Found\n";
}
else
{
cout << "Value Found! "<<searchRoot->key<<"\n";
}
return 0;
}Output:
Example #3
Delete in Binary Search Tree in C++.
Syntax
#include <bits/stdc++.h>
using namespace std;
struct node {
int key;
struct node *lft, *rgt;
};
struct node* newNode(int item)
{
struct node* temp
= (struct node*)malloc(sizeof(struct node));
temp->key = item;
temp->lft = temp->rgt = NULL;
return temp;
}
void inorder(struct node* root)
{
if (root != NULL) {
inorder(root->lft);
cout << root->key << " ";
inorder(root->rgt);
}
}
struct node* insertFunc(struct node* node, int val)
{
if (!node)
{
return newNode(val);
}
if (val > node->key)
{
node->rgt = insertFunc(node->rgt, val);
}
else
{
node->lft = insertFunc(node->lft, val);
}
return node;
}
struct node* minValueNode(struct node* node)
{
struct node* current = node;
while (current && current->lft != NULL)
current = current->lft;
return current;
}
struct node* deleteFunc(struct node* root, int key)
{
if (root == NULL)
return root;
if (key < root->key)
root->lft = deleteFunc(root->lft, key);
else if (key > root->key)
root->rgt = deleteFunc(root->rgt, key);
else {
if (root->lft==NULL and root->rgt==NULL)
return NULL;
else if (root->lft == NULL) {
struct node* temp = root->rgt;
free(root);
return temp;
}
else if (root->rgt == NULL) {
struct node* temp = root->lft;
free(root);
return temp;
}
struct node* temp = minValueNode(root->rgt);
root->key = temp->key;
root->rgt = deleteFunc(root->rgt, temp->key);
}
return root;
}
int main()
{
struct node* root = NULL;
root = insertFunc(root, 27);
root = insertFunc(root, 9);
root = insertFunc(root, 19);
root = insertFunc(root, 91);
root = insertFunc(root, 2);
root = insertFunc(root, 7);
root = insertFunc(root, 0);
root = insertFunc(root, 1);
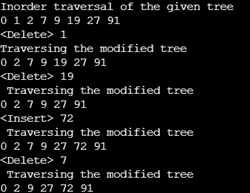
cout << "Inorder traversal of the given tree \n";
inorder(root);
cout << "\n<Delete> 1\n";
root = deleteFunc(root, 1);
cout << "Traversing the modified tree \n";
inorder(root);
cout << "\n<Delete> 19\n";
root = deleteFunc(root, 19);
cout << " Traversing the modified tree \n";
inorder(root);
cout << "\n<Insert> 72\n";
root = insertFunc(root, 72);
cout << " Traversing the modified tree \n";
inorder(root);
cout << "\n<Delete> 7\n";
root = deleteFunc(root, 7);
cout << " Traversing the modified tree \n";
inorder(root);
return 0;
}Output:
Conclusion
In this article, we have looked into the operations that are possible using the binary search tree, and the corresponding methodology in theory along with the practical aspect of it through 3 examples that covers the entire learning space of the binary search tree.
Recommended Articles
This is a guide to Binary search tree C++. Here we discuss the operations that are possible using the binary search tree, and the corresponding methodology in theory. You may also have a look at the following articles to learn more –