Updated April 6, 2023

Definition of Binary Search Tree
A binary search tree is a data structure that allows us to keep a sorted list of numbers in a short amount of time. It is also called a binary tree because each tree node can only have two siblings. The binary search tree may be used to search for the presence of a number; it is termed a search tree. The running time complexity is O(log(n)) time; the characteristics that distinguish a binary search tree from a basic binary tree are as follows –
1. The nodes of the left subtree are all smaller than the root node.
2. The nodes of the right subtree are all greater than the root node.
3. Each node of the subtrees is likewise BSTs, meaning they have the same two qualities as the node itself.
Working on the binary search tree in Java
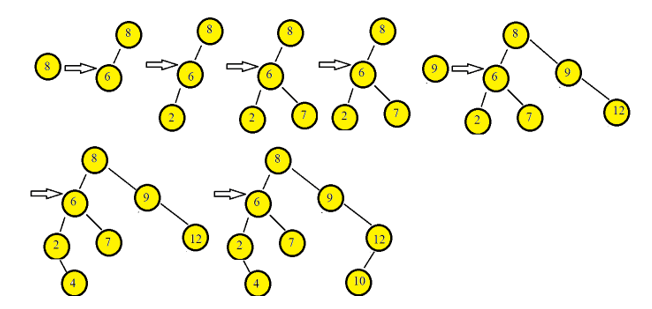
1. Let the specified array is:
Given array: [8, 6, 2, 7, 9, 12, 4, 10]
2. Let’s start with the top element 43. Insert 43 as the tree’s root.
3. If the next element is less than the root node element, it should be inserted as the root of the left sub-tree.
4. If not, it should be inserted as the root of the right sub-tree.
The image below depicts the process of constructing a binary search tree using the provided elements.
Binary search tree operations:
The operations supported by the binary search tree in Java are shown in the below list –
1. Searching in BST – In a binary search tree, finding the position of a certain element.
2. Insertion in BST – Adding a new element to the binary search tree in the proper location ensures that the binary search tree property is not broken.
3. Deletion in BST – Remove a specific node in a binary search tree. However, depending on the number of children a node has, there can be a variety of deletion scenarios.
Examples
Example for binary search tree in Java to perform an operation on the binary search tree –
Example #1
// The program can be tested in Eclipse IDE, JAVA 11
package jex;
import java.util.Scanner;
class binarySearchTree {
//node class that defines BST node
class Node {
int key;
Node left, right;
public Node(int data){
key = data;
left = right = null;
}
}
// binary search tree root node
Node root;
// Constructor for binary search tree, first empty tree
binarySearchTree(){
root = null;
}
//delete a node from binary search tree
void deleteKey(int key) {
root = delete(root, key);
}
//recursive delete function
Node delete(Node root, int key) {
// if tree is empty
if (root == null) return root;
//traverse the tree
if (key < root.key)
//traverse left subtree
root.left = delete(root.left, key);
else if (key > root.key)
//traverse right subtree
root.right = delete(root.right, key);
else {
// if node having only one child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// if node has two children;
root.key = minKey(root.right);
// removing the inorder sibling
root.right = delete(root.right, root.key);
}
return root;
}
int minKey(Node root) {
// initially min is root
int min = root.key;
// find minimum value
while (root.left != null) {
min = root.left.key;
root = root.left;
}
return min;
}
// insert a node in binary search tree
void insertKey(int key) {
root = insert(root, key);
}
// recursively insert a node
Node insert(Node root, int key) {
// initially, tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// traverse the tree
if (key<root.key)
//insert in the left subtree
root.left = insert(root.left, key);
else if (key > root.key)
//insert in the right subtree
root.right = insert(root.right, key);
// return
return root;
}
// function to travel inorder of binary search tree
void inorder() {
inorder(root);
}
// recursively traverse the binary search tree
void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
boolean searchKey(int key) {
root = search(root, key);
if (root!= null)
return true;
else
return false;
}
//recursive insert function
Node search(Node root, int key) {
// If root is null or key is present at root
if (root==null || root.key==key)
return root;
// when val is greater than root's key
if (root.key > key)
return search(root.left, key);
// when val is lesser than root's key
return search(root.right, key);
}
}
public class client{
public static void main(String[] args) {
binarySearchTree t = new binarySearchTree();
// inserting 8, 6, 2, 7, 9, 12, 4, 10 data into the binary search tree
t.insertKey(8);
t.insertKey(6);
t.insertKey(2);
t.insertKey(7);
t.insertKey(9);
t.insertKey(12);
t.insertKey(4);
t.insertKey(10);
//print the binary search tree
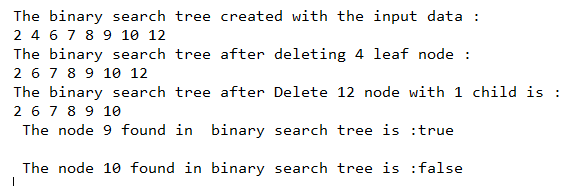
System.out.println( "The binary search tree created with the input data :");
t.inorder();
//delete the leaf node
System.out.println( "\nThe binary search tree after deleting 4 leaf node :");
t.deleteKey(4);
t.inorder();
//delete the node with one child
System.out.println( "\nThe binary search tree after Delete 12 node with 1 child is :");
t.deleteKey(12);
t.inorder();
//search a key in the binary search tree
boolean res = t.searchKey (9);
System.out.println( "\n The node 9 found in binary search tree is :" + res );
res = t.searchKey (12);
System.out.println( "\n The node 10 found in binary search tree is :" + res );
}
}Output:
As in the above program, the binarySearchTree class is created, which contains another inner class Node and also contains the constructor and methods. The methods defined in the class are deleteKey(), delete(), minKey(), insertKey(), insert(), inorder(), searchKey(), and search() to perform the specific operations. In the main function, the binarySearchTree class object is created, insert some elements into it, and next call the methods of the binary Search Tree class on its object, as seen in the above output.
Conclusion
The binary search tree is also known as a binary tree because each tree node can only have two siblings. A binary search tree is a data structure that allows keeping a sorted list of numbers in a short amount of time. The operation that can be performed on the binary search tree: traversing, inserting, deleting, and searching.
Recommended Articles
This is a guide to Binary Search Tree in Java. Here we discuss the Definition, working of the binary search tree in Java, and examples with code implementation. You may also have a look at the following articles to learn more –