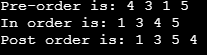Updated March 6, 2023

Definition of Binary Tree in Data Structure
Data structure provides the different types of trees to the user, and we can utilize them as per the user’s requirement. The binary tree is one tree type in the data structure; it is a special type of tree. In a binary tree, every node or every vertex has two child nodes or single child nodes, or no child node. Basically, a binary tree is a very important class in a data structure in which nodes of a binary tree have at most two children nodes. In the binary tree, the left side is called the left child node, and the right side of the binary tree is called the right child node.
Syntax:
struct b_node
{
int item;
struct b_node *left_node;
struct b_node *right_node;
};
Explanation:
In the above syntax, we represent a binary tree, here we use structure to represent the binary tree that contains two pointers with two items, one for the left child node and one for the right child node as shown in the above syntax.
How Binary Tree works in Data Structure?
Now let’s see how a binary tree works in a data structure as follows.
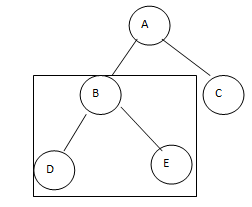
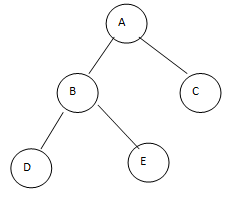
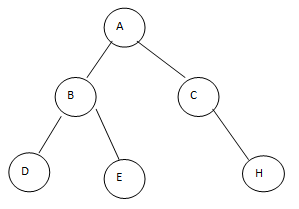
In above show the binary tree; see here above tree contains at most two child nodes, as shown in the above figure. Some important terms are used in binary trees as follows.
Path: Path is used to represent the sequence of nodes on either the left side or right side.
Root: The topmost node of the tree we call a root node, and each tree has only one root node; for example, A is a root node.
Parent: We can consider any node as a parent node except the root node, for example, B as a parent node.
Child: Below parent node tree contains the child node; for example, D and E is a child node of B.
Leaf: In a binary tree, the node does not have any child node that node we called a leaf node, for example, D.
Subtree: binary we contain the subtree for example, in the above binary, we show the subtree by using the square.
Keys: It is used to represent the value of a node, and that is used to perform the search and insert operation.
Now let’s see the basic operation of the Binary tree as follows.
Insert Operation:
Binary tree representation starts with the insertion operation. After that, we insert the node in its proper location, and the node location is based on the key value of the node.
Search Operation:
When we need to search for an element in the binary tree, then we start the searching from the root node and then compare the item value or element value with key values. If the search value is less than the key value, then we perform the search on the left side, and if the search value is greater than the key value, then we perform a search on the right side.
Preorder Traversal:
We traverse the node in a pre-order manner as per requirement.
Inorder Traversal:
We traverse the node in an in-order manner as per requirement.
Postorder Traversal:
We traverse the node in a post-order manner as per requirement.
Illustration of Binary Tree
Methods of binary trees are as follows.
1. Full or Strict or Proper Binary Tree
The full binary means if each node should have been 0 or 2 child nodes, then we say that this tree is a full binary tree, and full binary, we can also call it a strict binary tree. The simple example of a full binary tree we illustrated by using the following figure as follows.
2. Complete Binary Tree
The complete binary tree is a tree where every one of the nodes is totally filled with the exception of the last level. In the last level, every one of the nodes should be just about as left as could be expected. In a complete binary tree, the nodes should be added from the left side. The complete binary tree is illustrated by using the following figure as follows.
3. Perfect Binary Tree
In a perfect binary tree, if all internal nodes have 2 children nodes and all leaf nodes have the same level, then we can say this tree is a perfect binary tree. The perfect binary we illustrated by using the following figure as follows.
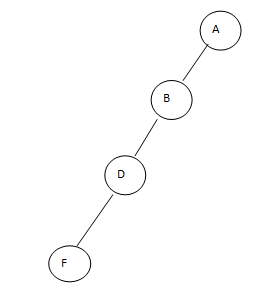
4. Degenerate Binary Tree
The degenerate binary tree means all internal nodes have only one child node, either the left side or the right side of the tree. The degenerate binary tree we illustrate by using the following figure as follows.
The above tree has only one child node, and it is also called a right-skewed tree. Similarly, we can draw the left-skewed tree.
5. Balanced Binary Tree
The balanced tree means both sides of the tree, that is left, and right sides of the tree, differ by at most 1. The balanced binary we illustrated by using the following figure as follows.
Example
Now let’s see the example of a binary tree in a data structure as follows.
class B_Node:
def __init__(self, key_value):
self.left_B = None
self.right_B = None
self.val_B = key_value
def PreOrder_B(self):
print(self.val_B, end=' ')
if self.left_B:
self.left_B.PreOrder_B()
if self.right_B:
self.right_B.PreOrder_B()
def InOrder_B(self):
if self.left_B:
self.left_B.InOrder_B()
print(self.val_B, end=' ')
if self.right_B:
self.right_B.InOrder_B()
def PostOrder_B(self):
if self.left_B:
self.left_B.PostOrder_B()
if self.right_B:
self.right_B.PostOrder_B()
print(self.val_B, end=' ')
root = B_Node(4)
root.left_B = B_Node(3)
root.right_B = B_Node(5)
root.left_B.left_B = B_Node(1)
print("Pre-order is: ", end="")
root.PreOrder_B()
print("\nIn order is: ", end="")
root.InOrder_B()
print("\nPost order is: ", end="")
root.PostOrder_B()
Explanation:
In the above example, we use python programming language to implement the binary tree in the data structure. In this example, we implement three different operations a pre-order tree traversal, in-order tree traversal, and postorder tree traversal, as shown in the above program. The final output of the above statement we illustrate by using the following snapshot.
Conclusion
We hope from this article, you have learned the Binary tree in a data structure. We have learned the basic syntax of the Binary tree, and we also see different examples of the Binary tree. We also learned how and when we use the Binary tree in a data structure.
Recommended Articles
This is a guide to Binary Tree in Data Structure. Here we discuss the definition, syntax, How Binary tree works in data structure?, Different types of binary tree, and examples with code implementation. You may also have a look at the following articles to learn more –