Updated March 13, 2023
Introduction to Binary Tree Types
The following article provides an outline for Binary Tree Types. A binary tree is a data structure in which each Node has a maximum of two children or each node connected to at most two subtrees. Those subtrees are also a binary tree. In a binary tree, there are three components.
- Value: Value store at Node
- *Left: Address of Left Child Node
- *Right: Address of Left-Right Node
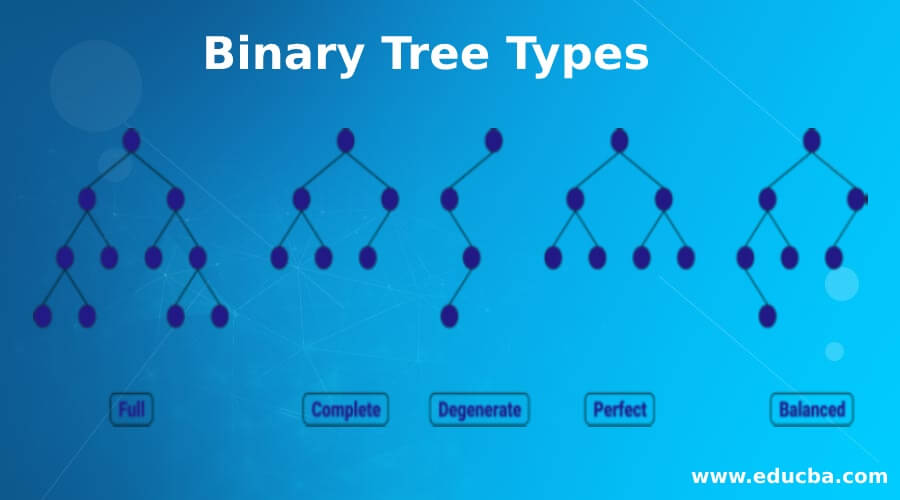
A Binary tree has many characteristics, and based on their characteristics there are 5 types of Binary Tree. Let’s understand in detail: –
Types of Binary Tree
Below are the different types of binary tree:
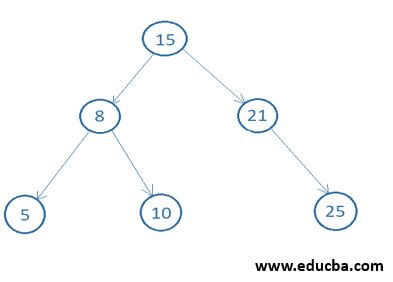
1. Full Binary Tree
A Full Binary Tree is a Binary Tree with an additional property that each node in the binary tree should have two children or no children. The node of which address stored in root node those nodes are called children node of root. Those nodes which have no children are called leaf nodes.
Let’s see whether a binary tree is a Full Binary Tree is or not. In the below code, we are taking binary tree as same as above. To check the full binary tree, we have to travel all the nodes; if any node has one child, then we simply return False. On the other hand, if all node has only two children or no children, then the only binary tree is called a full binary tree.
Code:
struct BTNode
{
int value; // element value
struct BTNode * left; //To store address of left child
struct BTNode * right; //To store address of right child
};
struct BTNode *GenerateBTNode(int data) {
struct BTNode *node = new BTNode;
node->value = data;
node->right = NULL;
node->left = NULL;
return node;
}
bool isFullTree(struct BTNode *root) {
if(root==NULL){
return true;
}
if (root->left==NULL && root->right==NULL) {
return true;
}
if(root->left!=NULL && root->right!=NULL) {
return(isFullTree(root->left) && (isFullTree(root->right)));
}
return false;
}
void displayTreeInorder (struct BTNode *root) {
if(root != NULL){
displayTreeInorder(root->left);
cout<<root->value<<endl;
displayTreeInorder(root->right);
}
}
int main(){
BTNode *root=NULL;
root = GenerateBTNode(10);
root->left = GenerateBTNode(8);
root->right = GenerateBTNode(15);
root->left->left = GenerateBTNode(12);
root->left->right = GenerateBTNode(13);
root->left->right->left = GenerateBTNode(18);
root->left->right->left->left = GenerateBTNode(32);
root->left->right->left->right = GenerateBTNode(25);
root->left->right->right = GenerateBTNode(28);
root->right->left = GenerateBTNode(20);
root->right->right = GenerateBTNode(22);
bool flag = isFullTree(root);
cout<< flag <<endl;
displayTreeInorder(root);
}
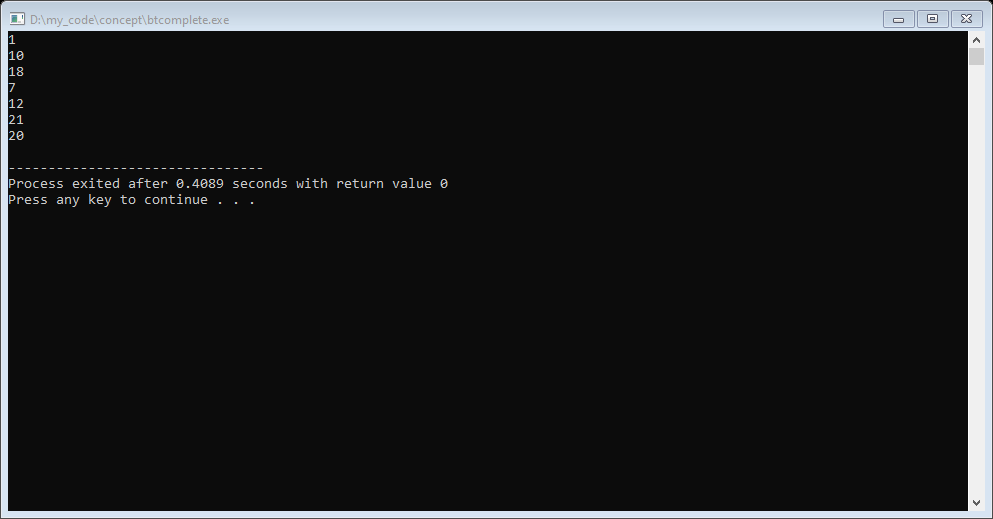
Output:
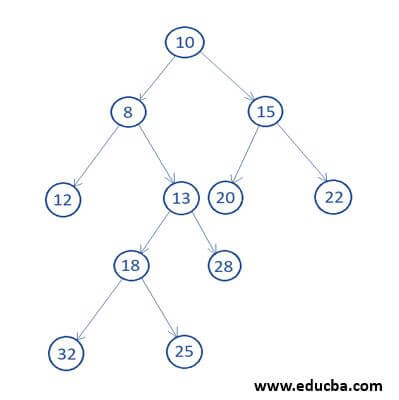
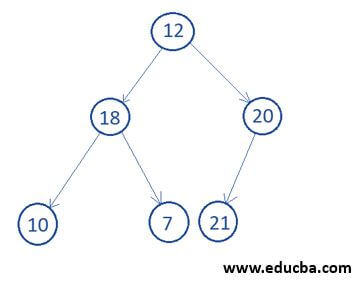
2. Complete Binary Tree
Complete Binary Tree is those binary trees in which all the levels of the tree are completely filled, the last level of the binary tree may or may not be completely filled, but in the last level of the node, each node should be at the leftmost position.
Now, Let’s check whether the above binary tree completes the binary tree or not. In the below code for checking the complete binary tree, first, get the total number of nodes. So, any node in a complete binary tree should not have an index greater than a total number of nodes. So, if we found any node in which the index is greater than a total number of nodes, then the binary tree is not a complete binary tree, and we simply return False.
Code:
struct BTNode
{
int value; // element value
struct BTNode * left; //To store address of left child
struct BTNode * right; //To store address of right child
};
struct BTNode *GenerateBTNode(int data) {
struct BTNode *node = new BTNode;
node->value = data;
node->right = NULL;
node->left = NULL;
return node;
}
int TotalBTNodes(BTNode* root) {
if (root == NULL) {
return (0);
}
return (1 + TotalBTNodes(root->left) + TotalBTNodes(root->right));
}
bool isCompleteTree( BTNode* root, int totalnode, int ind) {
if (root == NULL) {
return true;
}
if (ind >= totalnode) {
return false;
}
return (isCompleteTree(root->left, totalnode, 2*ind+ 1 ) && isCompleteTree(root->right, totalnode, 2*ind + 2));
}
void displayTreeInorder (struct BTNode *root) {
if(root != NULL){
displayTreeInorder(root->left);
cout<<root->value<<endl;
displayTreeInorder(root->right);
}
}
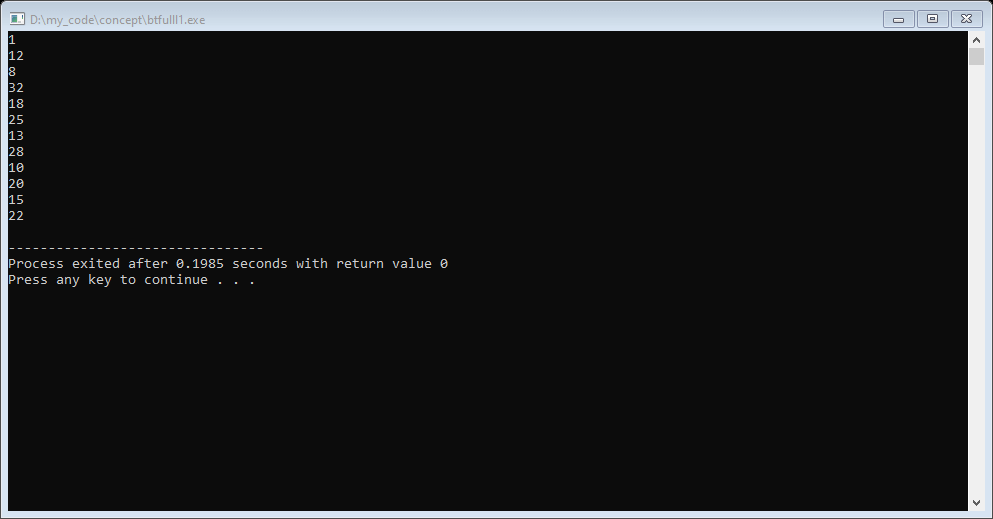
int main(){
BTNode *root=NULL;
root = GenerateBTNode(12);
root->left = GenerateBTNode(18);
root->right = GenerateBTNode(20);
root->left->left = GenerateBTNode(10);
root->left->right = GenerateBTNode(7);
root->right->left = GenerateBTNode(21);
int totalnode = TotalBTNodes(root);
bool flag = isCompleteTree(root, totalnode, 0);
cout<< flag <<endl;
displayTreeInorder(root);
}
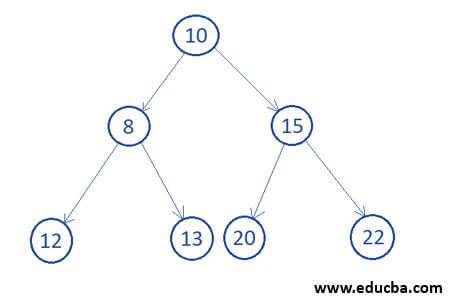
Output:
3. Perfect Binary Tree
Perfect Binary Tree is those binary trees in which each node should have two children or no children, and the level of each leaf node should be the same. The level of a node is the height or distance from the root node. A perfect binary tree is a complete binary tree in which their last level is also completely filled.
4. Balance Binary Tree
Balance Binary Tree is those binary trees in which the height of binary is log2 of the total number of nodes in that binary tree. Let the h is the height of the tree and n is the number of nodes of the tree. Then h = log(n).
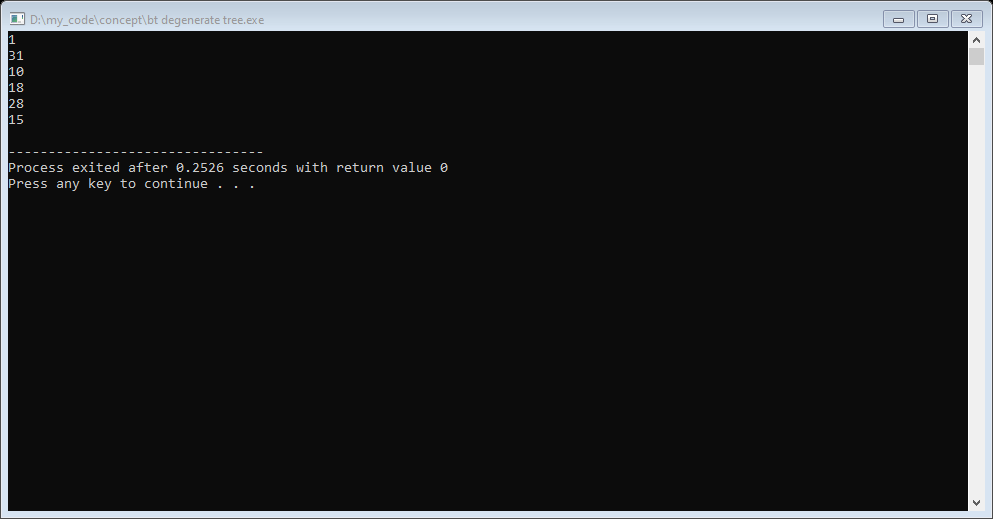
5. Degenerate Binary Tree
A degenerate Binary Tree is that binary in which each has only one child. It can be left children or right children, but any node should not have both children.
Code:
struct BTNode
{
int value; // element value
struct BTNode * left; //To store address of left child
struct BTNode * right; //To store address of right child
};
struct BTNode *GenerateBTNode(int data) {
struct BTNode *node = new BTNode;
node->value = data;
node->right = NULL;
node->left = NULL;
return node;
}
bool isDegenerateTree(struct BTNode *root) {
if(root == NULL){
return true;
}
if(root->left == NULL && root->right == NULL){
return true;
}
// If root have two children
if(root->left!=NULL && root->right!=NULL){
return false;
}
if(root->left != NULL){
return(isDegenerateTree(root->left));
}
else{
return(isDegenerateTree(root->right));
}
}
void displayTreeInorder (struct BTNode *root) {
if(root != NULL){
displayTreeInorder(root->left);
cout<<root->value<<endl;
displayTreeInorder(root->right);
}
}
int main(){
BTNode *root=NULL;
root = GenerateBTNode(15);
root->left = GenerateBTNode(31);
root->left->right = GenerateBTNode(28);
root->left->right->left = GenerateBTNode(18);
root->left->right->left->left = GenerateBTNode(10);
bool flag = isDegenerateTree(root);
cout<< flag <<endl;
displayTreeInorder(root);
}
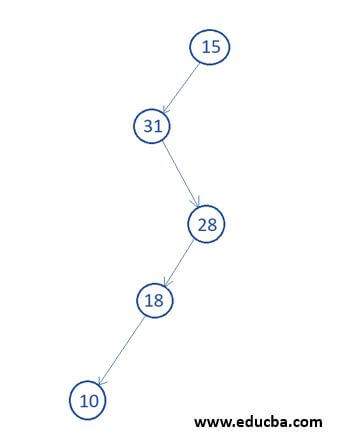
Output:
Conclusion
These all are the types of Binary trees. Therefore, studying different types of Binary trees will help us perform better operations in better Time complexity.
Recommended Articles
This is a guide to Binary Tree Types. Here we discuss the different types like full, complete, perfect, balance, and degenerate Binary Tree in a data structure. You may also look at the following articles to learn more –