Updated March 6, 2023
Introduction to Binary Tree vs Binary Search Tree
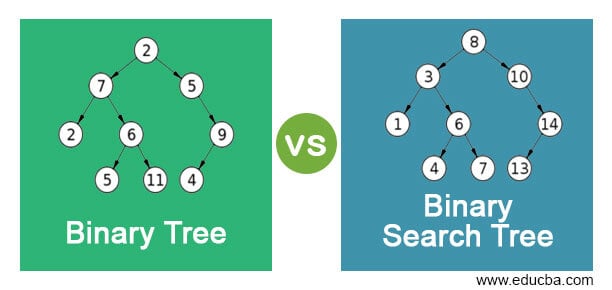
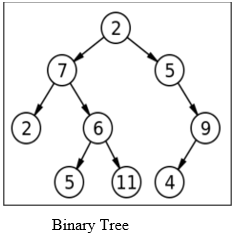
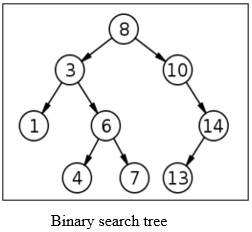
A tree data structure where we have different nodes which are commonly referred to as child nodes that can be used for computational programming is called a Binary tree. We can access the nodes based on some value or any label. Also, this can be used as the representation of data for a bifurcating structure. Binary search tree is a sorted binary tree where binary searches can be done for faster results or in computational terms, for a faster lookup. We have different variants in the binary search tree and each has different orders to be sorted.
Head to Head Comparison Between Binary Tree vs Binary Search Tree (Infographics)
Below are the top 8 differences between Binary Tree vs Binary Search Tree:
| Binary tree | Binary search tree |
| As it does not have any specific condition for its child nodes, it is useful in representing a hierarchical structure and not an ordered structure. Ancestral family hierarchy is an example of binary tree. | Binary search tree can be used to represent both hierarchical structure and an ordered structure based on its child node conditions. |
| Since there is no ordering of data in Binary tree, duplicate values are allowed here. | There is an ordering of data. The value of the left node must be smaller than the parent node and the value of the right node must be higher than the parent node. This applies to subtrees as well. Hence, duplicate values are not allowed here. |
| We can perform operations on Binary tree but it takes longer time than binary search tree as the nodes are not in an ordered manner. The operations can be search, update, insert or delete. | The operations done on Binary search tree is done in a faster manner be it delete, update, insert or search because of the ordering of nodes. Lookups are done easily in binary search trees. |
| The top node is called the root node which has left and right pointer. Left pointer has an address of the left subtree and right pointer has right subtree. | This itself is a subtree of binary tree. Only difference is in the ordering of right and left nodes. The organization is the same as binary tree with a root node, left, and right nodes. |
| We can edit the values in nodes as per our need and still, it remains as a binary tree. | If we edit the values of the binary search tree, it is important to check whether the values still meet the condition of left and right nodes. If not, it will be reduced to a binary tree. |
| Rooted trees, full binary tree, degenerate tree, perfect and complete binary trees are the types of binary trees. If the height of binary tree ‘h’ has ‘2h-1’ nodes, it is called perfect binary tree. | The types of binary search tree are Red-black trees, T-trees, Splay trees, and AVL trees. All these trees have a relative order in the arrangement of nodes. |
| We cannot say all Binary trees are binary search trees. Some may follow the condition but some may not. | All Binary search trees are binary trees as it is the subset of binary trees and whether the condition is met, it is a binary tree always. |
| The only condition for a binary tree is that the child nodes must be of number two. | There are two main conditions in a binary search tree. The child nodes must be two and the left node should have values less than parent. Right nodes should have values greater than parent node. |
Key Differences of Binary Tree vs Binary Search Tree
The structure of both Binary tree and Binary search tree is the same but Binary tree is not ordered like Binary search tree. The data can be any type, be it numbers or strings in Binary tree. Also, if the node is on the left side, it is called the left child and if it is on the right side, it is called right child. The left child and right child of Binary search tree have conditions. Left child value should be less than parent node and right child value should be greater than the parent node. These conditions are not applicable in Binary tree.
In binary tree, the subtrees can be moved from left to right or vice versa without any calculations or ordering. This cannot be done in binary search tree. Even if we calculate the data in the nodes, it will not be correct to move left to right due to the constraints. Binary search tree is the perfect version of data tree to do lookups in data and to sort data in an efficient manner. Insertion and deletion of data also happen faster than a binary tree.
Binary search is used in algorithms where we search a specific item in the entire tree where the arrays are sorted. The search can happen only on sorted arrays. Binary search tree is otherwise called a sorted or ordered tree because the search can happen easily over here for any values. This binary search cannot be done on binary trees as it is not ordered.
Ordered operations are efficiently supported in both binary and binary search trees with search, insert, and traversal operations. It is not restricted that binary tree must be unordered always and thus any kind of operations can be done in binary tree. If the operation is ordered, then it can be done on the subtrees of binary search trees.
When we do the traversal operation on a binary tree and if it is in unordered form, we get a binary search tree. The traversal operation on binary tree need not be in any order as it takes all forms of traversal.
Binary search tree, perfect binary tree, full binary tree, etc. are formed from the base of a binary tree structure. Balanced binary search trees such as 2-3 trees, red-black trees, etc. are formed from binary search trees. Most of these trees are height-balanced.
Binary search trees purpose is to optimize and manage the search operation while doing the lookup activity and this succeeds greatly in that purpose. Binary trees formed the base and now the advantages of binary search trees and balanced trees are astonishing in the programming world.
Recommended Articles
This is a guide to Binary Tree vs Binary Search Tree. Here we discuss the Binary Tree vs Binary Search Tree key differences with infographics and comparison table, respectively. You may also have a look at the following articles to learn more –