Updated November 23, 2023

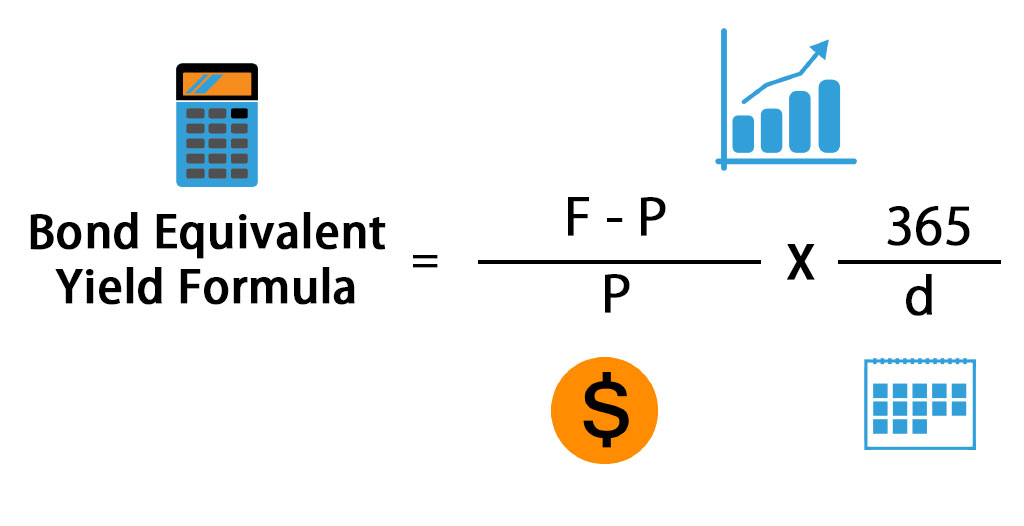
Bond Equivalent Yield Formula

A company has only two primary funding sources: Debt and Equity. Equity represents the money raised by issuing company shares, which grants ownership rights to the shareholders. However, it is considered a relatively expensive source of funds because equity owners expect higher investment returns. They bear the risk of being the last to receive returns after all other parties, including debt holders, have been paid. Sometimes, this can result in no returns if the company fails.

On the other hand, Debt is a cheaper source of funds for the company. Debt holders receive a fixed interest on the money they lend and are considered safer than equity holders because they are prioritized for payment in case the company fails. However, having a very high debt level increases the fixed commitment of the company. If these commitments are not paid on time, it may lead to bankruptcy, which is not true with equity.

Hence, every company requires a proper mix of Debt and Equity to run the company efficiently. There are various means of raising debt Bank borrowings, Non-Convertible Debentures, Bonds, Zero Coupon Bonds, Convertible Debentures, etc. Although, In India, Bonds and Debentures are similar and often used interchangeably, they have different characteristics in some markets, like the U.S.

Companies issue different bonds with varying tenures, interest rates, and payment schedules to meet their requirements. They pay interest every quarter, half-yearly, or annually. Zero-coupon bonds, however, pay interest directly at bond maturity. For discount bonds that do not make annual payments, bringing them to the same level as other fixed-income securities with annual payments is necessary. This is achieved by utilizing the Bond Equivalent Yield Formula. This formula annualizes the bond’s return, enabling easy comparison and selection of the best investment option.

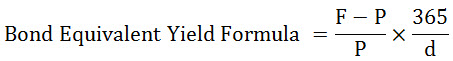
Here’s the Bond Equivalent Yield Formula –

Where,

F = Face Value
P = Purchase Price of the bond
d = Duration of Bond/Days to Maturity

So, a Bond Equivalent Yield Formula is calculated by dividing the difference between the Face Value and the bond’s purchase price by the bond’s purchase price, multiplying it by 365, and dividing it by the number of days to maturity. The first part of the formula is for calculating the return on investment, and the second part is used to annualize the return.

Examples

Let’s take an example to find out the Bond Equivalent Yield for a company: –

You can download this Bond Equivalent Yield Formula Template here – Bond Equivalent Yield Formula Template

Example #1

Mr. Amar is evaluating two bonds for investors. Bond A is Rs. 95 (Face Value Rs. 100) for 3 months, and Bond B is Rs. 90 (Face Value Rs. 100) for 6 months. Which one should Mr. Amar choose?

This is a common scenario of being confused in choosing different bonds with different prices and tenure. Hence, we use the Bond Equivalent Yield to calculate and compare both bonds’ annualized yields to resolve this issue.

Let’s calculate the Bond Equivalent Yield for both bonds to reach a conclusion:

Bond Equivalent Yield = [{(Face Value – Purchase Price)/ Purchase Price}*{365 (or 12)/Days(or Months) to Maturity of Bond}]

Bond A = [{(100- 95)/95}*{12/3}]
Bond A = [{(5)/95}*{4}]
Bond A = [{0.052632}*{4}]
Bond A = 0.210526 or 21.1%

Now, we will find out the Bond B

Bond B = [{(100-90)/90}*{12/6}]
Bond B = [{(10)/90}*{2}]
Bond B = [{0.111111}*{2}]
Bond B = 0.222222 or 22.2%

Based on the above comparison, as we could witness, Bond B is giving a higher annualized yield. Hence, Mr. Amar should choose to invest in Bond B.

Explanation

As stated in the above example, Mr. Amar is confused about choosing between Bond A and B to invest his money. The Face Value of both bonds is the same i.e. Rs. 100. However, Bond A is available at a Rs.5 discount while Bond B is available at a Rs. 10 discount. In terms of tenure, the Tenure of Bond A is 3 months while that of Bond B is 6 months i.e. post the respective time, bonds will mature, and the investor will receive back the Face Value of the Bond, in this case, Rs. 100. You could also refer the excel sheet to understand how Bond Equivalent Yield is calculated in Excel.

Example #2

Piramal Capital is willing to invest Rs. 1000 Cr in fixed-income government securities. They are evaluating two securities for investment; the first government security is a 180-day bond with a Face Value of Rs. 100 and currently selling at Rs. 98, and the second government security is a 240-day government security with a Face Value of Rs. 100 and currently selling at Rs. 95.

Now, to conclude upon which security to choose for investment, Piramal Capital used the Bond Equivalent Yield Formula and calculated the yield of both securities as mentioned below:

Bond Equivalent Yield = [{(Face Value – currently selling)/ currently selling}*{365 /Days}]

Bond Equivalent of Yield of First Govt. Security

Bond Equivalent Yield of First Govt. Security = [{(100-98)/98}*{365/180}]
Bond Equivalent Yield of First Govt. Security = [{(2)/98}*{2.027778}]
Bond Equivalent Yield of First Govt. Security = [{0.020408}*{2.027778}]
Bond Equivalent Yield of First Govt. Security = 0.041 or 4.1%

Now, we must find the Bond Equivalent of the Yield of the Second Govt. Security by using the above formula

Bond Equivalent of Yield of Second Govt. Security = [{(100-95)/95}*{365/240}]
Bond Equivalent of Yield of Second Govt. Security = [{(5)/95}*{1.520833}]
Bond Equivalent of Yield of Second Govt. Security = [{0.052632}*{1.520833}]
Bond Equivalent of Yield of Second Govt. Security = 0.08 or 8%

Based on the comparison using the Bond Equivalent Yield, it was clear to invest in the Second Govt. Bond has a higher annual yield compared to First Govt. Security.

Example #3

An investor has Rs. 1 crore, which he wants to invest in fixed-income securities. He has filtered various investment options and has shortlisted two securities: one is NCD of Tata Capital with an annualized yield of 13%, and the other is a ZCB of Indian Railways, which is selling at a discount of 5% at Rs. 95 per unit with Face Value Rs. 100. Tenure of ZCB is 120 days.

To reach a conclusion, the Investor uses the Bond Equivalent Yield to calculate the annualized yield of the ZCB and compare it with the annualized yield of the NCD of Tata Capital.

Bond Equivalent Yield = [{(Face Value – Purchase Price)/ Purchase Price}*{365 (or 12)/Days}]

Bond Equivalent Yield of ZCB = [{(100-95)/95}*{(365/120)}]
Bond Equivalent Yield of ZCB = [{(5)/95*{(3.041667)}]
Bond Equivalent Yield of ZCB = [(0.052632)*(3.041667)]
Bond Equivalent Yield of ZCB = 0.16 or 16%

An annualized yield of ZCB is higher than the NCD. The investor invests Rs. 1 crore in ZCB of Indian Railways.

Significance and Use of Bond Equivalent Yield Formula

Bond Equivalent Yield is relevant and useful for investing in fixed-income securities. However, this formula is primarily used for fixed-income securities, which are being sold at a discount and do not offer any annual payments.

An investor can use this formula to compute the annual yield of such bonds and compare it with the annual yields of other available options to choose the best among all.

Bond Equivalent Yield Formula Calculator

You can use the following Bond Equivalent Yield Formula Calculator

Face Value
Purchase Price of the Bond
d
Bond Equivalent Yield Formula =

Bond Equivalent Yield Formula =

Face Value - Purchase Price of the Bond		365
	X
Purchase Price of the Bond		d

0−0		365
	X		=	0
0		0

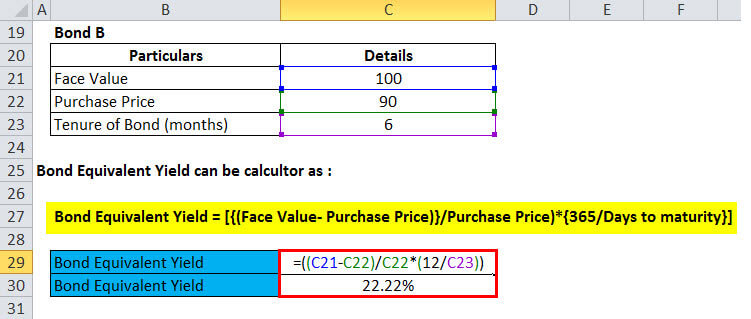
Bond Equivalent Yield Formula in Excel (With Excel Template)

Here, we will do the above example of the Bond Equivalent Yield Formula in Excel. It is very easy and simple. You need to provide the three inputs, i.e, Face Value, Purchase Price of the bond, and Duration of Bond/Days to Maturity

Here first, we have found out the Bond Equivalent Yield for Bond A