Introduction to Constraint Satisfaction Problems in AI
Imagine a tireless assistant who can create conflict-free work schedules for your entire team, ensure no two events clash on your calendar, or even generate a perfectly balanced Sudoku solution in seconds. That’s the power of CSPs in action. They act as a sophisticated rulebook for AI, defining the variables (think puzzle pieces) and the restrictions (the rules) governing how these pieces interact. The ultimate goal? To find the perfect arrangement where all the pieces fit together seamlessly, satisfying every constraint.
Intrigued? Let’s embark on a journey to explore the magic of CSPs and how they’re revolutionizing the way AI tackles real-world challenges!
Table of Contents
What is a Constraint Satisfaction Problem (CSP)?
Constraint satisfaction problems (CSPs) are essential in artificial intelligence as they model situations where one must make choices while adhering to predetermined limitations. Many areas utilize CSPs for applications, including resource allocation, planning, and scheduling. The aim is to find a solution that satisfies every requirement. Constraints, variables, and domains define CSPs, and finding workable solutions calls for effective algorithms like constraint propagation or backtracking. Comprehending CSPs is essential to creating AI systems that work well.
Key Takeaways
- The foundation of AI (artificial intelligence) is the solution to constraint satisfaction problems (CSPs), which require satisfying constraints.
- CSP finds applications in planning, scheduling, and resource allocation.
- These include variables, domains, and constraints and require efficient algorithms such as backtracking to find solutions.
- Understanding CSP is essential for developing effective AI systems.
Key Components of CSPs
- Variables: In solving the problem, one must ascertain the values of the entities represented by the variables in CSPs. These variables may represent various things, such as judgments to make, allocated resources, or work to organize. Typically, each variable has a designated domain of values to access.
- Domains: Domains specify the range of potential values for variables. For instance, a variable representing the days of the week might have Monday, Tuesday, Wednesday, and so on as its domain. Depending on the nature of the problem, Domains can be infinite or finite, discrete or continuous.
- Constraints: These are limitations or requirements that must be met by the values assigned to the variables. They restrict the range of values supplied to them and specify the relationships between various variables. Restrictions can be classified as higher-order, binary, or unary based on whether one, two, or more variables are involved.
- Solution Space: The solution space of a CSP contains every possible combination of variable assignments that satisfies every constraint. It represents every possible fix for the issue. But not every combination in the solution space is a legitimate solution; it has to fit within the given parameters.
- Search Algorithms: CSPs frequently require a systematic investigation of the solution space to identify workable solutions. Various search strategies, including local search, constraint propagation, and backtracking, navigate the solution space and locate appropriate variable assignments effectively. By shrewdly removing inconsistent or impractical assignments, these algorithms aim to make the search space smaller to either find a solution or conclude that none exists.
Problem Formulation
CSP Scheduling
- Problem: Efficiently schedule employee shifts considering their availability, preferences, and organizational rules, aiming for compliance and maximizing satisfaction and operational efficiency.
- Variable: Shift assignment for each employee.
- Domain: Time slots available for each shift.
- Restrictions: These include employee availability, preferences, and legal or organizational rules such as maximum working hours and consecutive days off.
Planning CSP:
- Problem: Plan a robot’s path through a warehouse to pick up and deliver items efficiently.
- Variables: robot position and motion at each time step.
- Domain: Possible locations and actions (e.g., move left, move right, pick up, drop off).
- Constraints: Obstacle avoidance, resource limitations (e.g., battery life), and task dependencies (e.g., receiving items before delivery).
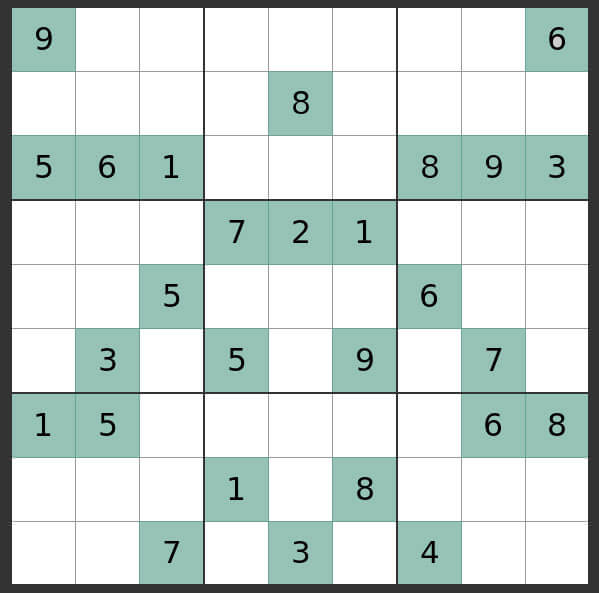
Sudoku CSP:
- Problem: Solve a Sudoku puzzle where each row, column, and 3×3 subgrid must contain all numbers from 1 to 9 without repeating.
- Variable: Value assigned to each cell in the Sudoku grid.
- Domain: Number from 1 to 9.
- Constraint: Each value must be unique within its row, column, and 3×3 subgrid.
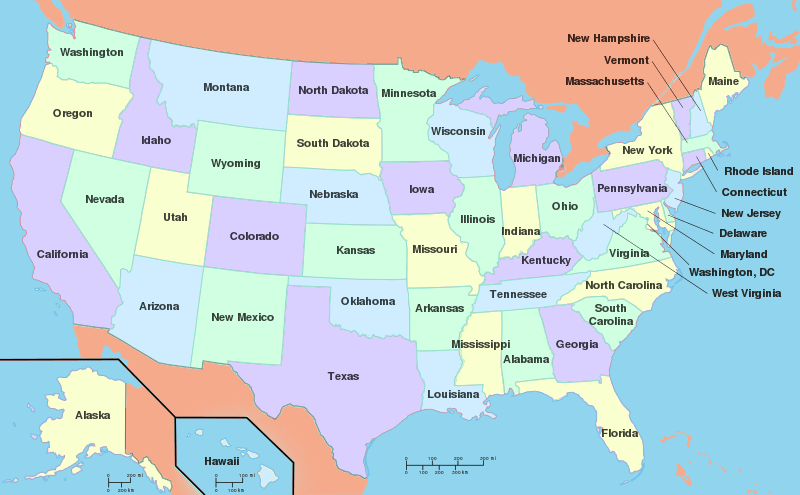
Coloring the Map CSP:
- Problem: Color the map with the minimum number of colors so that adjacent areas do not have the same color.
- Variables: Region on map.
- Domain: Colors available for each region.
- Restriction: Adjacent areas must be different colors.
N-Queens CSP:
- Problem: Assume that no two queens may pose a threat to one another while placing N queens on a N × N chessboard.
- Variables: Queen’s position on the chessboard.
- Domains: Rows and columns of a chessboard.
- Restriction: There cannot be two queens in the same row, column, or diagonal.
Implementation of CSP in AI
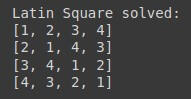
Let’s solve a Latin Square puzzle using backtracking. A Latin Square is an n×n grid filled with numbers such that each row and each column contains every number from 1 to n exactly once.
Code:
def is_valid(row, col, value, square):
"""Checks if assigning 'value' to cell (row, col) violates constraints."""
# Check row and column for duplicates
for i in range(n):
if square[row][i] == value or square[i][col] == value:
return False
return True
def solve_latin_square(n, square):
"""Solves the Latin Square puzzle using backtracking."""
# Find an empty cell
for row in range(n):
for col in range(n):
if square[row][col] == 0:
# Try assigning values 1-n to the empty cell
for value in range(1, n + 1):
if is_valid(row, col, value, square):
square[row][col] = value
if solve_latin_square(n, square): # Recursively solve with the assignment
return True
square[row][col] = 0 # Backtrack: remove assigned value
return False # No valid value found for this cell (dead-end)
# All cells are filled, solution found
return True
# Example usage: Define the size (n) and an empty square
n = 4
square = [[0 for _ in range(n)] for _ in range(n)]
# Solve the puzzle
if solve_latin_square(n, square):
print("Latin Square solved:")
for row in square:
print(row)
else:
print("No solution found for the given Latin Square size.")Output:
Explanation:
- Functionality: The code solves Latin Square puzzles using backtracking.
- is_valid Function: Checks if assigning a value to a cell violates constraints by ensuring the value is not already present in the row or column.
- solve_latin_square Function: Iterates through each cell, attempting to assign values recursively, backtracking if necessary.
- Example Usage: Defines the size of the Latin Square, initializes an empty square, and solves the puzzle.
Types of Domains in CSP
Finite Domains: These domains consist of a finite set of discrete values. They are frequently employed when variables have a finite set of possible values. Discrete choices, like days of the week, colors, or integer values within a range, are best represented by finite domains. For instance, in a scheduling problem, discrete hours or minutes throughout the day can make up the domain for a variable representing time slots.
Example: In a scheduling problem, the domain for a variable representing time slots could consist of discrete hours or minutes throughout the day, such as {8:00 AM, 9:00 AM, 10:00 AM, …, 5:00 PM}.
Infinite Domains: An infinite domain, as opposed to finite domains, can contain an infinite number of possible values. Continuous optimization problems in which variables can take on any real value within a given range typically involve these topics. Infinite domains are necessary when modeling continuous phenomena like temperature, distance, or time in problems like resource allocation or trajectory planning.
Example: In trajectory planning, the domain for a variable representing the position of a moving object might be infinite, as it can take any real value within a given range, such as all possible coordinates in a continuous space.
Enumerated Domains: Enumerated domains explicitly list all possible values variables can take. They are commonly used in problems where the set of feasible options is well-defined and finite. For instance, in a Sudoku puzzle, the domain for each cell consists of the numbers 1 through 9. By explicitly specifying the valid choices for each variable, enumerated domains simplify problem representation and solution.
Example: In a Sudoku puzzle, each cell’s domain consists of the numbers 1 through 9, explicitly listing all possible values the cell can take.
Interval Domains: They describe the possible values that variables can have. They are especially helpful in situations when the variables’ domains are ordered or continuous. For instance, in a resource allocation problem, an interval from a minimum to a maximum value could be the domain for a variable indicating quantities of a resource. Interval domains limit the possible range of values while offering flexibility in describing continuous or indeterminate quantities.
Example: In a resource allocation problem, the domain for a variable representing quantities of a resource could be an interval from a minimum to a maximum value, such as [0, 100], indicating the possible range of resource quantities available for allocation.
Composite Domains: Composite domains are formed by combining multiple simpler domains. They represent complex relationships between variables or capture dependencies among different aspects of the problem. In planning or optimization problems, composite domains might combine an agent’s possible locations and actions at each time step. By integrating multiple dimensions of variability, composite domains enable the modeling of intricate decision spaces.
Example: In a planning problem involving an agent’s movement and actions, a composite domain could combine the agent’s possible locations and actions at each time step, integrating spatial and action dimensions to represent complex decision spaces. For instance, the domain might include pairs of (location, action) tuples for each time step.
Problem Representation
Consider a classic example of a Constraint Satisfaction Problem (CSP) – the N-Queens problem.
Problem Statement: Given an N×N chessboard, the N-Queens problem is placing N queens on the board so that no two queens threaten each other. Specifically, no two queens should share the same row, column, or diagonal.
Representation:
- Variables (X):
- In the N-Queens problem, each variable represents a column on the chessboard.
- Each variable corresponds to the row where you place a queen in that column. For example, if Xi=j, it means a queen is place in column i at row j.
- Domains (D):
- The set of rows where a queen can be in placed of the i-th column without violating any constraints is the domain for each variable Xi. For an N×N chessboard, the domain for each variable Xi is {1,2,…,N}.
- Constraints (C):
- The constraints ensure that no two queens threaten each other.
- The primary constraints are: a. Row Constraint: No two queens can be in place on the same row. b. Column Constraint: No two queens can be in place on the same column. c. Diagonal Constraint: No two queens can be in place on the same diagonal.
- These constraints are-enforced between pairs of variables. For any two variables Xi and Xj, where i≠=j, there are constraints to ensure that the queens placed in columns i and j do not threaten each other.
CSP Solving Algorithms
- Backtracking Search:
- Description: Backtracking is a systematic approach to exploring the search space of a CSP to find solutions.
- Process:
- Start by selecting an unassigned variable.
- Try assigning a value from its domain.
- Check if the assignment violates any constraints.
- If consistent, move to the next variable and repeat recursively.
- If inconsistency is detected, backtrack to the previous variable and try another value.
- Continue until all variables are assigned values satisfying all constraints or no solution exists.
- Use Case: Suitable for smaller CSPs where exhaustively searching the entire solution space is feasible.
- Constraint Propagation:
- Description: Constraint propagation reduces search space by enforcing constraints more efficiently through local inference.
- Process:
- Repeatedly apply constraint-specific techniques to eliminate values from variable domains.
- Example: Arc consistency removes inconsistent values by examining pairs of variables and their constraints.
- Helps in detecting and eliminating conflicts early, reducing the need for extensive backtracking.
- Use Case: Useful in reducing search space for larger CSPs, potentially avoiding unnecessary exploration.
- Local Search:
- Description: Local search algorithms iteratively improve a solution by making small changes and evaluating their impact on satisfying constraints.
- Process:
- Start with an initial assignment.
- Iteratively modify the assignment, evaluating solution quality based on constraint satisfaction.
- Examples include hill climbing, simulated annealing, and genetic algorithms.
- Use Case: Suitable for large and complex CSPs where exhaustive search methods like backtracking are not practical due to computational constraints.
Applications of CSPs
Various fields have applied constraint satisfaction problems (CSPs) because they are versatile in modeling and solving different problems. Common uses include:
- Scheduling: CSP, used for scheduling tasks, appointments, and resources in manufacturing, transportation, healthcare, and project management. These help optimize resource utilization, minimize idle time, and meet constraints like deadlines and availability.
- Planning: CSP plays an important role in planning the activities of autonomous agents, robots, and vehicles. They help determine optimal paths, sequences of actions, and resource allocation, considering constraints such as obstacles, task dependencies, and resource limitations.
- Resource Allocation: CSP efficiently allocates resources such as personnel, equipment, and funds. They help enterprises optimize resource utilization, balance workload distribution, and allocate resources based on priorities and constraints.
- Cryptography: CSP is used in cryptographic applications to solve puzzles, decipher codes, and decrypt encrypted messages. These help find solutions that satisfy cryptographic constraints, such as key combinations and encryption algorithms.
- Bioinformatics: CSP is used in bioinformatics to analyze biological data, design experiments, and predict molecular structure. These are useful for solving combinatorial optimization problems such as sequence alignment, protein folding, and gene regulatory network inference.
Advanced Topics
- Hybrid CSP Solvers:
- Hybrid CSP solvers tackle complex CSPs more successfully by combining many approaches or methods.
- These solvers frequently incorporate heuristics tailored to the problem, constraint propagation techniques, or search strategies.
- A hybrid solver might combine constraint propagation strategies like arc consistency or forward checking with a backtracking search.
- Hybrid CSP solvers can tackle complex problems with greater performance and scalability by combining the advantages of several methods.
- Dynamic CSPs:
- Dynamic CSPs extend traditional CSPs by allowing the problem’s structure or constraints to change over time.
- Variables, domains, and restrictions in dynamic CSPs can be dynamically added, withdrawn, or altered in response to outside events or shifting issue circumstances.
- These issues frequently surface in dynamic settings like online decision-making systems, adaptive resource allocation, and real-time scheduling.
- Algorithms that can effectively adjust to changes in the problem instance while preserving consistency and optimality are needed to solve dynamic CSPs.
- Soft Constraints:
- Soft constraints relax stringent satisfaction in CSPs., which permit partial satisfaction or trade-offs between competing demands.
- Unlike typical CSPs, soft constraints introduce preferences or penalties associated with constraint breaches, where solutions must fully fulfill all constraints.
- Soft constraint satisfaction aims to identify solutions that minimize soft constraint violations while maximizing overall satisfaction.
- People frequently apply these methods to preference modeling, optimization under uncertainty, and decision-making scenarios where discovering a perfect answer might not be essential or practical.
Conclusion
Constraint Satisfaction Problems (CSPs) are vital in AI, facilitating versatile problem-solving across domains. With efficient algorithms, CSPs enable effective decision-making and optimization. Their significance spans scheduling, planning, and beyond, showcasing their pivotal role in real-world applications and advancing artificial intelligence capabilities.
FAQs
Q1. What are soft constraints in CSPs?
Answer: Soft constraints relax the notion of strict satisfaction and allow for partial satisfaction or compromise between conflicting constraints. They are often used in preference modeling and decision making under uncertainty.
Q2. What are some techniques to handle constraints in CSPs?
Answer: The techniques include constraint propagation to reduce the search space, heuristic methods to order variables and values, and intelligent backtracking strategies to explore promising branches of the search tree first.
Q3. Can CSPs handle uncertainty and incomplete information?
Answer: Yes, Techniques like probabilistic inference or soft constraints can extend CSPs to handle uncertainty, enabling flexible decision-making in uncertain environments.
Recommended Articles
We hope that this EDUCBA information on “Constraint Satisfaction Problems in AI” was beneficial to you. You can view EDUCBA’s recommended articles for more information,