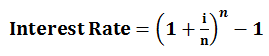Updated August 1, 2023
Definition of Effective Interest Rate
There are multiple options in the financial market regarding investment products and loan opportunities. Our final decision-making process is ultimately influenced by the extent of interest implied on various financial instruments as we explore options that offer better returns or loans with minimum interest rates. The correlation between these factors guides our decision-making.
The “Effective Interest Rate” is the subtle way of comparing these instruments where we can deduce and finally decide whether to go ahead with a loan/investment.
Most importantly, it clarifies and evaluates the outcome where compounded interests are levied differently. It should be noted that the nominal interest rate is the simplest interest rate, also called a stated interest rate. There are no fundamentals such as compounding for the stated interest rate, which differs from an effective interest rate (EIR).
Compound interest is calculated based on the principal amount but includes all the accrued interest of previous periods of a loan or investment. It can, therefore, be term as‘ interest on interest’ and can enormously grow the sum faster than how it goes with a stated interest rate calculated by principal amount only. The rate of compounding interest being accrued depends upon the compounding frequency, so the more compounding periods, the higher the compounding interest.
The Formula of Effective Interest Rate
To understand the concept of Effective Interest Rate, the calculation can be carried out with the below formula:
- i = Annual rate of interest
- n = number of the compounding period
Example
Let’s take an example of a 1-year investment through Bank X and Bank Y for $10k with below-compounding interest periods:
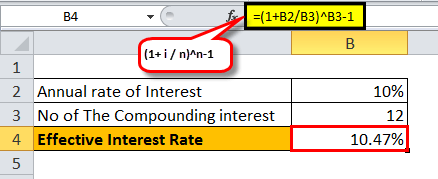
- Bank X pays 10%, compounded monthly:
- In this case, we have i = 10%, n = 12 [as its compounded monthly]
= ((1+(10%/12)^12)-1
=10.47%
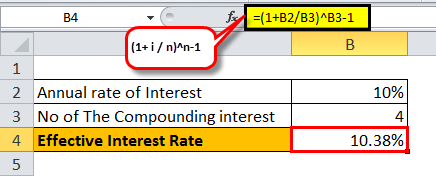
- Bank Y pays 10.3%, compounded quarterly:
- In this case, we have i = 10%, n = 4 [as its compounded quarterly]
= ((1+(10%/4)^4)-1
=10.38%
As we can see, the effective interest rate varies for a different set of compounding periods. The more compounding occurs in one year, the more effective the interest rate would accrue.
Below is the description for a 10% interest rate with increasing compounding frequency in one year:
Importance
Below is what we can trace down as per the above to understand it better
- Help to secure a worthful investment – Now that we comprehend the impact of interest rates and compounding, we can confidently make informed investment decisions, free from the influence of social media advertisements and blindly trusting their strategies. It allows us to avoid the uncertainty that could hinder our earning expectations.
- Help to opt for a loan with full visibility of risk and issues- We know what the actual interest would be levied upon us annually for whatever compounding factor that loan follows. This would cause no hiccups at any point in time within the whole life of the loan.
- Enhance the way we analyze/compare financial products – Wouldn’t it give us a sigh of relief if we could conclude which investment or loan is most beneficial for us to go ahead with? Well, understanding the impact of an effective interest rate than a nominal interest rate takes you one step further ahead to healthy future planning.
- Improve the decision-making for loan/investment – Differentiating media from substance impacts returns, manages expectations, and guides financial decision-making effectively. This understanding is based on effectively grasping the concept of the effective interest rate rather than the simple one.
When banks charge interest, they consider the stated interest rate rather than the annual interest rate. Banks follow this, so it would appear to consumers as if they are paying a lesser interest rate.
For a loan with a 20% interest rate compounded monthly, the effective annual interest rate is 21.93%. However, the bank will advertise the stated rate of interest being 20% despite the effective interest rate of 21.93%.
Banks may advertise an effective interest rate instead of a stated one to make the offer more attractive to consumers.
For instance, for a deposit with a stated rate of 10% compounded monthly, the effective annual interest rate would be 10.47% which the bank will portray as is so that investors can be attracted and decide to fall in with the advertising strategy. All in all, it’s just to display what’s more favorable.
Thoroughly studying the impact of compounding on our investments or loans is crucial when considering the effectiveness of the interest rate. The financial marketplace is a labyrinth of opportunities followed by unfortunate events. However, a good outcome resides for those who swing the sword at the right place at the right time. Suppose we aim to opt for investing some portion of personal savings. Comparing each investment option and considering factors such as market conditions and specific provisions can help determine which investment pillar would yield better profits in a shorter period.
The power of compounding and drilling down the core of investment/loan, followed by the effective interest rate, gives a great insight into your overall financial status of the portfolio. The beauty of compounding describes as “the eighth wonder of the world” by Albert Einstein. When combined with compounding, investors can experience the transformative power of effective interest rates, leading to favorable outcomes.
Recommended Articles
This was a guide to the Effective interest rate. Here we talk about its formula, how to calculate an effective interest rate, an example of an effective rate, and its importance. You can also check our proposed articles:-