Updated July 31, 2023

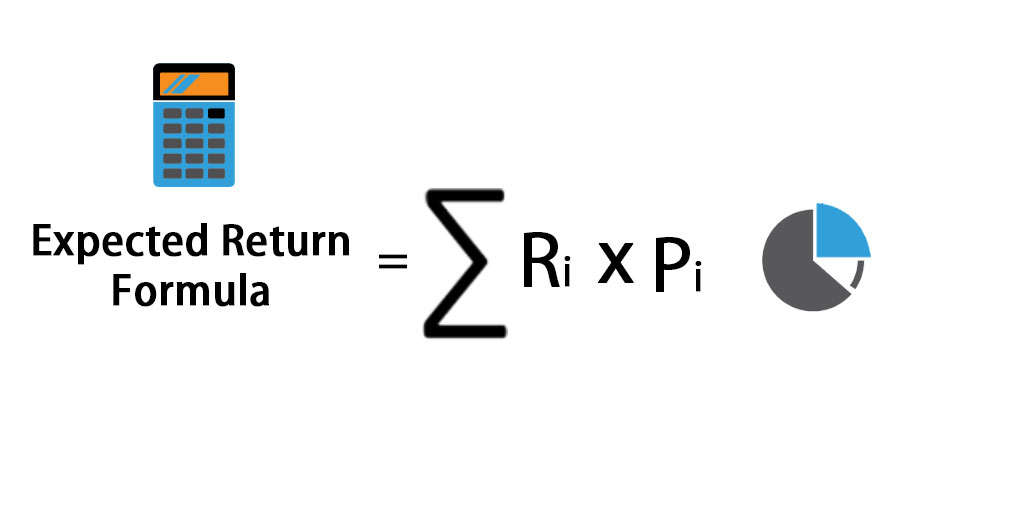
Expected Return Formula

Expected Return can be defined as the probable return for a portfolio held by investors based on past returns, or it can also be defined as an expected value of the portfolio based on the probability distribution of probable returns.

Here’s the Expected Return Formula –

Expected Return = Expected Return=∑ (R_i* P_i)

Where

R_i– Return Expectation of each scenario
P_i – Probability of the return in that scenario
i – Possible Scenarios extending from 1 to n

Examples of Expected Return Formula (With Excel Template)

Let’s take an example to understand the calculation of the Expected Return formula in a better manner.

Expected Return Formula – Example #1

Let’s take an example of a portfolio of stocks and bonds where stocks have a 50% weight and bonds weight 50%. The expected return on stocks is 15%, and the expected return for bonds is 7%.

Expected Return is calculated using the formula given below

Expected Return for Portfolio = Weight of Stock * Expected Return for Stock + Weight of Bond * Expected Return for Bond

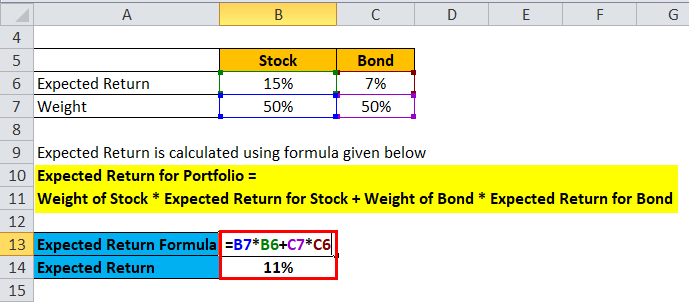
Expected Return for Portfolio = 50% * 15% + 50% * 7%
Expected Return for Portfolio = 7.5% + 3.5%
Expected Return for Portfolio = 11%

Expected Return Formula – Example #2

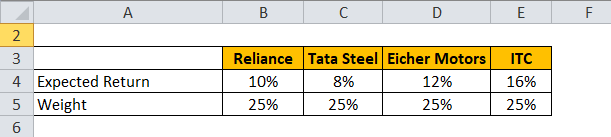
Let’s take an example of a portfolio which has stock Reliance, Tata Steel, Eicher Motors and ITC.

Expected Return is calculated using the formula given below

Expected Return for Portfolio = ∑ Weight of Each Stock * Expected Return for Each Stock

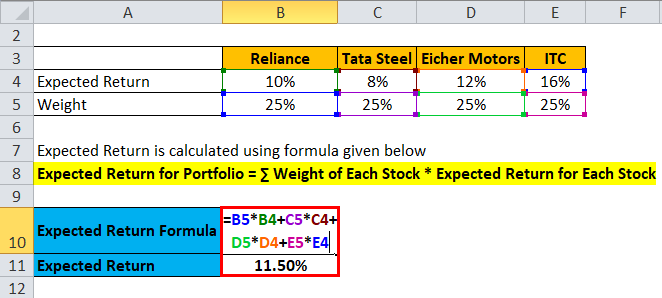
Expected Return for Portfolio = 25% * 10% + 25%* 8% + 25% * 12% + 25% * 16%
Expected Return for Portfolio = 2.5% + 2% + 3% + 4%
Expected Return for Portfolio = 11.5%

Expected Return Formula – Example #3

Let’s take an example of a portfolio of HUL, HDFC, and 10-year government bonds.

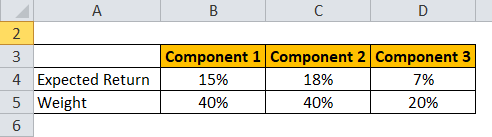
Expected Return is calculated using the formula given below

Expected Return for Portfolio = ∑ Weight of Each Component * Expected Return for Each Component

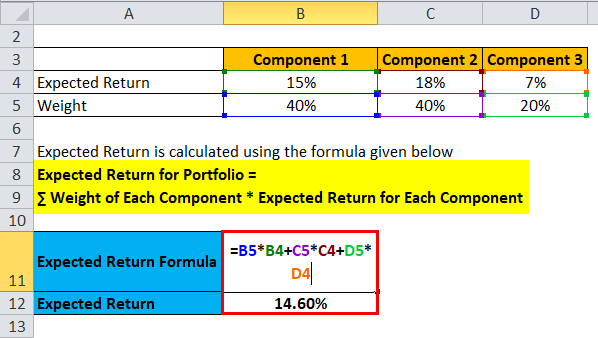
Expected Return for Portfolio = 40% * 15% + 40% * 18% + 20% * 7%
Expected Return for Portfolio = 6% + 7.2% + 1.40%
Expected Return for Portfolio = 14.60%

You can download this Expected Return Formula Excel Template here – Expected Return Formula Excel Template

Explanation of Expected Return Formula

Investors define the expected return as the probable return for a portfolio based on past returns or as the expected value of the portfolio derived from a probability distribution of probable returns. In the short term, the expected return represents a random variable that takes different values based on distinct probabilities. This random variable has values within a certain range and can only assume values within that particular range. Therefore, calculating the expected return relies on historical data and may not be reliable for forecasting future returns. It measures various probabilities, the likelihood of achieving a positive return on investment, and the value of that return.

This aims to give an investor an idea of a different level of risk and the various scenarios with different probabilities that will yield a return possibly greater than the risk-free return. As we all know, the risk-free return would be the 10-year Treasury bond yield of the United States Government.

Relevance and Uses of Expected Return Formula

As mentioned above, the Expected Return calculation is based on historical data, so it is limited in forecasting future possible returns. Investors must consider various other factors and not invest based on the calculated expected return. Take an example: –

Portfolio A – 10%, 12%, -9%, 2%, 25%

Portfolio B – 9%, 7%, 6%, 6%, 12%

If we consider both the above portfolios, both have an expected return of 8% but Portfolio A exhibits a lot of risk due to a lot of variance in returns. Investors must consider this risk, calculated by measuring Standard Deviation and Variance.

Variance- can be defined as a variation of a set of data points around their mean value. The probability-weighted average of squared deviations from the mean calculates it. It is a measure of risk that needs to be taken into account by investors.

First, calculate the mean of all returns. Then, find each return’s deviation from the mean value and square it to ensure all positive results. Once squared, multiply the squared deviations by their respective probability values to determine the variance.

Portfolio variance can be calculated from the following formula: – If there are two portfolios, A and B.

Portfolio Variance = w_A²* σ_A²+ w_B²* σ_B²+ 2 * w_A* w_B* Cov (A, B)

Where Cov (A, B) – is the covariance of portfolios A and B

Standard Deviation – It is another measure that denotes the deviation from its mean. Standard deviation is calculated by taking a square root of the variance and denoted by σ.

Expected Return Formula Calculator

You can use the following Expected Return Calculator.

R₁
P₁
R₂
P₂
R₃
P₃
R₄
P₄
Expected Return

Expected Return =	R₁P₁ + R₂P₂ + R₃P₃ + R₄P₄
	0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 =	0

Conclusion

Investors should not solely consider the expected return, defined as the probable return for a portfolio based on past returns, when deciding whether to invest. The limitations arise from its reliance on past returns. Instead, investors must examine other measures, such as the portfolio’s variance and standard deviation.