Updated July 28, 2023
Harmonic Mean Formula (Table of Contents)
- Harmonic Mean Formula
- Examples of Harmonic Mean Formula (With Excel Template)
- Harmonic Mean Formula Calculator
Harmonic Mean Basically Formula
Harmonic mean is basically a type of average used in statistics that is reciprocal of the arithmetic mean of the reciprocals. Therefore, the harmonic mean is always less than the arithmetic means of the same data set. Harmonic mean is not commonly used as arithmetic or geometric mean and is used in specific situations or when dealing with averages of units, like average travel speed and other ratios. This is also used in the area of finance to calculate price multiples like price-earnings ratio, price-sales ratio, etc. If we use weighted arithmetic mean to calculate these values, high data points will get higher weightage, and lower data points will get lower weightage which will create a problem and will not give us the right multiple.
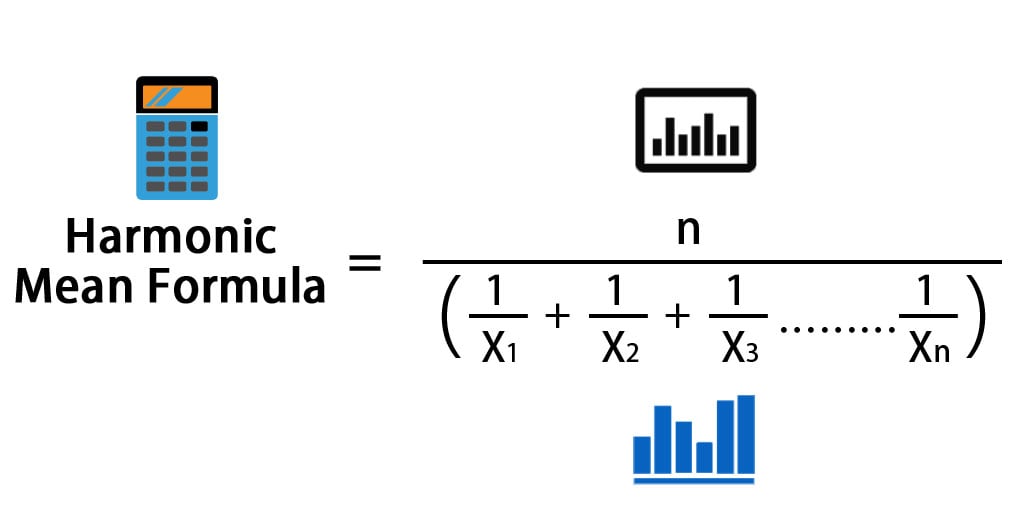
Suppose that we have a data set with n data points and is given by X: {X1, X2, X3……..Xn}.
Formula For Harmonic Mean is
Where:
- X1, X2,…Xn – Data Points
- n – Total number of data points
Steps to calculate harmonic mean:
- Take the reciprocal of all the data points in the data set.
- After that, find the mean/average of those values.
- The next and final step is to take the reciprocal of that value to arrive at a harmonic mean.
Examples of Harmonic Mean Formula (With Excel Template)
Let’s take an example to understand the calculation of Harmonic Mean in a better manner.
Harmonic Mean Formula – Example #1
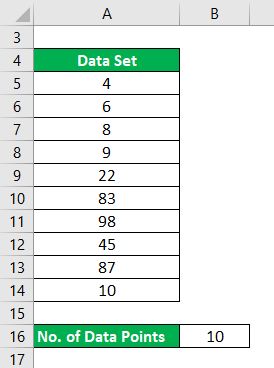
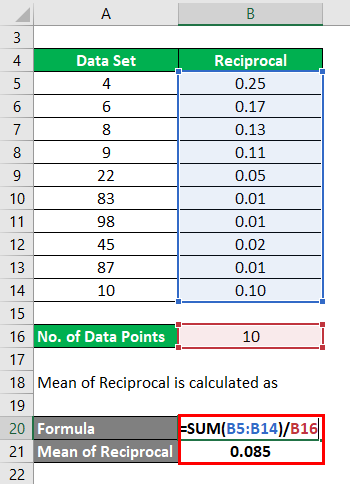
Let say you have a data set with 10 data points, and we want to calculate the harmonic mean for that.
Data Set : {4,6,8,9,22,83,98,45,87,10}
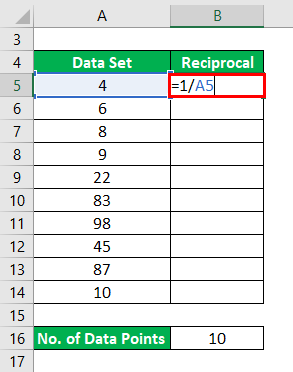
Reciprocal will be calculated as:
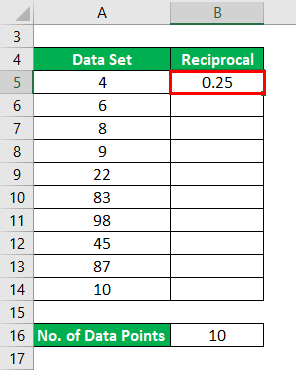
The result will be as given below.
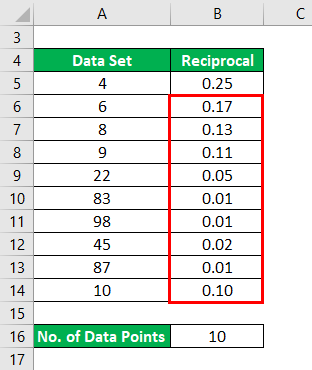
Similarly, We have to calculate Reciprocal for all the data points.
Now, the Mean of Reciprocal is calculated as
- Mean of Reciprocal = (0.25+0.17+0.13+0.11+0.05+0.01+0.01+0.02+0.01+0.10) / 10
- Mean of Reciprocal = 0.85/ 10
- Mean of Reciprocal = 0.085
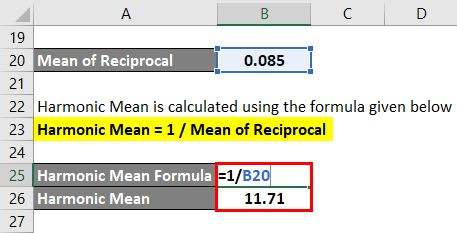
Harmonic Mean is calculated using the formula given below
Harmonic Mean = n / (1/X1 + 1/X2 + 1/X3 ………… 1/Xn)
Harmonic Mean = 1 / Mean of Reciprocal
- Harmonic Mean = 1/0.085
- Harmonic Mean = 11.71
Harmonic Mean Formula – Example #2
Now let see some other examples from practical life to understand mean more clearly and see the difference between arithmetic and harmonic mean.
Let say you are driving a car and traveling to some other town. The total time for your journey is 4 hours, out of which you drive at the speed of 60 km/hour during the 1st hour, 50 km/hour during 2nd hour, 100 km/hour during the 3rd hour and 40 km/hour during the 4th hour.
So your average speed can be calculated by simple mean:
- Average Speed = (60 + 50 + 100 + 40) / 4
- Average Speed = 250 / 4
- Average Speed = 62.5 km/hour
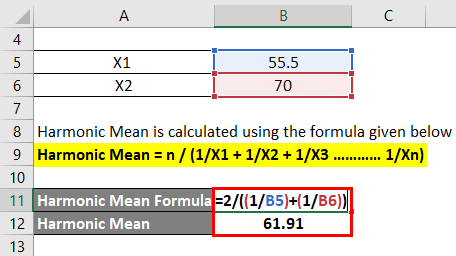
But let’s say the information given is that for the first half of the time, you drove at a speed of 55.5 km/hour and the next half at the speed of 70 km/hour. In that case, we need to use a harmonic mean to find the average speed.
Harmonic Mean is calculated using the formula given below
Harmonic Mean = n / (1/X1 + 1/X2 + 1/X3 ………… 1/Xn)
- Harmonic Mean = 2 / ((1/55.5) + (1/70))
- Harmonic Mean = 61.91 km/hour
If you see here, the value of the harmonic mean is less than the simple average.
Explanation
Although the harmonic mean is basically used to find the average of the data set, like simple arithmetic mean, it is not calculated as simply an arithmetic mean. If we have a large data set, the calculation of harmonic mean will become complex and time-consuming. With complexity comes confusion and chances of error. So one needs to be very careful while calculating the harmonic mean of a large data set. Since we take reciprocal in a calculation of harmonic mean, the highest weight is given to the lowest value and vice versa. Sometimes this is not required.
Another drawback is that if any of the data points in the data set is 0, the harmonic mean cannot be calculated since x/0 is not defined. So in a way, harmonic mean has very limited scope, unlike an arithmetic mean. Also, this is extremely sensitive toward outliers and extreme values.
Relevance and Uses of Harmonic Mean Formula
We have seen multiple limitations of harmonic mean, and that is the reason that it does not have much practical application. But there are some uses and positive points also. The harmonic mean is rigidly defined and because of which it is suitable for further mathematical operations. Also, unlike the geometric mean, it is not affected by sampling fluctuations. Since it gives greater weights to small data sets, which is sometimes desirable so that data is not biased towards high values. In situations that involve time and rates, a harmonic mean gives better and precise results than a simple mean.
All said and done, harmonic mean has few advantages, but since it has limited scope and its disadvantages are more, it is not used very often and has a limited presence.
Harmonic Mean Formula Calculator
You can use the following Harmonic Mean Calculator
| n | |
| X1 | |
| X2 | |
| X3 | |
| Harmonic Mean Formula | |
| Harmonic Mean Formula = |
|
|
Recommended Articles
This has been a guide to Harmonic Mean Formula. Here we discuss how to calculate Harmonic Mean along with practical examples. We also provide a Harmonic Mean calculator with a downloadable excel template. You may also look at the following articles to learn more –