Updated July 27, 2023

Hypergeometric Distribution Formula (Table of Contents)
What is Hypergeometric Distribution Formula?
The hypergeometric distribution is a discrete probability distribution in statistics. It is very similar to binomial distribution, and we can say with confidence that binomial distribution is a great approximation for hypergeometric distribution only if 5% or less of the population is sampled.
If we have random draws, hypergeometric distribution is a probability of success without replacing the item once drawn. But in a binomial distribution, the probability is calculated with replacement. For example, You have a basket with N balls, out of which “n” are black, and you draw “m” balls without replacing any of the balls. So hypergeometric distribution is the probability distribution of the number of black balls drawn from the basket.
Formula For Hypergeometric Distribution:
Where,
- K – Number of “successes” in Population
- k – Number of “successes” in the sample
- N – Population size
- n – Sample Size
To understand the hypergeometric distribution formula, one should be well aware of the binomial distribution and the Combination formula.
Combination Formula:
C(n,r) = n! / (r! * (n-r)!)
- n! – n factorial = n*(n-1)*(n-2)………..*1
- r! – r factorial = r*(r-1)*(r-2)………..*1
- (n-r)! – (n-r) factorial = (n-r)*(n-r-1)*(n-r-2)………..*1
Examples of Hypergeometric Distribution Formula (With Excel Template)
Let’s take an example to understand the calculation of the Hypergeometric Distribution in a better manner.
Hypergeometric Distribution Formula – Example #1
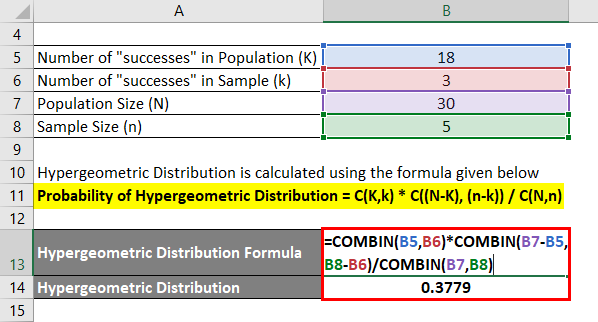
Let’s Say you have a deck of colored cards with 30 cards, out of which 12 are black and 18 are yellow. You have drawn 5 cards randomly without replacing any of the cards. Now you want to find the probability of exactly 3 yellow cards being drawn.
Solution:
The formula to calculate Hypergeometric Distribution is as below:
Probability of Hypergeometric Distribution = C(K,k) * C((N – K), (n – k)) / C(N,n)
- Probability of getting exactly 3 yellow cards = C(18,3) * C((30-18), (5-3)) / C(30,5)
- Probability of getting exactly 3 yellow cards = C(18,3) * C(12, 2) / C(30,5)
- Probability of getting exactly 3 yellow cards = (18! / (3! * 15!) ) * (12! / (2! *10!) ) / (30! / (5! *25!) )
- Probability of getting exactly 3 yellow cards = 0.3779
Hypergeometric Distribution Formula – Example #2
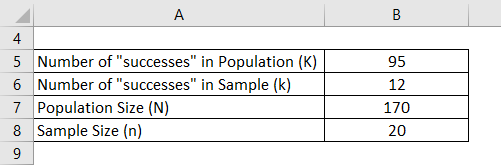
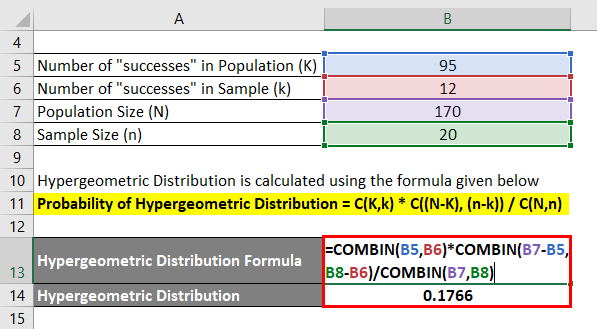
Let’s say you live in a very small town with 75 females and 95 males. Now there was voting in your town, and everyone voted. A sample of 20 voters was selected randomly. You want to calculate what is the probability that exactly 12 of these voters were male voters.
Solution:
The formula to calculate Hypergeometric Distribution is as below:
Probability of Hypergeometric Distribution = C(K,k) * C((N – K), (n – k)) / C(N,n)
- Probability of getting 12 male voters = C(95,12) * C((170-95), (20-12)) / C(170,20)
- Probability of getting 12 male voters = C(95,12) * C(75, 8) / C(170,20)
- Probability of getting 12 male voters = (95! / (12! * 83!) ) * (75! / (8! *63!) ) / (170! / (20! *150!) )
- Probability of getting 12 male voters = 0.1766
Explanation
The hypergeometric distribution requires meeting several criteria to perform this type of experiment or distribution, which is similar to a binomial distribution but does not allow replacement.
- The first and foremost requirement is that the data collected should be discrete in nature.
- Each pick or draw should not be replaced by another because whenever a random variable is drawn without replacement, it is not independent and relates to what was drawn earlier.
- There must be 2 sets of different groups, and you want to know the probability of a specific number of members of one group. For example, in the voting example, we have males and females. In the bag example, we have a yellow and black group.
Along with these assumptions, combination knowledge also plays a vital role in performing hypergeometric distribution. So it is imperative that one should know the concepts of combination before proceeding to hypergeometric distribution.
Relevance and Uses of Hypergeometric Distribution Formula
Hypergeometric distribution has many uses in statistics and practical life. The most common use of the hypergeometric distribution, which we have seen above in the examples, is calculating the probability of samples drawn from a set without replacement. In real life, the best example is the lottery. So in a lottery, once the number is out, it cannot go back and can be replaced, so hypergeometric distribution is perfect for this type of situation.
Recommended Articles
This is a guide to Hypergeometric Distribution Formula. Here we discuss How to Calculate Hypergeometric Distribution along with practical examples. We also provide a downloadable Excel template. You may also look at the following articles to learn more –