Updated March 30, 2023
Definition of Insertion Sort Algorithm
Insertion sort is one of the algorithms used for sorting the element in an array; it is simple and easy to understand. This sorting algorithm divided the array into two parts sorted and unsorted array. After that, we compare each element with the previous one; if the element is smaller than the previous element, we just swap them and keep comparing the element. So basically, we pick up the values from the unsorted array, but it exists only virtually and place them into the correct place in the array by comparing it with the previous element; in the coming section of the tutorial, we will have the internal working of the Insertion sort algorithm in details for better understanding and implement this to sort the given array.
Insertion Sort Algorithm
As we have already discussed, it is one of the sorting algorithms, which is used to sort the elements of the array; we can write the logic in any programming language for this, but first, let’s take a look at the steps we need to take in order to implement this algorithm for our usage in the program see below;
Algorithm:
- It first picks up the first element and considers it to be already sorted, so it simply returns 1 in this case.
- Now in this step, it will pick up the next element to be sorted.
- It will now compare these current picked-up elements with all the elements in the sorted sub-list.
- If the picked up element is smaller than the element to be sorted, then it will just shift all the elements of the array
- Now it will insert the value at the correct place in the array
- basic, flow for the insertion sort.
- Repeat the above process until the list or array is sorted.
As you can see, we have to follow the above steps in order to write our logic in any programming language, but for this tutorial, we will consider it to be in Java for beginners.
How Insertion Algorithm Works?
As in the tutorial, we have already seen the algorithm steps that we need to follow in order to sort our list or array by using an insertion algorithm, but in this section, we will mainly focus on the internal working of this algorithm in detail, by taking one simple input array or a list object in order to get the better idea how it works internally, and how it picks the element from the array to sort them. This will give us a clearer idea about the insertion algorithm and make it even easier for us to write our logic accordingly. Also, in the later part, we will take a look at the complexity for this algorithm in detail. Let’s get started;
1. Input Array :
Ex:
14, 33, 27, 10, 35, 19, 42, 44
2. We have the above input array, and we will now pick up the first elements from the array, as sorted that is ’14’.
3. Now, we will compare the first two elements from the array, but it is already sorted in our case because 14 is lesser than 33 here.
4. Now, we will go over the pointer to the next two elements that are 33 and 27; now, in this case, 33 is greater than 27, so we will place 27 at the place of 33 like below;
Ex:
14, 27, 33, 10, 35, 19, 42, 44
5. Now, we will compare the sorted sun list element now; we have 27 and 14, but they are already in sorted order so that we will move ahead.
6. Now, the next two-element we have is 33 and 10; 33 is greater than 10, so we will swap i and place 10 at 33.
Ex:
14, 27, 10, 33, 35, 19, 42, 44
But here again, 10 is smaller than 27, so we will keep on searching and swapping the elements from the sorted sub-list we have. So at the end, we will get something like the below;
Ex:
10, 14, 27, 33, 35, 19, 42, 44
7. Now, we will move with the next two elements that is 33 and 35, but they are in sorted order already, so we will move to the next elements that is 35 and 19, and we have to repeat the same process as above until the sorted sub list is in the correct order.
So all these steps will keep on doing until we get the sorted list from it. In the end, we will get output as below;
Ex:
10, 14, 19, 27, 33, 35, 42, 44
Let’s take a look at the correct for this algorithm, see below;
This algorithm has the time and auxiliary complexity as below;
- a) auxiliary complexity :o(1)
- b) time complexity : o(n^2)
Example of Insertion Sort Algorithm
Different examples are mentioned below:
- java program for insertion sort.
Example:
package com;
class InsertionSortDemo {
void insertionsortLogic(int myarray[])
{
int n = myarray.length;
for (int i = 1; i < n; ++i) {
int pointer = myarray[i];
int j = i - 1;
while (j >= 0 && myarray[j] > pointer) {
myarray[j + 1] = myarray[j];
j = j - 1;
}
myarray[j + 1] = pointer;
}
}
static void printSortedArray(int myarray[])
{
int n = myarray.length;
for (int i = 0; i < n; ++i){
System.out.print(myarray[i] + " ");
}
System.out.println("*******************************************");
}
public static void main(String args[])
{
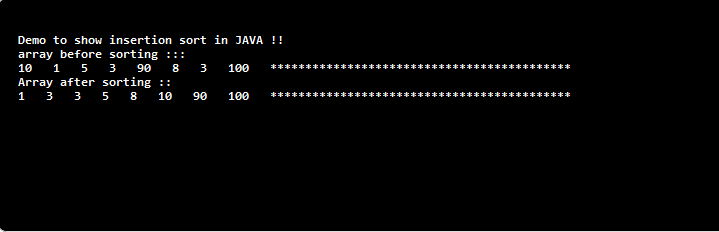
System.out.println("Demo to show insertion sort in JAVA !!");
int array[] = { 10, 1, 5, 3, 90, 8, 3, 100};
System.out.println("array before sorting :::");
printSortedArray(array);
InsertionSortDemo ob = new InsertionSortDemo();
ob.insertionsortLogic(array);
System.out.println("Array after sorting :: ");
printSortedArray(array);
}
}
Output:
Conclusion
Using this sorting algorithm, we can easily sort the array; as we have already seen, it is easy and simple with very much less overhead and understood by the developers, so just follow the steps and write the logic for it to sort the list. Also, we have seen the complexity for this algorithm to be considered while making it a choice for sorting our list or array object.
Recommended Articles
This is a guide to Insertion Sort Algorithm. Here we also discuss the definition and how insertion algorithm works? Along with example. You may also have a look at the following articles to learn more –