Updated December 30, 2023
Introduction
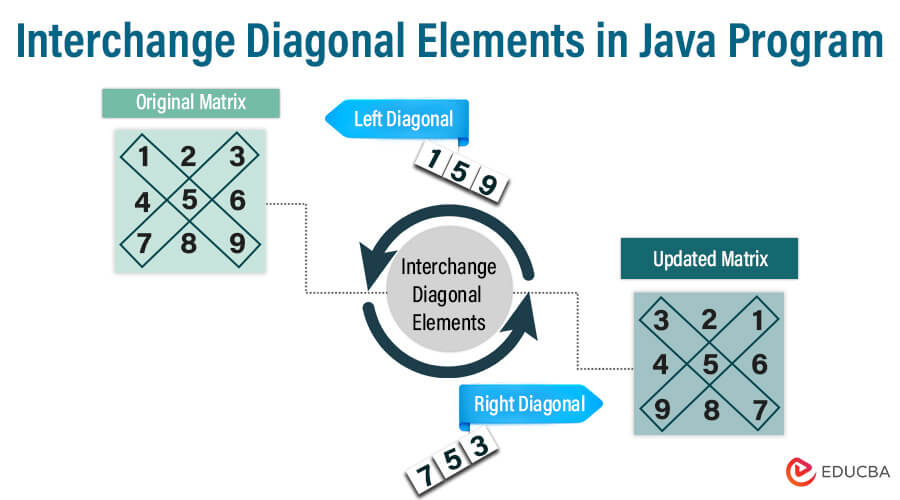
Interchanging diagonal elements in a Java program is a common operation performed on two-dimensional arrays, specifically matrices. This operation involves swapping the elements located on the primary diagonal with those on the secondary diagonal of a square matrix. In a square matrix, the primary diagonal is the diagonal that stretches from the top-left corner to the bottom-right corner. In contrast, the secondary diagonal extends from the top-right corner to the bottom-left corner. We have created simple examples and use cases to help you work around diagonal elements within an array.
Let us understand a Simple Example:
A(i, i) where i = a,b,c,d.
[a b] After Interchange the Diagonal [b a]
[c d] [d c]
Table of Contents
- Introduction to Interchange Diagonal Elements in Java Program
- Understanding Diagonal Elements
- What is a Matrix in Java?
- Why do we need to interchange?
- Algorithm
- Java Program Structure
- Time Complexity
Key Takeaways
- Diagonal elements in a matrix have the same row index and column index. For example- (0,0), (1,1), (2,2), and so on.
- To interchange diagonal elements, we can use different methods.
- Interchanging diagonal elements can help in complex computations.
Understanding Diagonal Elements
In a matrix, diagonal elements fall on the main diagonal. The main diagonal entries in a square matrix represent from the top-left corner to the bottom-right corner. These elements have the same row and column index. In other words, if a matrix is denoted by n×n, the diagonal elements are A(i, i), where i= 1,2,3, and so on.
For example:
1 2 3
4 5 6
7 8 9
In the above matrix, 1,5 and 9 are the correct diagonal elements.
And 3,5, and 7 are the left diagonal elements.
After the interchange, the matrix will be.
3 2 1
4 5 6
9 8 7
What is a Matrix in Java?
A matrix is a rectangular array with elements arranged in rows and columns. To access an element within a matrix at row “r” and column “c,” use index “array[r][c].” You will get the value of that particular element.
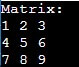
Below is a simple example of a 2×3 matrix.
Code:
public class MatrixExample {
public static void main(String[] args) {
// Define a 2x3 matrix
int[][] matrix = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
// Print the matrix
System.out.println("Matrix:");
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}Output:
Why do we need to interchange?
There could be several reasons for interchanging the diagonal elements of a matrix, and we have mentioned some of them here.
- To maintain the symmetry of the matrix.
- It is helpful as a part of transposing the matrix.
- To maintain a specific order of the diagonal elements for further computations.
- To change the visual representation of the matrix as required for specific situations.
Algorithm
An algorithm must perform the following steps for the diagonal interchanging operation.
- First, declare variables to define the size of the matrix.
- Initialize the rows’ elements and columns’ elements for that matrix.
- Confirm if rows “R” and columns “C” are the same in number.
- If R=C, then ask the user to initialize the matrix.
- Command to display the given matrix.
- Now, interchange the diagonal of the given matrix.
- Now, print the matrix with interchanged diagonal elements.
- If R is not equal to C, then print the message.
Java Program Structure
Example #1
Now that you have understood the logic, let’s look at the example below of a 3×3 matrix.
Code:
import java.util.Scanner;
public class InterchangeDiagonalDemo
{
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
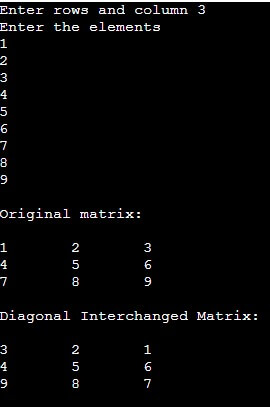
System.out.print("Enter rows and column");
int n=sc.nextInt();
int a[][] = new int [n][n];
//input matrix elements
System.out.println("Enter the elements");
//loop for rows
for(int i=0; i<n; i++)
{
//loop for column
for(int j=0; j<n; j++)
{
//reading matrix elements
a[i][j]=sc.nextInt();
}
}
//print the original matrix
System.out.println("\nOriginal matrix: \n");
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
System.out.print(a[i][j]+"\t");
}
System.out.println(" ");
}
//swapping elements
for(int i=0; i<n; i++)
{
int temp = a[i][i];
a[i][i] = a[i][n-i-1];
a[i][n-i-1] = temp;
}
//prints the diagonal interchanged matrix
System.out.println("\nDiagonal Interchanged Matrix: \n");
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
System.out.print(a[i][j]+"\t");
}
System.out.println(" ");
}
}
}Output:
Example #2
The example below will encapsulate the interchange process into functions implementing object-oriented programming.
Code:
public class InterchangeDiag {
public static int matrix_sizes = 3;
static void interchange_diag(int input_matrix[][]) {
for (int i = 0; i < matrix_sizes; ++i)
if (i != matrix_size / 2) {
int temp = input_matrix[i][i];
input_matrix[i][i] = input_matrix[i][matrix_size - i - 1];
input_matrix[i][matrix_size - i - 1] = temp;
}
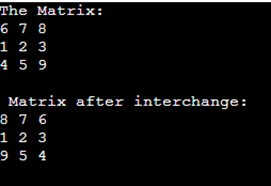
System.out.println("\n Matrix after interchange: ");
for (int i = 0; i < matrix_sizes; ++i) {
for (int j = 0; j < matrix_size; ++j)
System.out.print(input_matrix[i][j]+" ");
System.out.println();
}
}
public static void main (String[] args) {
int input_matrix[][] = {
{6, 7, 8},
{1, 2, 3},
{4, 5, 9}
};
System.out.println("The Matrix: ");
for (int i = 0; i < matrix_sizes; i++) {
for (int j = 0; j < matrix_size; j++) {
System.out.print(input_matrix[i][j] + " ");
}
System.out.println();
}
interchange_diag(input_matrix);
}
}Output:
Example #3
The example below will be Using XOR to encapsulate the operations into functions implementing object-oriented programming.
Code:
public class DiagonalInterchange {
public static void main(String[] args) {
int[][] matrix = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
System.out.println("Original Matrix:");
printMatrix(matrix);
interchangeDiagonal(matrix);
System.out.println("Matrix after interchanging diagonal elements:");
printMatrix(matrix);
}
private static void interchangeDiagonal(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n; i++) {
// XOR swap for diagonal elements
matrix[i][i] = matrix[i][i] ^ matrix[n - 1 - i][n - 1 - i];
matrix[n - 1 - i][n - 1 - i] = matrix[i][i] ^ matrix[n - 1 - i][n - 1 - i];
matrix[i][i] = matrix[i][i] ^ matrix[n - 1 - i][n - 1 - i];
}
}
private static void printMatrix(int[][] matrix) {
for (int[] row : matrix) {
for (int element : row) {
System.out.print(element + " ");
}
System.out.println();
}
System.out.println();
}
}Output:
Time Complexity
We will explain the time complexity in terms of the above example, making it more accessible for you to understand. The time complexity is constant or O(1) because the number of operations remains the same regardless of the input size (in this case, the matrix size).
In the above example, we interchanged two elements, precisely the elements at positions (0,0) and (1,1). This operation involves a fixed number of steps that do not increase with the size of the input matrix. So, whether it is a 2×2 matrix or a larger matrix, the number of operations for swapping diagonal elements remains constant.
Conclusion
In Java, you can perform different operations on a matrix and its elements to ease many complex computations. One of the commonly used is interchanging the diagonal elements. You can follow specific steps to interchange the elements, with the time complexity remaining the same for every matrix size.
FAQs
Q1. What is the first condition to perform a diagonal interchange operation?
Answer: You must check if the given matrix has the same number of columns and rows. Otherwise, you will get an error.
Q2. Does interchanging diagonal elements affect matrix properties?
Answer: Yes, interchanging diagonal elements may impact the properties of the matrix, especially if it involves creating or breaking symmetry.
Q3. What is the space complexity of interchanging diagonal elements?
Answer: The space complexity is O(1) as the process does not involve extra space in allocating the memory.
Recommended Articles
We hope this EDUCBA information on “Interchange Diagonal Elements in Java Program” benefited you. You can view EDUCBA’s recommended articles for more information.