Knapsack Problem Python

Solving the Knapsack Problem

There are three ways to solve a knapsack problem using python programming.

• Greedy Method
• Dynamic Programming
• Brute Force

1. Greedy Method

Code:

class KnapsackPackage(object):        
    """ Knapsack Package Data Class """
    def __init__(self, weight, value): 
        self.weight = weight 
        self.value = value 
        self.cost = value / weight 
    def __lt__(self, other): 
        return self.cost < other.cost
if __name__ == "__main__": 
    W = [15, 10, 2, 4] 
    V = [30, 25, 2, 6] 
    M = 37
    n = 4     
    proc = FractionalKnapsack()
    proc.knapsackGreProc(W, V, M, n)
class FractionalKnapsack(object):
    def __init__(self):
        def knapsackGreProc(self, W, V, M, n):
            packs = []
        for i in range(n): 
            packs.append(KnapsackPackage(W[i], V[i]))
            packs.sort(reverse = True)         
        remain = M
        result = 0         
        i = 0
        stopProc = False
        while (stopProc != True):
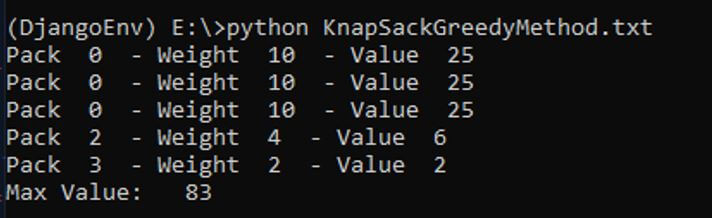
            if (packs[i].weight <= remain): remain -= packs[i].weight; result += packs[i].value; print("Pack ", i, " - Weight ", packs[i].weight, " - Value ", packs[i].value) if (packs[i].weight > remain):
                i += 1
                 
            if (i == n):
                stopProc = True           
                print("Max Value:\t", result)

Output:

Explanation:

• The Greedy algorithm’s idea is to calculate the ratio of value and weight then choose the ratios by sorting them in descending order. The first ratio is the maximum package number, so choose the first ratio.
• You need to fill the knapsack until remain is greater than the weight when it crosses the weight the loop should break and display the output value.

2. Dynamic Programming

Code:

def knapSack(W, wt, val, n): 
    K = [[0 for x in range(W + 1)] for x in range(n + 1)]    
    # Build table K[][] in bottom to up manner 
    for i in range(n + 1): 
        for w in range(W + 1): 
            if (i == 0 or w == 0): 
                K[i][w] = 0
            elif wt[i-1] <= w: 
                K[i][w] = max(val[i-1] 
                          + K[i-1][w-wt[i-1]],   
                              K[i-1][w]) 
            else: 
                K[i][w] = K[i-1][w]    
    return K[n][W]    
# Driver code 
val = [60, 100, 120] 
wt = [10, 20, 30] 
W = 50
n = len(val) 
print(knapSack(W, wt, val, n)) 

Output:

Explanation:

• In Dynamic Programming, the given problem is divided into subproblems.
• The subproblems are again divided into many subproblems. They get divided until you get subproblems that can be easily solved.

3. Brute Force

Code:

def knapSack(W, wt, val, n):
   # initial conditions
   if n == 0 or W == 0 :
      return 0
   # If weight is higher than capacity then it is not included
   if (wt[n-1] > W):
      return knapSack(W, wt, val, n-1)
   # return either nth item being included or not
   else:
      return max(val[n-1] + knapSack(W-wt[n-1], wt, val, n-1),
         knapSack(W, wt, val, n-1))
# To test above function
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
print (knapSack(W, wt, val, n))

Output:

Explanation:

• Brute Force solves the problem by checking if there are ‘n’ items from which you have to choose, then there is a possibility to get 2n combinations of elements in the Knapsack. Whether the item is either chosen or not, a bit-string of 0’s and 1’s is obtained, whose length will be equal to the number of items.
• If the ‘i’th symbol of that string is 0, then consider that the item is not chosen. And if the ‘i’th symbol of that string is 1, consider the item as chosen.

Conclusion

In this article, we have discussed the approaches to solve a Knapsack problem. n items are given along with the weights and values of it. The task is to choose the set of weights that fill the maximum capacity of the bag by fulfilling all the given conditions. The first step of the programmer is to set each item’s number so that it includes in the collection and finally to check whether the total weight is less than or equal to a specific limit. The Greedy algorithm’s idea is to calculate the ratio of value and weight then choose the ratios by sorting them in descending order. In Dynamic Programming, the given problem is divided into subproblems. Brute force is the best approach to solve any Knapsack problem. If there are ‘n’ items from which you have to choose, then there is a possibility to get 2n combinations of elements in the Knapsack. By using the combinations the problem is solved.

Recommended Articles

We hope that this EDUCBA information on “Knapsack Problem Python” was beneficial to you. You can view EDUCBA’s recommended articles for more information.

1.  BFS Algorithm Python
2. Tree Traversal Python
3. DFS Algorithm in Python
4. Linked List in Python