Updated July 25, 2023
Marginal Benefit Formula (Table of Contents)
What is the Marginal Benefit Formula?
The term “marginal benefit” refers to the incremental benefit enjoyed by a consumer on the consumption of one additional unit of a good or service.
In other words, a consumer will be willing to pay more for something which gives him a greater sense of satisfaction or he thinks is more beneficial to him, and marginal benefit helps you in measuring those different level of satisfaction for each unit of a good or service.
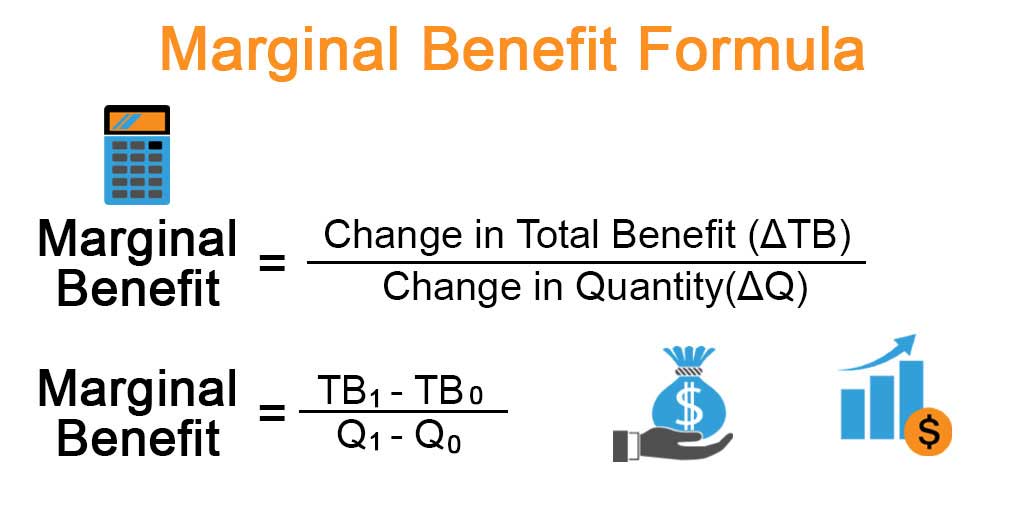
The formula for the marginal benefit can be derived by dividing the change in total benefit (ΔTB) by the change in the quantity of the good or service (ΔQ). Mathematically, it is represented as,
The formula for the marginal benefit can also be computed as,
where,
- TB0 = Initial Total Benefit at Quantity Q0
- TB1 = Final Total Benefit at Quantity Q1
- Q0 = Initial Quantity
- Q1 = Final Quantity
Examples of Marginal Benefit Formula (With Excel Template)
Let’s take an example to understand the calculation of Marginal Benefit in a better manner.
Marginal Benefit Formula – Example #1
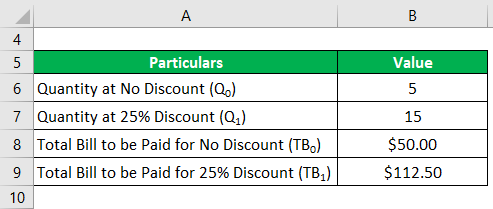
Let us take a simple example where a consumer is willing to pay $10 each for the first five chocolates. However, he wants to buy another set of ten chocolates but not for more than $5 each. Do you think the consumer will buy the next set of chocolates if the seller offers him a 25% discount on the purchase of all the 15 chocolates?
Solution:
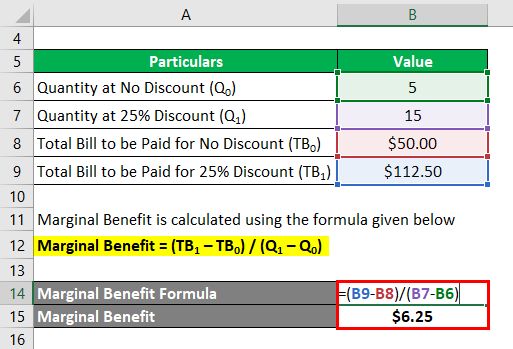
Marginal Benefit is calculated using the formula given below
Marginal Benefit = (TB1 – TB0) / (Q1 – Q0)
- Marginal Benefit = ($112.50 – $50.00) / (15 – 5)
- Marginal Benefit = $6.25 per chocolate
Since the next set of chocolates are priced higher ($6.25) than what the consumer in willing to pay ($5), he will not buy the next 10 chocolates.
Marginal Benefit Formula – Example #2
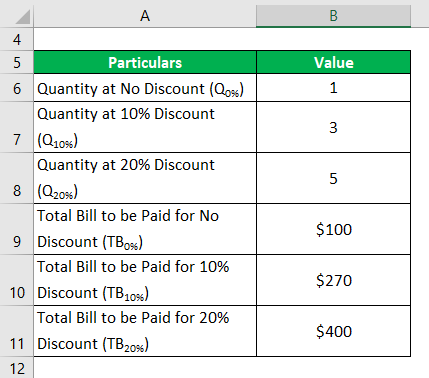
Let us take the example of a consumer who recently went to a mall to buy himself a few T-shirts. There he came across a stall that was offering each T-shirt for $100. However, there were few offers that said, “if you buy 3 T-shirts then 10% discount, 5 T-shirts then 20% discount”. The discount was on the overall purchase value. Calculate the marginal benefit for the consumer in each of the offers based on the given information.
Solution:
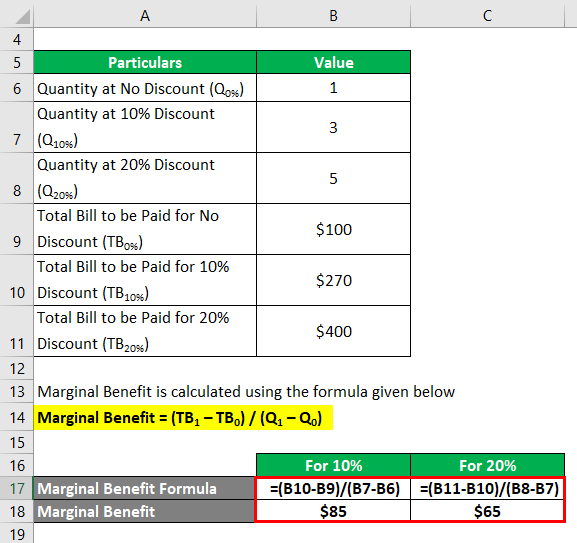
Marginal Benefit is calculated using the formula given below
Marginal Benefit = (TB1 – TB0) / (Q1 – Q0)
Consumer at 10% Discount
Marginal Benefit = (TB10% – TB0%) / (Q10% – Q0%)
- Marginal Benefit = ($270 – $100) / (3 – 1)
- Marginal Benefit = $85 per T-shirt
Consumer at 20% Discount
Marginal Benefit = (TB20% – TB10%) / (Q20% – Q10%)
- Marginal Benefit = ($400 – $270) / (5 – 3)
- Marginal Benefit = $65 per T-shirt
Therefore, it can be seen that the consumer’s perceived benefit is expected to decline from $100 per shirt to $65 per T-shirt with an increase in the purchase of T-shirts. This is the phenomenon of marginal benefit.
Explanation
The formula for the marginal benefit can be computed by using the following steps:
Step 1: Firstly, determine the initial quantity of the good or service consumed and the total benefit that the consumer finds in that. The total money that a consumer is willing to pay can be used as a proxy for total benefit. The initial quantity and initial total benefit are denoted by Q0 and TB0 respectively.
Step 2: Next, determine the final quantity of the goods or service consumed and the total money that the consumer is willing to pay for that quantity and they are denoted by Q1 and TB1 respectively.
Step 3: Next, compute the change in the total benefit which is the final total benefit (step 2) minus initial total benefit (step 1).
Change in Total Benefit (ΔTB) = TB1 – TB0
Step 4: Next, compute the change in the quantity of the good or service consumed which is the final quantity (step 2) minus initial quantity (step 1).
Change in Quantity (ΔQ) = Q1 – Q0
Step 5: Finally, the formula for the marginal benefit can be derived by dividing the change in total benefit (step 3) by the change in quantity (step 4) as shown below.
Marginal Benefit = Change in Total Benefit (ΔTB) / Change in Quantity (ΔQ)
Marginal Benefit = (TB1 – TB0) / (Q1 – Q0)
Relevance and Use of Marginal Benefit Formula
The concept of marginal benefit is also based on the theory of marginal utility or the law of diminishing marginal returns. As such, a consumer usually experiences the highest marginal benefit only on the consumption of the first unit, after which it eventually starts to decline.
It is important to understand the concept from the point of view of a seller because this sense of perceived benefit of the consumer can be used to maneuver discount offers. As such, this concept is used in many business applications, which primarily revolves around marketing and pricing strategies.
Marginal Benefit Formula Calculator
You can use the following Marginal Benefit Formula Calculator
| TB1 | |
| TB0 | |
| Q1 | |
| Q0 | |
| Marginal Benefit | |
| Marginal Benefit = |
|
|
Recommended Articles
This is a guide to Marginal Benefit Formula. Here we discuss how to calculate Marginal Benefit Formula along with practical examples. We also provide a Marginal Benefit calculator with a downloadable excel template. You may also look at the following articles to learn more –