Introduction to MATLAB Exponential Function
MATLAB has a variety of commands & functions with numerous utilities. This article will focus on understanding a very important MATLAB function called the ‘exponential function’. We use exp(x) to calculate the exponential of a function passed as an argument. We will also understand how we can visually represent the exponential function. The function whose exponential we wish to calculate, is passed as an argument to the ‘exp’ command.
Let’s first refresh our understanding of the exponential function.
Exponential function is a function where the constant is ‘e’ and it is raised to the power of an argument.
It can be represented as f(x) = b(x)
Here ‘b’ represents a real number which is positive
X represent an exponent argument
Exponential functions are functions of a real variable and the growth rate of these functions is directly proportional to the value of the function. The growth rate is actually the derivative of the function.
In the exponential function, the exponent is an independent variable.
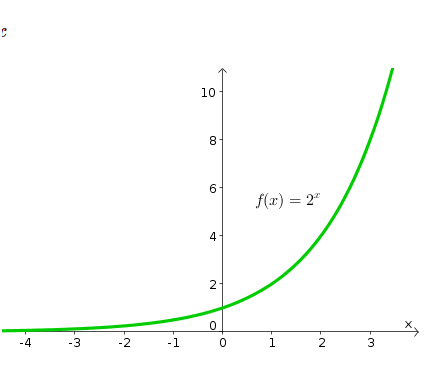
Following is a simple example of the exponential function:
F(x) = 2 ^ x
As depicted in the above graph, the exponential function increases rapidly. Let’s take another function:
g(x) =1/2 raised to the power x, which is an example of exponential decay, the function decreases rapidly as x increases.
For f(x) in the previous example, the function doubles every time we add to x. In the exponential decay of the function, the function decreases to half every time we add to x. This is a feature of exponential functions, indicating how fast they grow or decay.
Example of MATLAB Exponential Function
Below are the examples of MATLAB Exponential:
Now we have brushed our understanding of exponential function, let’s understand its use in MATLAB.
Syntax:
exp (X)
y = exp (X) will return the exponential function ‘e’ raised to the power ‘x’ for every element in the array X.
It can also be used for complex elements of the form z = x + iy.
The output will be
e ^ z = e ^ x (sin y + i cos y)
Now we will understand the above syntax with the help of various examples
Types of Exponential Function in MATLAB
Below are the types of the exponential function in Matlab:
1. Exponential of unity
Let’s first compute the exponential of unity (1).
Code:
exp (1)
Output:
2. Exponential of Positive Number
Let us now take exponential of another positive number.
Code:
exp (3)
Output:
3. Exponential of Negative Numbers
The exponential of negative numbers is also possible. For our understanding let’s take the exponential of ‘-3’.
Code:
exp (-3)
Output:
4. Exponential of Fractions
In the above examples, we saw how to take exponential of integers, we can also take exponential of fractions. For our understanding, let’s take fraction ¼ as an example.
Code:
exp (1 / 4)
Output:
5. Exponential of Floating Point Values
We can also calculate the exponential of floating point numbers. Let’s take a floating point value 2.23 for our understanding.
Code:
exp (2.23)
Output:
6. Exponential of Logarithmic Function
We can also calculate the exponential of a logarithmic function. Let’s take value ‘-2’ for our understanding.
Code:
exp (log (-2))
Output:
7. Plotting an Exponential Function
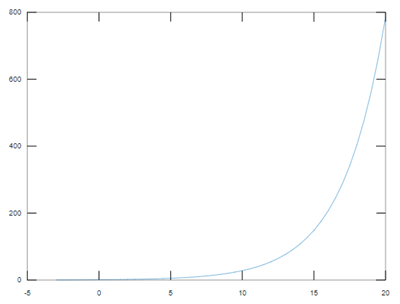
Let us now learn how can we plot an exponential function. A plot is visually more powerful than normal data when we want to analyze the behavior of our function.
Example:
Our function is A = e ^ (x / 3)
Let’s assume the values to be in the range [-3, 20]. This is how our input will look like:
Code:
X = -3 : 0.5 : 20;
A = exp (X / 3);
plot (X, A)
Output:
So, in this article, we learned how to use the exponential function in MATLAB. We can use exp(x) syntax in MATLAB to calculate the exponential of any function which is passed as an argument. We can also plot the functions which we have computed using the ‘plot’ expression, which allows us to visually interpret our function.
Recommended Articles
This is a guide to MATLAB Exponential. Here we discuss the Introduction to MATLAB Exponential and its different Examples as well as its input and output. You can also go through our suggested articles to learn more –