Updated March 13, 2023

Introduction to Matlab linear regression
Matlab provides the functionality to implement the linear regression; basically, data models are used to determine the relationship between the response and predictor variables. So linear regression is useful in data models, and it acts as a model coefficient. There are multiple types of linear regression, but the most common is least squares, and it is suitable for both the lines and polynomials as well as other types of linear regression. Before finding the relationship between the response and predictor, it is necessary to analyze the linear relationship between them. That means if there is an existing relationship between them, then we need to analyze first after that to calculate the model coefficient.
Syntax
ployfit(A, B, N)
Explanation
By using the above syntax, we can find the linear coefficient for the given equation, here we have A and B for the data set, and the N is the degree of the equation. Normally this syntax is suitable for data analysis.
Now let’s see the syntax for the graphics command as follows.
plot(A, B, S)
Explanation
In the above syntax, we specify the three parameters such as A and B for the data point and S for the symbol. In this syntax, it automatically creates the popup window, and that window shows the data point that is (A and B). This data point is used to specify the linear regression with the symbol and color. So in this way, we can execute the multiple graphics command as per our requirement.
How linear regression works in Matlab?
Now let’s see how linear regression works in Matlab as follows.
We need to follow the several steps to generate the linear regression in Matlab as follows.
1. The first step we need to prepare the data
We need to put our data into a format that fitting to the regression; also, we need to put data that acceptable in a specified function. Input data is placed in an array X, and response data is placed in a separate vector that we call y, or input data is placed in a table or dataset array atable, and response data is placed as a column in atablel. One observation is represented by each row of the input data. Each column corresponds to a single prediction (variable).
For example table or dataset of the array that is atable that indicates the response variable name with value pair.
LR= fitlm(atable, response ‘variable name’, ‘value’);
2. In the second step we need to select the fitting method
Basically, there are three different ways to fit the model as follows.
- Least-Squares Fit
Fitlm is a tool for creating the least-squares fit of a model to data. This strategy works well when you have a good idea of the model’s shape and just need to figure out its parameters. When you want to look at a few different models, this strategy is also handy.
- Robust Fit
Fitlm and the RobustOpts name-value pair can be used to generate a model that is affected by the outliers. Robust fitting eliminates the need to manually eliminate outliers. Step, on the other hand, does not operate with robust fitting. This means that when you employ robust fitting, you can’t look for a decent model step by step.
- Stepwise Fit
In this method, we need to find the data model and after that fit the parameters to the specified model. In this method, we use stepwiselm to start this method. By using this method we can find the best model that is relevant to our terms. When we start this method with constant then it leads to the small model and when we start this method with more than one term then it leads to the complex model.
-
In the third step we need to select the range of models
In Matlab, there are multiple ways to specify the model for the linear regression such as Brief Name, Terms Matrix, and formula.
-
Fit model to the specified data
In this step, we can fit the argument for the linear regression by using the fitlm and stepwiselm.
-
Examine the quality of the model
In this step, we examine the quality of the fitted model and as per the requirement, we can adjust the data model as well as we can display the model by using the mdl command.
Example of Matlab linear regression
Now let’s see the different examples of linear regression in Matlab for better understanding as follows.
Let’s see a simple example of linear regression as follows.
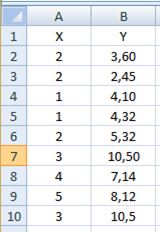
First, we need to create the excel file, here we created a linear.xlsx file and we inserted the following data as shown in the following screenshot as follows.
If we use online Simulink then we need to upload excel files and if we use offline mode then we need to create excel files on your specified location that you want. So here we use online mode so first, we need to upload the file.
After successfully uploading the file we need to import the excel file by using the import command that shows on the menu bar.
After importing the .xlsx file we need to execute the following command as follows.
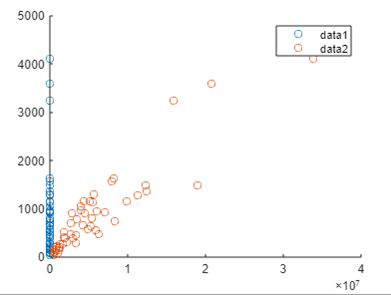
scatter(X,Y)
Explanation
After execution of the above command, we got a graph. The final output of the above statement we illustrated by using the following screenshot as follows.
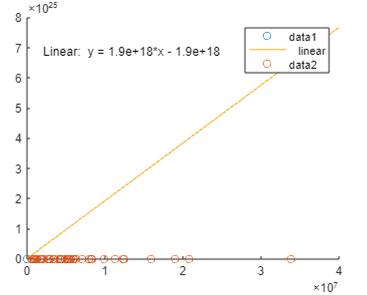
After that click on the tool menu and select the basic fitting option. In which we can select any option that we want, here we select the liner option and click on the show equation. The final output of the above linear equation we illustrated by using the following screenshot as follows.
So in this way, we can implement the basic linear regression equation as well as we can perform some mathematical calculations to solve the equation. At the same time, we can plot the graph for the specified linear equation as per requirement.
Conclusion
We hope from this article you learn Matlab linear regression. From the above article, we have learned the basic syntax of linear regression and we also see different examples of linear regression. From this article, we learned how and when we use Matlab linear regression.
Recommended Articles
This is a guide to Matlab linear regression. Here we discuss the basic syntax of linear regression and we also see different examples of linear regression. You may also have a look at the following articles to learn more –