Updated March 20, 2023

Overview of Matrix Multiplication in NumPy
Matrix Multiplication in NumPy is a python library used for scientific computing. Using this library, we can perform complex matrix operations like multiplication, dot product, multiplicative inverse, etc. in a single step. In this post, we will be learning about different types of matrix multiplication in the numpy library.
Different Types of Matrix Multiplication
There are primarily three different types of matrix multiplication :
| Function | Description |
| np.matmul(array a, array b) | Returns matrix product of two given arrays |
| np.multiply(array a, array b) | Returns element-wise multiplication of two given arrays |
| np.dot(array a, array b) | Returns scalar or dot product of two given arrays |
1. Matrix product of two given arrays
In order to find the matrix product of two given arrays, we can use the following function :
np.matmul(array a, array b)Input for this function cannot be a scalar value
| A = | all | a12 | a13 |
| a21 | a22 | a23 |
| B = | b11 | b12 | b13 |
| b21 | b22 | b23 | |
| b31 | b32 | b33 |
A @B =
| a11*b11 + a12*b21 + a13*b31 | a11*b12 + a12*b22 + a13*b32 | a11*b13 + a12*b23 + a13*b33 |
| a21*b11 + a22*b21 + a23*b31 | a21*b12 + a22*b22 + a23*b32 | a21*b13 + a22*b23 + a23*b33 |
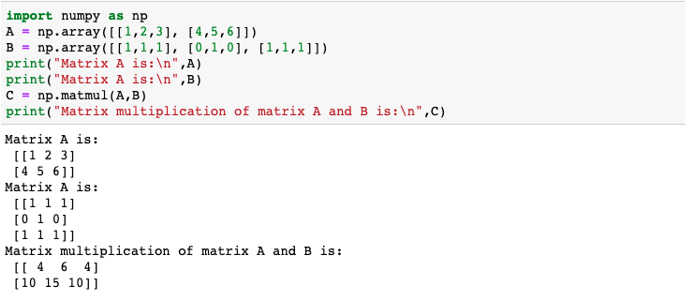
Example #1
Program to illustrate the matrix product of two given n-d arrays.
Code:
import numpy as np
A = np.array([[1,2,3], [4,5,6]])
B = np.array([[1,1,1], [0,1,0], [1,1,1]])
print("Matrix A is:\n",A)
print("Matrix A is:\n",B)
C = np.matmul(A,B)
print("Matrix multiplication of matrix A and B is:\n",C)The matrix product of the given arrays is calculated in the following ways:
| A= | 1 | 2 | 3 |
| 4 | 5 | 6 |
| B= | 1 | 1 | 1 |
| 0 | 1 | 0 | |
| 1 | 1 | 1 |
A @ B =
| 1*1 + 2*0 + 3*1 = 4 | 1*1 + 2*1 + 3*1 = 6 | 1*1 + 2*0 + 3*1 = 4 |
| 4*1 + 5*0 + 6*1 = 10 | 4*1 + 5*1 + 6*1 = 15 | 4*1 + 5*0 + 6*1 = 10 |
2. Element wise multiplication of two given arrays
In order to find the element-wise product of two given arrays, we can use the following function.
np.multiply(array a, array b)| A = | all | a12 | a13 |
| a21 | a22 | a23 |
| B = | a21 | a22 | a23 |
| a21 | a22 | a23 |
A*B =
| a11*b11 | a12*b12 | a13*b13 |
| a21*b21 | a22*b22 | a23*b23 |
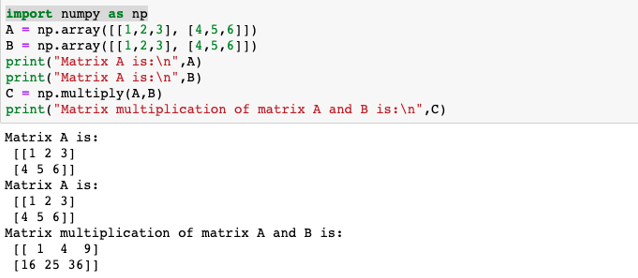
Example #2
Program to illustrate element-wise multiplication of two given matrices
Code:
import numpy as np
A = np.array([[1,2,3], [4,5,6]])
B = np.array([[1,2,3], [4,5,6]])
print("Matrix A is:\n",A)
print("Matrix A is:\n",B)
C = np.multiply(A,B)
print("Matrix multiplication of matrix A and B is:\n",C)The element-wise matrix multiplication of the given arrays is calculated in the following ways:
| A = | 1 | 2 | 3 |
| 4 | 5 | 6 |
| B = | 1 | 1 | 1 |
| 0 | 1 | 0 | |
| 1 | 1 | 1 |
A * B =
| 1*1 = 1 | 2*2 = 4 | 3*3 = 9 |
| 4*4 = 16 | 5*5 = 25 | 6*6 = 36 |
3. Scalar or Dot product of two given arrays
The dot product of any two given matrices is basically their matrix product. The only difference is that in dot product we can have scalar values as well.
| A= | a11 | a12 | a13 |
| B= | b11 |
| b12 | |
| b13 |
A.B = a11*b11 + a12*b12 + a13*b13
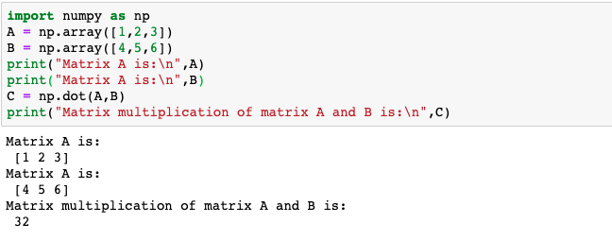
Example #3
A program to illustrate dot product of two given 1-D matrices
Code:
import numpy as np
A = np.array([1,2,3])
B = np.array([4,5,6])
print("Matrix A is:\n",A)
print("Matrix A is:\n",B)
C = np.dot(A,B)
print("Matrix multiplication of matrix A and B is:\n",C)The dot product of two given 1-D arrays is calculated in the following ways:
| A= | 1 | 2 | 3 |
| B= | 4 | 5 | 6 |
A.B = 1*4 + 2*5 + 3*6 = 32
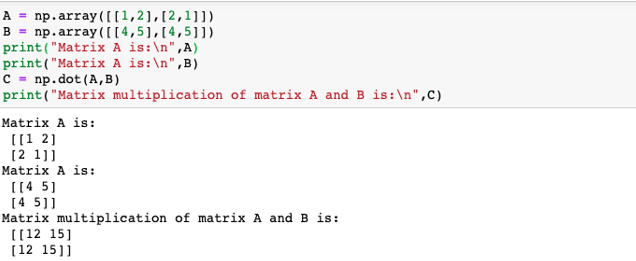
Example #4
A program to illustrate dot product of two given 2-D matrices
Code:
import numpy as np
A = np.array([[1,2],[2,1]])
B = np.array([[4,5],[4,5]])
print("Matrix A is:\n",A)
print("Matrix A is:\n",B)
C = np.dot(A,B)
print("Matrix multiplication of matrix A and B is:\n",C)The dot product of given 2D or n-D arrays is calculated in the following ways:
| A = | l | 2 |
| 2 | 1 |
| B= | 4 | 5 |
| 4 | 5 |
A.B =
| 1*4 + 2*4 = 12 | 1*5+2*5 = 15 |
| 2*4+ 1*4 = 12 | 2*5+ 1*5 = 15 |
Example #5
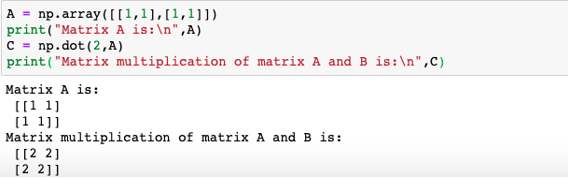
A program to illustrate the dot product of a scalar value and a 2-D matrix
Code:
A = np.array([[1,1],[1,1]])
print("Matrix A is:\n",A)
C = np.dot(2,A)
print("Matrix multiplication of matrix A and B is:\n",C)| A = | 1 | 1 |
| 1 | 1 |
Scalar value = 2
Then, np.dot(2,A) = 2* A
2*A =
| 1*2 = 2 | 1*2 = 2 |
| 1*2 = 2 | 1*2 = 2 |
Conclusion
Numpy offers a wide range of functions for performing matrix multiplication. If you wish to perform element-wise matrix multiplication, then use np.multiply() function. The dimensions of the input matrices should be the same. And if you have to compute matrix product of two given arrays/matrices then use np.matmul() function. The dimensions of the input arrays should be in the form, mxn, and nxp. Finally, if you have to multiply a scalar value and n-dimensional array, then use np.dot(). np.dot() is a specialisation of np.matmul() and np.multiply() functions.
Recommended Articles
This is a guide to Matrix Multiplication in NumPy. Here we discuss the different Types of Matrix Multiplication along with the examples and outputs. You can also go through our other related articles to learn more–