Updated July 28, 2023

Maturity Value Formula (Table of Contents)
- Maturity Value Formula
- Examples of Maturity Value Formula (With Excel Template)
- Maturity Value Formula Calculator
Maturity Value Formula
Maturity is the date on which the final payment for the financial instrument, like a bond, etc., happens, and there is no more payment that a borrower has to pay afterward.
So basically, all the interest and principal amount is paid in full at maturity, and the contract seizes to exist. For most securities like loans and bonds, the maturity value is the same as the per value, but different financial instruments have different definitions of maturity value. For example, Maturity for a swap transaction is the date of the final cash settlement. For commodity transactions, maturity is when the physical delivery of the commodity happens, etc. So the amount which the investor gets at the maturity date is known as maturity value. Maturity value also depends on the type of interest an investor is getting. The maturity value for simple interest will differ from that for compound interest.
Formula FOR Maturity Value:
As explained above, different financial instruments have different interpretations of maturity value.
- For Simple Interest Case, Maturity Value:
- For Compound Interest Cases and zero coupon bonds, the Maturity Value:
Where
- V – Maturity Value
- P – Principal Invested
- R – Rate of Interest
- T – Time of Investment
In the case of a bond that pays periodic coupon payments, the maturity value is the bond’s par value.
Examples of Maturity Value Formula (With Excel Template)
Let’s take an example to understand the calculation of the Maturity Value formula in a better manner.
Example #1
Let’s say you have invested a sum of $10,000 in a Bank for 5 years, and a bank is offering you 10% simple interest and 7.5% compound interest per year on this investment. You want to calculate the maturity value of this investment.
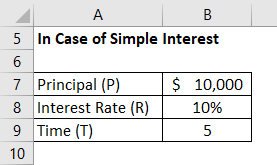
In Case of Simple Interest
Maturity Value is calculated using the formula given below
V = P * (1 + R * T)
- Maturity Value = $10,000 * (1 + 10% * 5)
- Maturity Value = $15,000
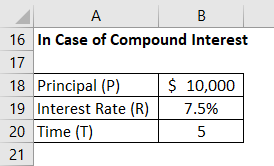
In the Case of Compound Interest
Maturity Value is calculated using the formula given below
V = P * (1 + R) ^ T
- Maturity Value = $10,000 * (1 + 7.5%) ^5
- Maturity Value = $14,356.29
Example #2
Continuing the above example, you have $10,000 to invest for 5 years, and now you have arranged a quotation from 3 different financial institutions:
- Institution 1: 9% interest compounded semi-annually
- Institution 2: 8.8% interest compounded quarterly
- Institution 3: 9% interest compounded monthly
Now you want to compare the maturity value of these investment proposals and then want to choose one among these three options. So:
Solution:
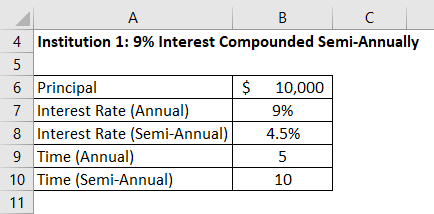
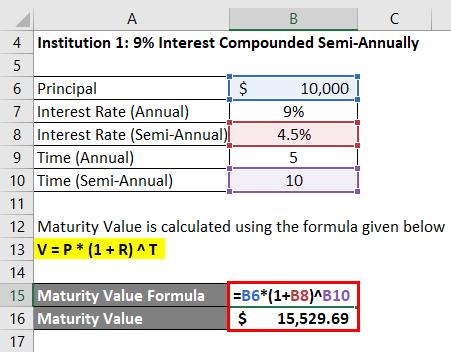
Institution 1: 9% Interest Compounded Semi-Annually
V = P * (1 + R) ^ T
- Maturity Value = $10,000 * (1 + 4.5%) ^ 10
- Maturity Value= $15,529.69
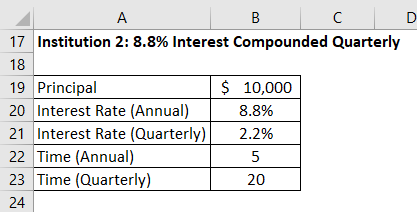
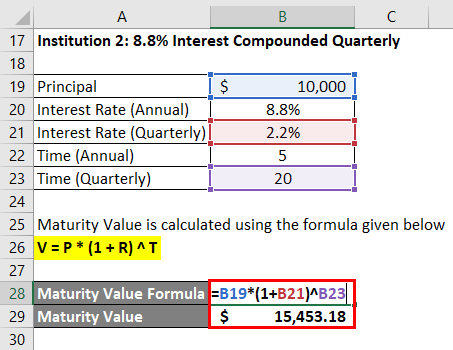
Institution 2: 8.8% Interest Compounded Quarterly
Maturity Value is calculated using the formula given below
V = P * (1 + R) ^ T
- Maturity Value = $10,000 * (1 + 2.2%) ^ 20
- Maturity Value = $15,453.18
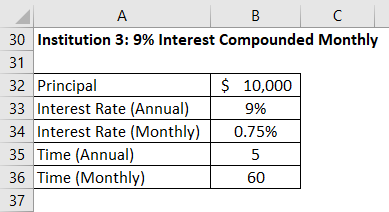
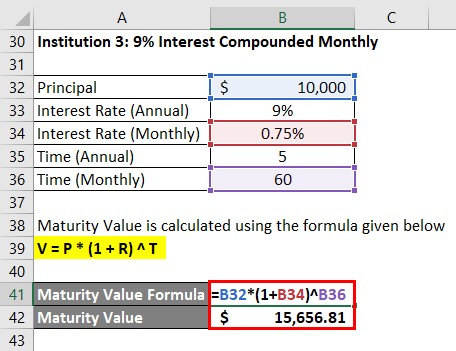
Institution 3: 9% Interest Compounded Monthly
V = P * (1 + R) ^ T
- Maturity Value = $10,000 * (1 + 0.75%) ^ 60
- Maturity Value = $15,656.81
So out of these three options, if you see, Institution 3 has the highest maturity value.
Explanation
As explained above, the maturity value is the value an investor will get at the contract’s expiration. Investors, before investing their money, can follow the following steps to determine the maturity value of the investment and then can compare different options to make the best decision:
- The first step is determining what type of interest you will earn on the investment. Compound interest will result in a higher maturity value than a simple interest rate if the rate of interest is the same.
- Secondly, in the case of compound interest, investors will also have to look at the frequency of the compounding because the frequency of compounding has a direct impact on the maturity value. The higher the frequency, the higher will be the maturity value. For example, monthly compounding will have a higher maturity value than semiannual compounding, given the same rate.
- Once all the above steps are taken care of, investors can simply use the maturity value formula and calculate the maturity value.
As discussed earlier, the nature of the financial instrument also affects the maturity value. Bonds that pay coupons will have a maturity value that equals its par value because all the interest is paid through coupons.
Relevance and Uses
Since maturity value is the amount that an investor will get at the contract’s maturity, this is a very useful concept that helps investors see the worth of their investment. They can compare the maturity value of various financial instruments, which will help them make an informed decision. Also, when an investor chooses investments that pay compound interest, they earn interest on the interest because their maturity value gets the compounding effect. But investors should be very careful when choosing a financial instrument and not decide only based on maturity value. Just because an investment is given a higher maturity value does not guarantee that you will receive that money, and there is a probability that the borrower can default. So along with the maturity value, the credit history of a borrower and other factors are also important, and an investor should take care of that also.
Maturity Value Formula Calculator
You can use the following Maturity Value Calculator
| P | |
| R | |
| T | |
| Maturity Value Formula | |
| Maturity Value Formula = | P * (1 + R)T |
| = | 0 * (1 + 0)0 = 0 |
Recommended Articles
This has been a guide to Maturity Value Formula. Here we discuss how to calculate Maturity Value along with practical examples. We also provide a Maturity Value calculator with a downloadable Excel template. You may also look at the following articles to learn more –