Updated July 29, 2023

What is the Median Formula?

The median formula finds the middle value in a set of data, i.e., the middle number in a set of numbers. It tells us where the center of the data is, which can be helpful in different scenarios like studying temperatures, analyzing student scores, or finding the central age in a population.

The median formula is useful when a dataset is uneven or has extreme numbers (values that are much higher or lower than the others). In such cases, other methods, like the mean, can give a less accurate result as extreme values can influence the center value. However, the median formula is less affected by these outliers and provides a more precise estimate of the middle value.

We can calculate the median using a simple mathematical formula:

Median = (n + 1) / 2

Where “n” represents the total number of items, i.e., the total number of values present in the dataset.

Note: This formula helps us find the position of the median in the dataset rather than the actual value of the median.

How to Calculate Median in Excel?

We can use the built-in function called “MEDIAN” to calculate the median in Excel.

The syntax for the MEDIAN function is as follows:

We can use the MEDIAN function in two ways:

1. Range of Dataset

Here, we must add the cell range for the data in the function as the first argument.

For example, if our data is present in the cells A2 to A 10, we will write the MEDIAN function as:

=MEDIAN(A2:A10)

2. Array of Data

In this approach, we directly provide all the dataset values to the MEDIAN function in the form of an array. You can use this method when the dataset is small, or else directly selecting the range is an easy option.

For example, if our dataset has the following values: 2,4,6,8,10, our MEDIAN function will be:

=MEDIAN(2,4,6,8,10)

Note: Unlike the mathematical formula for calculating the median, the MEDIAN Excel function gives the actual value of the median rather than the position.

Examples of Median Formula

Let’s take a look at some examples of median formulas. We have provided examples of both the Simple median formula as well as MEDIAN function in Excel.

1. Simple Median Formula

Example: Odd number of observations
Example: Even number of observations

2. MEDIAN Function in Excel

Example: Dataset with an Odd number of Values
Example: Dataset with an Even number of Values

We have included an Excel template with solved examples to help you better understand how to use the median function and formula in Excel.

You can download this Median Excel Template here – Median Excel Template

1. Simple Median Formula Examples

Example #1: Odd Number of Observations

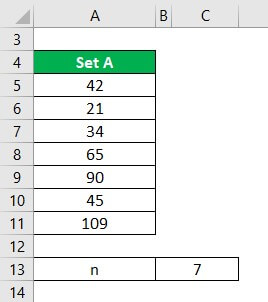
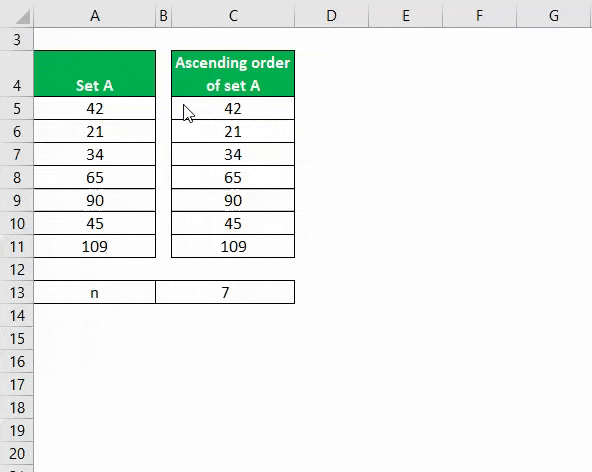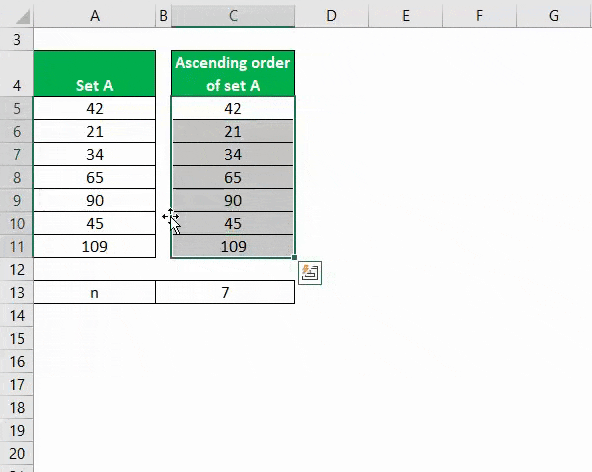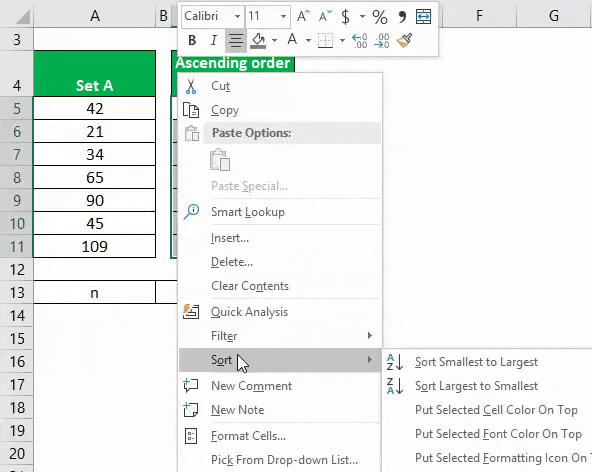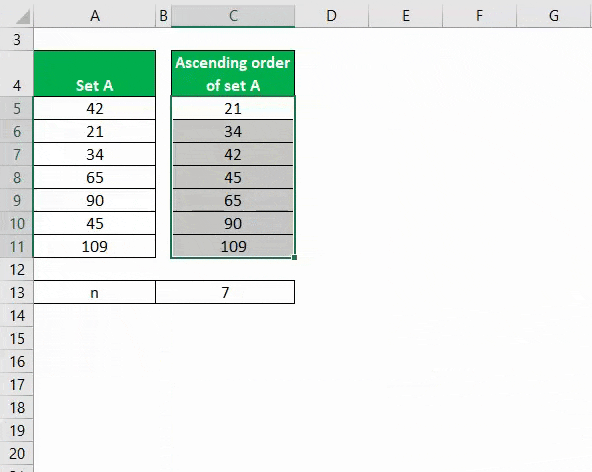
Calculate the Median for the dataset: A= 42, 21, 34, 65, 90, 45, 109. As the number of values in the dataset is 7, n will be 7.

Given,

Solution:

Step 1: Sort the Data in Ascending Order
It’s important to sort the dataset in ascending order before we find the median.
So, first, select the range of cells you want to sort. As per our dataset, we will select cells A5 to A11.
To sort the data from the smallest to the highest number, you have 2 options:

1. Go to the Data tab -> Sort & Filter group-> click on Sort.
OR
2. Right-click over the selected data -> choose Sort -> Click “Sort Smallest to Largest”.

Step 2: Find the Median’s Position in the Data Set
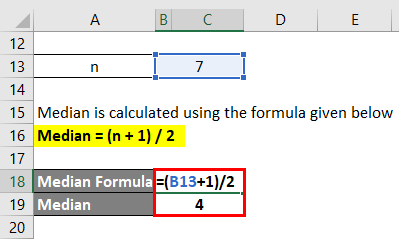
We can calculate the median’s position using the following formula:
Median = (n + 1) / 2
= (7 + 1) / 2 = 8 / 2 = 4

Step 3: Find the Median Value
As the position of the median value in the dataset is 4. We must check what is the 4th item in the dataset. In our dataset, the 4th item is 45.
Therefore, the median value for the dataset sorted in ascending order (21, 34, 42, 45, 65, 90, 109) is 45.

Example #2: Even Number of Observations

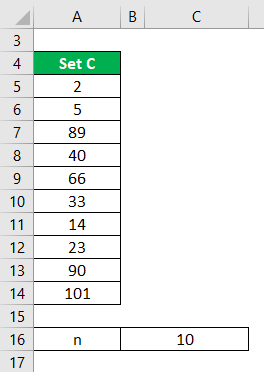
Let us calculate the median for the given dataset: B= 2, 5, 89, 40, 66, 33, 14, 23, 90, 101. As there are 10 observations in our dataset, n will be 10.

Solution:

Step 1: Sort the Data
Sort the data in the dataset in ascending order (you can follow any of the methods shown in Example #1).

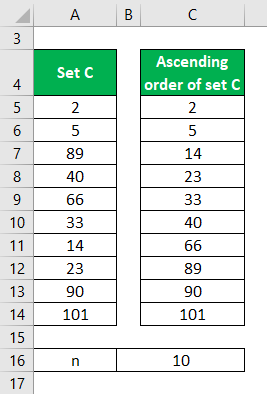
Step 2: Find the Median’s Position in the Data Set
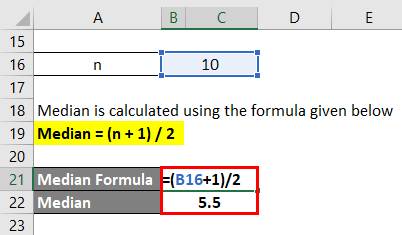
Now, we will calculate the median’s position using the below formula,
Median = (n + 1) / 2
=(10 + 1) / 2 = 11 / 2
Median = 5.5

Step 3: Find the Median

Since the position of the median is 5.5, it means the median value is the average of the values present at the 5th and 6th positions of the dataset.
As per our dataset arranged in ascending order (2, 5, 14, 23, 33, 40, 66, 89, 90, 101), the 5th and 6th values are 33 and 40, respectively.
To find the average of 33 and 40, we must add both numbers and divide the result by 2.
Median = (33 + 40)/2 = 73/2 = 36.5

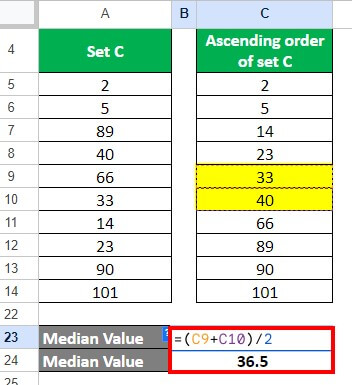
Thus, the median value for the dataset is 36.5.

2. MEDIAN Function in Excel Examples

Example #1: Dataset with Odd Number of Values

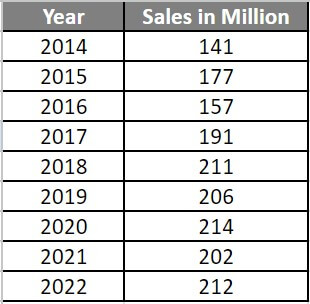
A company has the following sales data for the years 2014 to 2022.

Year	2014	2015	2016	2017	2018	2019	2020	2021	2022
Sales	141	177	157	191	211	206	214	202	212

Let us find the median for the above data using the MEDIAN function.

Given,

Solution:
While using the MEDIAN function, there is no need to sort the data in ascending order. The function does this automatically before finding the median.

Step 1: To find the median, add the following formula in the cell B12:

=MEDIAN(B2:B10)

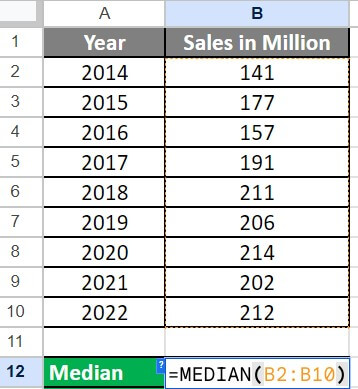
Step 2: Press “Enter”. The MEDIAN function finds and returns the median value.

Here, the function returns 202 as the median value for the given range (B2:B10).

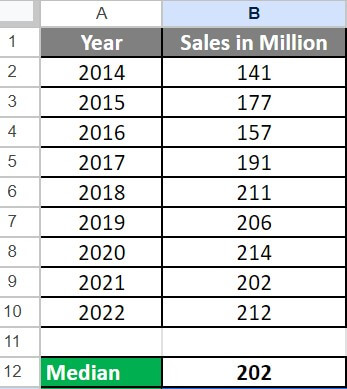
So, the median for the given sales data is 202.

Example #2: Dataset with an Even Number of Values

Let us find the median value for the following data using the MEDIAN function.
C = 13, 25, 12, 40, 27, 80, 55, 62, 99,73

Solution:
Step 1: Enter the folding formula in the cell B13:

=MEDIAN(13, 25, 12, 40, 27, 80, 55, 62, 99,73)

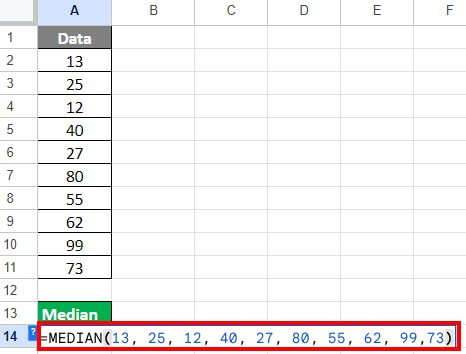
Step 2: Press “Enter”. The MEDIAN function will calculate and return the middle value.
Here, the function returns the value of 47.50. It is the average between the two middle values of the dataset (40 and 55).

Basically, the function found the two middle values, 40 and 55, and found their average: (40 + 55) /2 = 47.5.

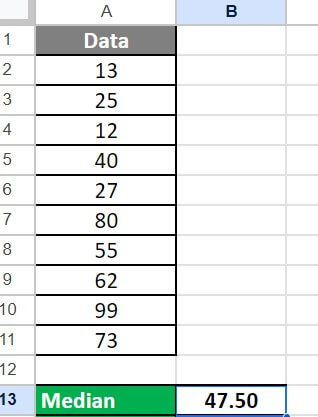
Therefore, the median for the dataset (13, 25, 12, 40, 27, 80, 55, 62, 99,73) is 47.5.

Things to Keep in Mind

1. Use the COUNTA function to find the value for ‘n’:
If you want to find the number of values in a large dataset containing hundreds or thousands of values, you can use the COUNTA function to find the ‘n’ value.

Example: Let’s say you want to find the median for a dataset present in cells A1 to A1000. To quickly and easily find the value for ‘n’, you can use the formula: =COUNTA(A1:A1000)

2. The MEDIAN function automatically neglects the empty cells and text:
While calculating the median, the MEDIAN function will automatically ignore any cell with a non-numeric value, i.e., if the cell has text or is empty.

Example: Suppose we have a dataset in cells A1 to A7, where A3 is empty, and A6 contains the text “eduCBA”, the formula “=MEDIAN(A1:A7)” will only consider the numeric values (1, 2, 4, 5, 7) and ignore the empty cell and text.

3. The MEDIAN function counts the logical values:
The MEDIAN function takes into account logical values (TRUE and FALSE) during the calculation. TRUE is treated as 1, while FALSE is treated as 0.

Example: If you use the MEDIAN function for the dataset: FALSE, 5, TRUE, 2, the median will be 3. It is the average of the two middle values, 5 and TRUE (equivalent to 1). However, if the dataset was FALSE, 5, 2, the median would be 5 (not 3).

Importance and Uses of Median Formula

The Median is the point where 50% of the numbers are above & 50% of the numbers are below. It is a centrality denoting the middle value, which is helpful for a historical dataset or data set over time.
It is advantageous when the data set includes very high and low values or the data in the group is mixed (texts, empty values, numbers, etc.).
Economists use median values to draw conclusions and frame economic policies. For instance, they can determine the median price of houses in a specific area to see if houses in that area are affordable or expensive.

Median Formula Calculator

Use the following medium calculator for calculating the median.

n
Median Formula

Median Formula =

(n + 1)
	=
2

(0 + 1)
	=	0
2

Frequently Asked Questions(FAQs)

Q1. What is n in the median formula?
Answer: The variable “n” in the median formula represents the total number of values in the dataset. For example, if you have the following dataset of 7 values:
3, 5, 1, 4, 6, 8, 2
The value of “n” would be 7 because there are 7 values in the dataset.

Q2. What is the relationship between mean, mode, and median?
Answer: In statistics, the mean, median, and mode have a connection known as the empirical relationship. It means that if we know the value of any of the two metrics, we can find the value of the remaining one. We can use the following equation to find this:

Mode = 3 x Median – 2 x Mean

For example, if the median value is 4 and the mean value is 3, we can find the mode value.
Mode = (3 x 4) – (2 x 3) = 12 – 6
Mode = 6

Q3. What are the two formulas of median?
Answer: We have two formulas for the median, i.e., the odd number of observations and the even number of observations.

If the number of terms(n) is even, then the formula is ½ [(n/2)+((n/2)+1)]
If the number of terms(n) is odd, then the formula is (n+1)/2

Q4. What is the conditional median formula?
Answer: If you want to find the median for a group of data based on a condition, you can use the conditional median formula. For instance, if you want to find the median for all values that are below 100, we can use the conditional median formula. Here we use the IF function combined with the MEDIAN function. The IF function checks if a given condition is true for each value in the dataset. If the condition is true, the MEDIAN function includes that value when determining the median of the dataset.

The syntax is as follows:

MEDIAN (IF(criteria_range = criteria, median_range))

Quiz Result
Total Questions	Correct Answers	Wrong Answers	Percentage