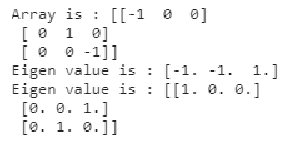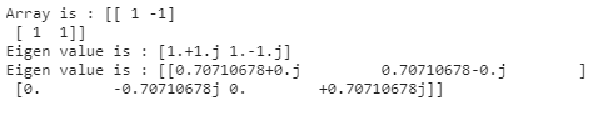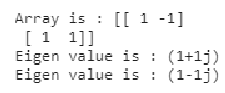Updated April 12, 2023

Definition of Numpy Eigenvalues
Numpy Eigenvalue is a function in the numpy linear algebra package of the numpy library which is used to generate the Eigenvalues or Eigenvectors from a given real symmetric or complex symmetric array or matrix given as input to the function. Depending upon the kind of input array or matrix the numpy eigenvalue function returns two type of arrays, one dimensional array representing the eigenvalues in the position of the input and another two dimensional array giving the eigenvector corresponding to the columns in the input matrix.
Syntax:
The numpy eigenvalue function basically called using the syntax,
numpy.linalg.eigvals(a)- Linalg.eigvals represents the linear algebra package in the numpy library which is used to perform various algebraic operations
- Parameter ‘a’ is the input array or matrix which is complex or real values.
- The function returns the eigenvalues which are not in ordered manner and represented to its own variety. If the computation of the eigenvalues does not align it throws us an error.
Examples of Numpy Eigenvalues
Following are the examples are given below:
Example #1
Code:
import numpy as np
# Generating an array using numpy array function
a = np.array([[3, -1j], [1j, 3]])
print("Array is :",a)
# using linear algebra package
# eigen value function is implemented
x, y = np.linalg.eigh(a)
print("Eigen value is :", x)
print("Eigen value is :", y)Output:
In this example we have an input array of complex value ‘a’ which is used to generate the eigenvalue using the numpy eigenvalue function. As we can see in the output we got two arrays of one dimension and two dimensions. First array is the eigenvalue of the matrix ‘a’ and the second array is the matrix of the eigenvectors corresponding to the columns.
Example #2
In this example we will determine the eigenvalues of the simple diagonal matrix and we will generate the corresponding eigenvector.
Code:
import numpy as np
# Generating a diagonal matrix using numpy array function
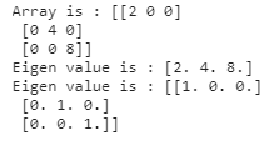
a = np.diag((2, 4, 8))
print("Array is :",a)
# using linear algebra package
# eigen value function is implemented
x, y = np.linalg.eigh(a)
print("Eigen value is :", x)
print("Eigen value is :", y)Output:
In this example we have used a real value matrix which is diagonal and we have tried to calculate the eigenvalue of that matrix. The input matrix is 3×3 diagonal matrix and hence the eigenvalues are the real numbers that are non zero in the matrix which is (2,4,8). The corresponding eigenvector for the diagonal matrix is generated.
Example #3
Code:
import numpy as np
# Generating an diagonal matrix using numpy array function
a = np.diag((-1,1,-1))
print("Array is :",a)
# using linear algebra package
# eigen value function is implemented
x, y = np.linalg.eigh(a)
print("Eigen value is :", x)
print("Eigen value is :", y)Output:
similar to the previous example we have created a diagonal matrix of values (-1,1,-1) which has real values and we calculated the eigenvalue of the matrix and all the real values in the matrix corresponds to the eigenvalue and the corresponding eigenvector for the diagonal matrix is created.
Example #4
Code:
import numpy as np
# Generating a 2-D matrix using numpy array function
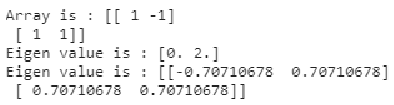
a = np.array([[1, -1], [1, 1]])
print("Array is :",a)
# using linear algebra package
# eigen value function is implemented
x, y = np.linalg.eigh(a)
print("Eigen value is :", x)
print("Eigen value is :", y)Output:
Code:
import numpy as np
# Generating a 2-D matrix using numpy array function
a = np.array([[1, -1], [1, 1]])
print("Array is :",a)
# using linear algebra package
# eigen value function is implemented
x, y = np.linalg.eig(a)
print("Eigen value is :", x)
print("Eigen value is :", y)Output:
In this example we have compared the numpy linalg.eigh() and linalg.eig() functions, where the linalg.eigh() is used to generate the eigenvalues and eigenvectors of the complex conjugate matrix or real symmetric matrix. The
linalg.eig() function is used to computing the eigenvalues and eignvectors of the input square matrix or an array.
We have created a two dimensional array ‘a’ and used the linalg.eigh() and linalg.eig() functions to generate the eigenvalues and vectors for the input matrix ‘a’ we can see the difference in both the outputs. The linalg.eig() function returns us the complex conjugate of the input array ‘a’ and linalg.eigh() which takes the complex symmetric matrix as input gives us the eigenvalues and vectors corresponding to the input array.
Example #5
Code:
import numpy as np
# Generating an 2_D matrix using numpy array function
a = np.array([[1,-1], [1, 1]])
print("Array is :",a)
# using linear algebra package
# eigen value function is implemented
x, y = np.linalg.eigvals(a)
print("Eigen value is :", x)
print("Eigen value is :", y)Output:
In this example we have used the linalg.eigvals() function which is different from the linalg.eig() function where the former return only the eigenvalues and does not return us the eigenvectors as we can see in the output.
Example #6
Code:
import numpy as np
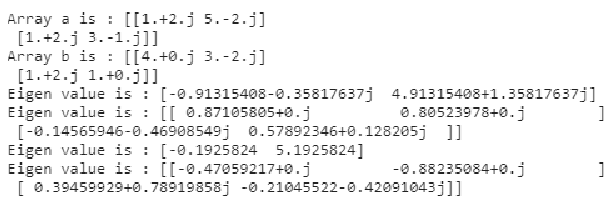
a = np.array([[1+2j, 5-2j], [1+2j, 3-1j]])
print("Array a is :",a)
b = np.array([[4.+0.j, 3.-2.j], [1.+2.j, 1.-0.j]])
print("Array b is :",b)
# using linear algebra package
# eigen value function is implemented
x1,y1 = np.linalg.eig(a)
x2,y2 = np.linalg.eigh(b)
print("Eigen value is :", x1)
print("Eigen value is :", y1)
print("Eigen value is :", x2)
print("Eigen value is :", y2)Output:
In this example for a clearer understanding of the numpy linalg.eig() and linalg.eigh() function we have created two arrays ‘a’ & ‘b’ as input array and used the linalg.eig() and linalg.eigh() function to generate the eigenvalues and eigenvectors for both the arrays. Where we can see the eigenvalues and vectors of complex or real symmetric matrices are always real values.
Conclusion
In this article, we have discussed Numpy eigenvalues function in detail using various examples to get a clear understanding on the numpy eigenvalues function and its uses. We have also discussed in detail of how to use numpy linear algebra package to call the eigenvalues functions and also the difference in different eigenvalue functions like eig(), eigh() and eighvals() in the linear algebra package. We also discussed about the techniques involved in using real and complex arrays as input in calculating the eigenvalues and vectors.
Recommended Articles
This is a guide to Numpy Eigenvalues. Here we also discuss the definition and syntax of numpy eigenvalues along with different examples and its code implementation. You may also have a look at the following articles to learn more –