Updated April 12, 2023
Definition of NumPy random normal
The NumPy random normal() function is used to gets the random samples from a normal distribution. The NumPy random normal() function is a built-in function in NumPy package of python. The NumPy random normal() function generate random samples from a normal distribution or Gaussian distribution, the normal distribution describes a common occurring distribution of samples influenced by a large of tiny, random distribution or which occurs often in nature. The normal distribution also called a bell curve because of its shape and these samples of distribution are commonly used in data statistics, data analysis, data-related fields, and all and also can be used in probability, machine learning, Bayesian statistics, and all. It is the most important distribution.
Syntax:
NumPy.random.normal(loc = 0.0, scale = 1.0, size = None)Parameters:
- loc – This is an optional parameter, which specifies the mean (peak) of distribution. The default value is 0.0.
- scale – This is an optional parameter, which specifies the standard deviation or how flat the distribution graph should be. The default value is 1.0.
- size – This is an optional parameter, which specifies the shape of the resultant array. The default value is 1.
- Return value – The return value of this function is the NumPy array of random samples from a normal distribution.
Working of the NumPy random normal() function
The NumPy random normal() function accepts three parameters (loc, scale, size) and all three parameters are not a mandatory parameters. If we pass nothing to the normal() function it returns a single sample number. If we pass the specific values for the loc, scale, and size, then the NumPy random normal() function generates a random sample of the numbers of specified size, loc, and scale from the normal distribution and return as an array of dimensional specified in size.
Examples
Example of NumPy random normal() function for generating samples from a normal distribution –
Next, we write the python code to understand the NumPy random normal() function more clearly with the following example, where the normal() function is used to generating samples of size six from a normal distribution, as below –
Example #1
Code:
# import numpy package as np
import numpy as np
# Using normal() method of random class
ndis_no = np.random.normal(size = 6)
print( "The output of random normal for loc=0.0, scale=1.0 and size=6 is : " )
# printing the size 6 normal distribution random samples of the normal() function
print( ndis_no )
print("\n")
ndis_no = np.random.normal( loc=0.5, scale=1.5, size = 6)
print( "The output of random normal for loc=0.5, scale=1.5 and size=6 is : " )
print( ndis_no )Output:
Again when we run the above program it will generate another sample random number, as we can see below –
As in the above program, the loc, scale, and size(single-dimensional) values are passed to the normal() function, so the normal() function is generating the random samples from the normal distribution according to the passed values. In the above output if we see every time it generating the different random samples.
Example for generating multidimensional samples from a normal distribution –
Next, we write the python code to understand the NumPy random normal() function, where the normal() function is used to generating multidimensional samples of size (3, 5) and (2, 5) from a normal distribution, as below –
Example #2
Code:
# import numpy package as np
import numpy as np
# Using normal() method of random class
ndis_no = np.random.normal(size = (3,5))
print( "The output of random normal for loc=0.0, scale=1.0 and size=(3, 5) is : " )
# printing the size 6 normal distribution random samples of the normal() function
print( ndis_no )
print("\n")
ndis_no = np.random.normal( loc =0.5, scale =1.5, size =(2,5))
print( "The output of random normal for loc=0.5, scale=1.5 and size=(2, 5) is : " )
print( ndis_no )Output:
Again, when we run the above program it will generate another sample random number, as we can see below –
As in the above program, the loc, scale, and size(two dimensional(3, 5), where 3 is the number of rows and 5 is the number of columns) values are passed to the normal() function, so the normal() function is generating the random samples from the normal distribution according to the passed values. In the above output if we see every time it generating the different random samples.
Example of NumPy random normal() function for generating samples from a normal distribution and plot them-
Next, we write the python code to understand the this function, where the normal() function is used to generating multidimensional samples of size five hundred from a normal distribution and plot them, as below –
Example #3
Code:
# import numpy package as np
import numpy as np
# import pyplot as plt
from matplotlib import pyplot as plt
# Using normal() method of random class
mean_value = 0.0
std_value = 1.0
ndis_no = np.random.normal( mean_value, std_value, size = 500 )
print( "The output of random normal for loc=0.0, scale=1.0 and size = 500 is : " )
# printing the size 6 normal distribution random samples of the normal() function
print( ndis_no )
count, bins, ignored = plt.hist( ndis_no, 50)
plt.show()Output:
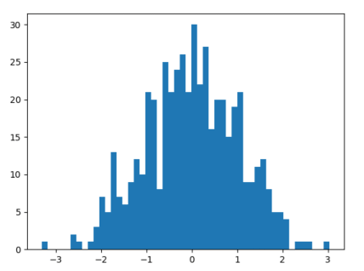
And the plot of above five hundred numbers, as we can see below –
As in the above program, the normal() function is generating the five hundred random sample numbers from the normal distribution according to the passed values and which are plotting as well using the matplotlib package In the above output if we see the distribution of the sample numbers is normal distribution as it is having bell shape.
Conclusion
The NumPy random normal() function is a built-in function in the NumPy package, which is used to gets the random samples of a specified dimensional array from the normal distribution.
Recommended Articles
This is a guide to NumPy random normal. Here we also discuss the Description, syntax, parameters, Working of the NumPy random normal() function and different examples, and its code implementation. You may also have a look at the following articles to learn more –