Updated April 7, 2023

Introduction to OpenCV Kalman filter
OpenCV Kalman filter is a class of method used to implement the standardized Kalman filter. Let us first have a look at what is the use of the Open CV Kalman filter. It is predefined, which is used to equate for an algorithm that is known to use a series of observed measurements taken over an observational time period. This data set contains data related to statistical noise and other related inaccuracies.
This filter thereby tends to produce much more estimates with respect to unknown variables compared to that of the estimates are calculated on the basis of single measurements. This happens because while producing the results, the estimation is made on the basis of distribution for the joint probability with respect to the variables that are taken over the suggested period of time. this filter is also known as the linear quadratic estimation filter used in the fields of statistical analysis and control measurement. the filter was pioneered by Rudolph Kalman, who is one of the most prominent to establish this theory.
Note: However, the developers can modify the values of transitionMatrix, measurementMatrix, and to have an extension over the functionality for the Kalman filter.
The syntax for the OpenCV Kalman filter
The following is the syntax that is used for implementing or using the Open CV Kalman filter method:
<KalmanFilter object> = cv . KalmanFilter ( dynamParams, measureParams[, controlParams[, type]]cv::KalmanFilter::KalmanFilter ( int dynamParams, int measureParams, int controlParams = 0, int type = CV_32F )Parameters for OpenCV Kalman filter
The following is the parameters are used while implementing or using the Open CV Kalman filter method:
|
Parameters |
Description |
|
dynamParams |
The parameter describes the dimensional state of the data set or the algorithmic matrix that has been provided. |
|
measureParams |
The parameter describes the dimensionality of the measurement index, which further describes the data set or the algorithmic matrix that has been provided. |
|
controlParams |
The parameter describes the dimensionality of the vectors that are used as a control set for the experimental results to be derived. |
|
Type |
The parameter describes the type of data set that the resultant matrices that would be created as the operation of the method would be(meaning either CV_32F or CV_64F) |
Examples of the Use of Kalman filter
The following example is used to demonstrate how the two-dimensional tracker works, which is more immune to the noise in the system dynamics. For this, the Kalman filter main code is set with 4 parameters that operate dynamically 2 parameters used for measurement, which is not specific to control set up. The tracker measurements are 2-D object location, while the dynamic variables are the two-dimensional velocity and location.
KalmanFilter KF1(40, 20, 0);
KF1.transitionMatrix = *(Mat_<float>(40, 40) << 1,0,1,0, 0,1,0,1, 0,0,1,0, 0,0,0,1);
Mat_<float> measurement(2,1); measurement.setTo(Scalar(0));
// init...
KF1.statePre.at<float>(0) = mouse_info.x;
KF1.statePre.at<float>(1) = mouse_info.y;
KF1.statePre.at<float>(2) = 0;
KF1.statePre.at<float>(3) = 0;
setIdentity(KF1.measurementMatrix);
setIdentity(KF1.processNoiseCov, Scalar::all(1e-4));
setIdentity(KF1.measurementNoiseCov, Scalar::all(1e-1));
setIdentity(KF1.errorCovPost, Scalar::all(.1));
// First predict, to update the internal statePre variable
Mat prediction1 = KF1.predict();
Point predictPt(prediction.at<float>(0),prediction.at<float>(1));
// Get mouse point
measurement(0) = mouse_info.x;
measurement(1) = mouse_info.y;
Point measPt(measurement(0),measurement(1));
// The "correct" phase that is going to use the predicted value and our measurement
Mat estimated = KF1.correct(measurement);
Point statePt(estimated.at<float>(0),estimated.at<float>(1));Output for OpenCV Kalman filter example:
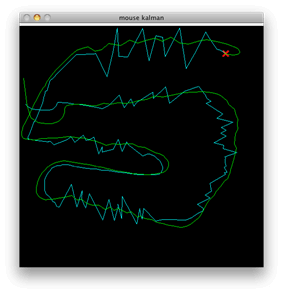
For the following output, the mouse has been set to have a callback and derive a mouse’s position for each frame (every frame consisting of a time-lapse of 100 milli seconds), and the same is fed into the filter as dynamic data.
While not using velocity as a vector variable, the output of the code displays the stark difference.
How does the Kalman Filter work?
Let us look at the scenario we are trying to evaluate, considering a simple state with only a relevant position and counterpart velocity.
x⃗ =[pv]But we are not aware about the actual position and actual velocity for the scenario. Thus there arises a wide range of possible combinations of velocities and positions that may turn out to be true; alas, some have a greater chance of likelihood over others.
While making the Kalman filter, it assumes that both variables (in the given case position and velocity) are chosen at random and follow the principle of Gaussian distribution. Each variable is designated with a mean value (μ), which stands as the centre for the randomized distribution to occur. Each variable is also designated with a variance (σ2), which is representative of the uncertainty:
Conclusion
The Kalman filter serves as a very powerful tool, especially when it comes to interacting and working with very noisy systems. The Kalman filter’s holistic approach is to process the Noisy data into the system and process out less noisy data. There are numerous applications to the Kalman filter which are for utilization in algorithm designing of tracking devices and objects (such as missiles, automobiles, face detection, hands or complete human figure), used for pointing data to detect mass noisy patches, used in the field of economics, majorly used for motions detection and navigation, used extensively in a lot of computer and tech-based vision applications, used to stabilize measurements for depths and heights and feature tracking access making wide use and development of stereo-cameras used for velocity and depth measurements.
Recommended Articles
We hope that this EDUCBA information on “OpenCV kalman filter” was beneficial to you. You can view EDUCBA’s recommended articles for more information.