Updated July 6, 2023
Introduction to Pandas quantile
Pandas quantile() work return esteems at the given quantile over a mentioned pivot, a numpy.percentile. In every arrangement of estimations of a variate that isolate a recurrence appropriation into equivalent gatherings, each containing a similar part of the all-out populace.
Python is an incredible language for information investigation, essentially because of the phenomenal biological system of information-driven Python bundles. Pandas is one of those bundles that simplifies bringing in and breaking down information.
Syntax and Parameters:
pandas.dataframe.quantile(axis=0,q=0.5, interpolation='linear',numeric_only=True)Where,
axis represents the rows and columns. If axis=0, it represents the rows; if axis=1, it represents the columns.
q represents quantile. It is always 0.5, which is 50%. So, if the quantile value is greater than 0 and less than 1, then the quantile will be implemented.
numeric_only represents all the numeric values that have to be assigned to get the data implemented. If False, the quantile of datetime and timedelta information will be registered too.
Interpolation is always assigned to linear by default.
It returns q as an array, a DataFrame will be returned where the file is q, the sections are simply the segments, and the qualities are the quantiles. If q is afloat, a Series will be returned where the record is simply the sections, and the qualities are the quantiles.
How Does quantile() Function Work in Pandas?
Now we see various examples of how the quantile() function works in Pandas.
Example #1
Using the quantile() function to implement the result from the axis.
Code:
import pandas as pd
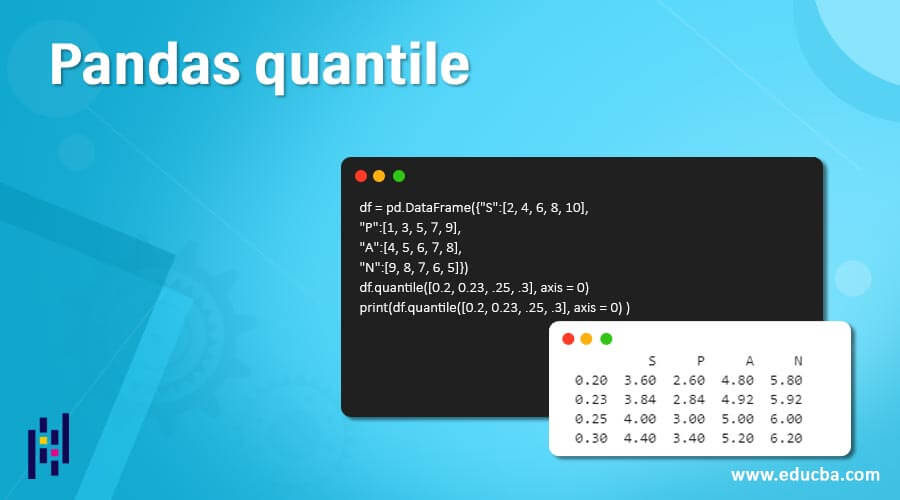
df = pd.DataFrame({"S":[2, 4, 6, 8, 10],
"P":[1, 3, 5, 7, 9],
"A":[4, 5, 6, 7, 8],
"N":[9, 8, 7, 6, 5]})
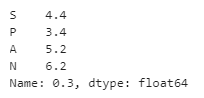
df.quantile(0.3, axis = 0)
print(df.quantile(0.3, axis = 0) )Output:
In the above program, we import the panda’s library as pd and then define the dataframe. After creating the dataframe, we use the quantile() function to assign and create values along the row axis, as shown in the above program. The program is finally implemented, and the result is as shown in the above snapshot.
Example #2
Using the quantile() function to implement the result of multiple quantile values in the axis.
Code:
import pandas as pd
df = pd.DataFrame({"S":[2, 4, 6, 8, 10],
"P":[1, 3, 5, 7, 9],
"A":[4, 5, 6, 7, 8],
"N":[9, 8, 7, 6, 5]})
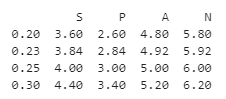
df.quantile([0.2, 0.23, .25, .3], axis = 0)
print(df.quantile([0.2, 0.23, .25, .3], axis = 0) )Output:
In the above program, we import pandas as pd and then define the dataframe. After defining the dataframe, we use the quantile() function to assign multiple quantile values along the row axis. Hence, we assign the axis value to 0, as shown in the above program. Thus, we implement the program; the above snapshot shows the output.
We will actualize the quantile standardization calculation step-by-by with a toy informational collection. We will then wrap that as a capacity to apply a reproduced dataset. At last, we will instance a couple of representations to perceive how the information looked when quantile standardization. To accomplish standardization, we compel the observed appropriations to be the same. The normal dissemination, obtained by taking the normal of each quantile across tests, is utilized as the reference.
The initial phase in performing quantile standardization is to sort every section autonomously, including each example. To sort all the segments freely, we use NumPy sort() to work on the qualities from the dataframe. Since we lose the section and list names with Numpy, we make another dataframe utilizing the arranged outcomes with record and segment names. These mean qualities will supplant the original information in every segment, with the end goal that we save the request for every perception or feature in Samples/Columns. This essentially powers all the examples to have similar dispersions. Note that the mean qualities in the rising requests, the main worth is the most minimal position, and the latter is the most noteworthy position. Let us change the record to mirror that the mean we registered is positioned from low to high. To do that, we use list work relegate positions arranged from 1. Note our list begins at 1, mirroring that it is a position. This is how quantile standardization works in Pandas.
Conclusion
Hence, quantile standardization is a measurement technique that can help investigate high-dimensional datasets. One of the fundamental objectives of performing standardization like Quantile standardization is to change the crude information to expel any undesirable variety because of specialized antiques and safeguard the real variety that we are keen on examining. Fields like genomics generally embrace quantile standardization, but it can be helpful in any high-dimensional setting.
Recommended Articles
We hope that this EDUCBA information on “Pandas quantile” was beneficial to you. You can view EDUCBA’s recommended articles for more information.