Updated April 12, 2023

Definition of Python Perfect Number
Perfect number in python is defined as an implementation that is built in python where the number which is required to search for being perfect is broken down into factors, and then the factors are summed over excluding the actual number itself and then checked if the sum of the factors obtained is equal to the original number itself. If the sum is equal to the actual number, the number is termed a perfect number. The concept of the perfect number dates back to as early as 300 BC during Euclid’s era, and the concept comes from Greek numerology. In this article, we will understand the implementation of perfect numbers in python and also understand the bit of mathematics behind the logic of a number being a perfect number. We will also understand pseudocode in python before we move on to the coding genre of the perfect number.
The logic behind Perfect number
In this section, we will try to understand the logic behind a number being adjudged as a perfect number both mathematically and look at the pseudo-code of adjudging a number to being a perfect number. So, let’s start off at looking at it mathematically first.
Euclid, in 300 BC, proved that any number of the form 2P−1(2P − 1) is termed as a perfect number if the factor (2P − 1) is a prime number. In a number line, 6 is the smallest perfect number. Let us see how. For P = 2, the value of 2P−1(2P − 1) is 6 and (2P − 1) for P=2 is 3. Let us see the same thing logically. The divisors of 6 are 1, 2, 3, and 6. Now, as per the rule, if we ignore the number itself, we are left with divisors 1, 2, and 3. Now, let us find the summation of the 3 divisors. 1 + 2 + 3 = 6. The sum is equal to the original number itself, and hence 6 is a perfect number. Just as trivia, if the sum of divisors is less than the original number, they are known as deficient, and if the sum is greater than the number itself, the number is named as abundant. For example, divisors of 8 are 1, 2, 4, and 8, and summation of 1, 2, and 4 is 7. Thus 8 is a deficient number. For example, number 40’s divisors are 1, 2, 4, 5, 8, 10, 20, and 40. The summation of all divisors except the number itself is 50, and hence 40 is abundant. Going back to the topic from trivia, one would argue that for P = 4, we have a value of 2P−1(2P − 1) = 120, but 120 is not perfect, and that is just because (2P − 1) = 15 is not a prime number and hence 120 is not a perfect number.
Before we move on to understanding the logic of perfect numbers code-wise, we would like to know if there are infinite perfect numbers or not. To be realistic, there might be or might not be like this question is still an unsolved mystery in the world of mathematics problems. Now any of the problem solving can be done in multiple ways, and here we will look at 2 types of solutions, one being the simple one and the other being the efficient one. So, let us start with a simple solution. Intuitively one can assign a counter that will go from 1 to the one less than the number itself and check if the number is divisible by the counter. If yes, then we add it to the sum, and if not, we do nothing. At the end, we check if the sum is equal to the number, and if it is, then we return that the number is perfect; else, we return it is not. This looks like an inefficient method because if the number is huge, the time taken will also go up.
For an efficient solution, we can cut down the length the for loop has to traverse by going to the square root of the number rather than the number, and if the counter which goes from 1 to square root of the number becomes a factor, we add the number and the number which is the quotient of the number divided by the counter. In this way, we won’t have to traverse the entire length of the array and stop at just the length equal to the square root of the number.
How to Check Perfect number in Python?
In this section, we will look at the flow of the algorithm of finding the perfect number, and then an example we will look at the implementation of the flow in python.
For the simple solution:
1. Take the input number from the user.
2. Declare sum = 0;
3. Run a for loop using a temporary variable counter from 1 to the input – 1.
4. Check if the number is divisible by the counter.
5. If it divides, add the counter to the sum.
6. If it doesn’t, then do nothing.
7. Finally, out of the for loop, check if the number = sum which we obtained as a result of the earlier loop and if it is equal, return perfect number else return not a perfect number.
For the efficient solution:
1. Take the input number from the user.
2. Declare sum = 1;
3. Run a while loop using a temporary variable counter from 2 and run the loop till counter*counter <=n.
4. Check if the number is divisible by the counter.
5. If it divides, add the counter and number/counter to the sum.
6. If it doesn’t, then do nothing.
7. Increment the counter by 1.
8. Finally, out of the for loop, check if the number = sum which we obtained because of the earlier loop and if it is equal, return perfect number else return not a perfect number.
Examples
Let us discuss examples of Perfect Number in Python.
Example #1: Simple solution
Syntax
import time
def perfNumFunc(num):
sumPerf = 0
for counter in range(1, num):
if num % counter == 0:
sumPerf += counter
if(sum == num):
return "True"
else:
return "False"
begin = time.time()
print("Checking for perfect numbers:")
print("6: " + str(perfNumFunc(6)))
print("Time taken: " + str(time.time()-begin) + "s")
print("20: " + str(perfNumFunc(20)))
print("Time taken: " + str(time.time()-begin) + "s")
print("28: " + str(perfNumFunc(28)))
print("Time taken: " + str(time.time()-begin) + "s")
print("279: " + str(perfNumFunc(279)))
print("Time taken: " + str(time.time()-begin) + "s")
print("33550336: " + str(perfNumFunc(33550336)))
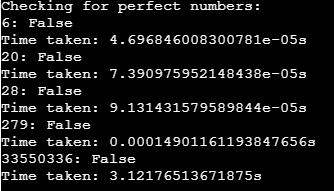
print("Time taken: " + str(time.time()-begin) + "s")Output:
Example #2: Efficient solution
Syntax:
import time
def perfNumFunc (num):
sumPerf = 1
counter = 2;
while counter * counter <= num:
if num % counter == 0:
sumPerf = sumPerf + counter + num/counter
counter += 1
if(sumPerf == num):
return "True"
else:
return "False"
begin = time.time()
print("Checking for perfect numbers:")
print("6: " + str(perfNumFunc(6)))
print("Time taken: " + str(time.time()-begin) + "s")
print("20: " + str(perfNumFunc(20)))
print("Time taken: " + str(time.time()-begin) + "s")
print("28: " + str(perfNumFunc(28)))
print("Time taken: " + str(time.time()-begin) + "s")
print("279: " + str(perfNumFunc(279)))
print("Time taken: " + str(time.time()-begin) + "s")
print("33550336: " + str(perfNumFunc(33550336)))
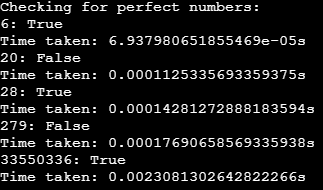
print("Time taken: " + str(time.time()-begin) + "s")Output:
Conclusion
In this article, we have gone through the methods on how can perfect number algorithm be implemented in python and look at differences in the runtime of all the cases and the visible one in the last case when the number is equal to 33550336, which clearly shows that the one we mentioned as efficient is performing efficiently!
Recommended Articles
We hope that this EDUCBA information on “Perfect Number in Python” was beneficial to you. You can view EDUCBA’s recommended articles for more information.