Updated May 8, 2023

Introduction to PostgreSQL Math Functions
The following article provides an outline of PostgreSQL Math Functions. PostgreSQL provides us with various mathematical functions to manipulate the values. The mathematical function returns us the numeric value as a result of the operation. It takes input values ( numeric ) as input which are given as arguments to the mathematical function. The functions are used to get constant values as well, like PI(3.14). There can be a mathematical function that has multiple forms with different parameters as input.
Different PostgreSQL Math Functions
Given below are different Functions:
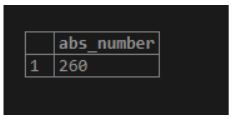
1. abs(number)
As a result, we will get the absolute value of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select abs(-260) AS abs_number;Output:
2. asin(number)
As a result, we will get the inverse sine of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT asin(1), asin(0), asin(-1), asin(sin(1)) AS inverse_sine_result;Output:
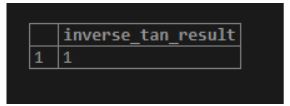
3. atan(number)
As a result, we will get the inverse tangent of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select atan(tan(1)) AS inverse_tan_result;Output:
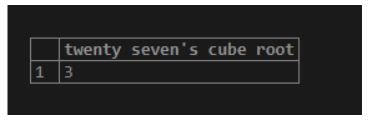
4. cbrt(number)
As a result, we will get the cube root of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT cbrt(27.0) AS "twenty seven's cube root";Output:
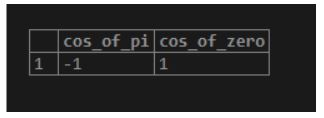
5. cos(number)
As a result, we will get the cosine of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT cos(pi()) AS cos_of_pi, cos(0) AS cos_of_zero;Output:
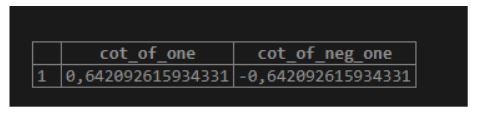
6. cot(number)
Returns the cotangent of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT cot(1) as cot_of_one, cot(-1) as cot_of_neg_one;Output:
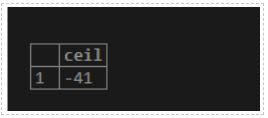
7. ceil(number)
As a result, we will get the smallest whole integer not less than a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT ceil(-41.2);Output:
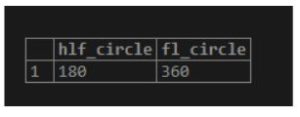
8. degrees(rad)
As a result, we will get degrees from radians rad.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT degrees(acos(-1)) AS hlf_circle, degrees(pi() * 2) AS fl_circle;Output:
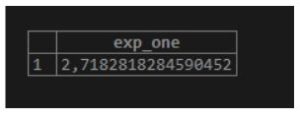
9. exp(numeric)
As a result, we will get the exponential value in the scientific notation of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT exp(1.0) AS exp_one;Output:
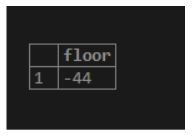
10. floor(number)
As a result, we will get the round of a number down to the nearest value, which is less than or equal to the specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select floor(-43.7);Output:
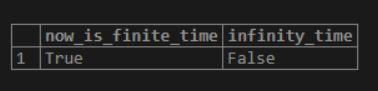
11. isfinite()
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT isfinite('now'::timestamp) AS now_is_finite_time, isfinite('infinity'::timestamp) AS infinity_time;
Output:
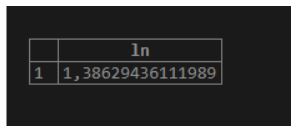
12. ln(number)
As a result, we will get the natural logarithm of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT ln(4);Output:
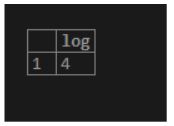
13. log(base, number)
As a result, we will get the logarithm of a specified number to a specified base.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select LOG(3, 81);Output:
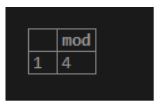
14. MOD(number1,number2)
As a result, we will divide the first number by the second number and return the remainder.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select MOD(20,8);Output:
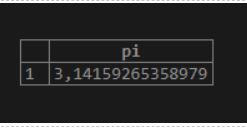
15. pi()
As a result, we will get the constant PI as (3.14159).
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select PI();Output:
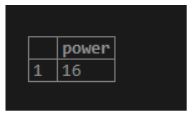
16. POWER(number1,number2)
As a result, we will raise the first number to the power of a second number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select POWER(4, 2);Output:
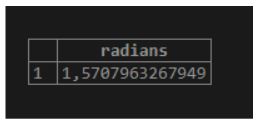
17. radians(deg)
As a result, we will get the radian value equivalent to a specified deg degree.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
select RADIANS(90);Output:
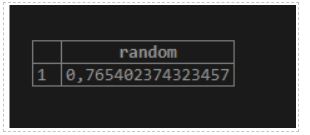
18. random()
As a result, we will get a random number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT random();Output:
19. round(number)
As a result, we will get a number rounded to the nearest whole value.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT round(2.0) AS "two",
round(2.5) AS "two point five",
round(2.6) AS "two point six",
round(2.7) AS "two point seven";Output:
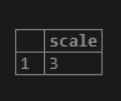
20. SCALE(number)
As a result, we will get the number of decimal digits in the fractional part.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT SCALE(2.321);Output:
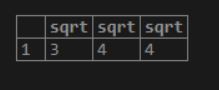
21. sqrt(number)
As a result, we will get the square root of a specified number.
Illustrate the following SQL statement and snapshot to understand the above function.
Code:
SELECT sqrt(9.0), sqrt(16.0), sqrt(pow(4.0, 2));Output:
Conclusion
From the above article, you have understood how to use the PostgreSQL mathematical functions and how the PostgreSQL mathematical functions work. Also, we have added some examples of PostgreSQL mathematical functions to understand them in detail.
Recommended Articles
We hope that this EDUCBA information on “PostgreSQL Math Functions” was beneficial to you. You can view EDUCBA’s recommended articles for more information.