Updated March 18, 2023

Introduction to Prime Number in C++
What is the prime number? Any number which is greater than 1 and it should either be divided by 1 or the number itself is called a prime number. As prime numbers cannot be divided by any other number it should only be the same number or 1. For example here is the list of Prime Number in C++ that are divisible by either 1 or number itself.
List of some Prime Numbers
2 3 5 7 11 13 17 19 23 29 31 37 41…
You might be thinking why 2 is considered as a prime number? Well, it’s an exception therefore 2 is the only prime number in the list which is also even. Only two numbers are consecutive natural numbers which are prime too! Also, 2 is the smallest prime number.
The logic behind the prime number is that if you want to find prime numbers from a list of numbers then you have to apply the mentioned below logics:
If the given number is divisible by itself or 1, 2 is the only even prime number which is an exception so always remember. Divide the given number by 2, if you get a whole number then the number can’t be prime!
Except 2 and 3 all prime numbers can be expressed in 6n+1 or 6n-1 form, n is a natural number.
There is not a single prime number that ends with 5 which is greater than 5. Because logically any number which is greater than 5 can be easily divided by 5.
For a more clear explanation that supports all the above-given logic here is the table of all the prime numbers up to 401:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 |
| 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 |
| 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 |
| 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 |
| 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 |
| 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 |
| 349 | 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 |
Prime Numbers Using Various Methods in C++
Now let’ see how to find prime numbers using various methods such as for loop, while loop, do-while loop. The output will be the same in all three loop cases because logic is the same only implementing way is different.
We will see that through a C ++ code separately for every loop.
Example #1
Finding a prime number using for loop
Code:
#include <iostream>
#include <math.h>
using namespace std;
int main() {
int x; // Declaring a variable x
cout << "Please enter the number : "; // cout to get the input value from user
cin >> x;
cout << "Here is the list of all the prime numbers Below "<< x << endl;
for ( int m=2; m<x; m++) //implementing for loop to find out prime numbers
for ( int n=2; n*n<=m; n++)
{
if ( m % n == 0)
break;
else if ( n+1 > sqrt (m)) {
cout << m << endl;
}
}
return 0;
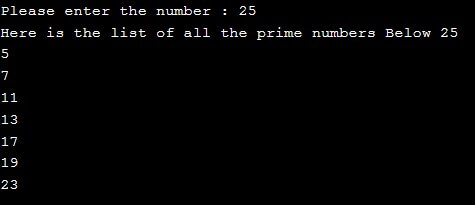
}Output:
As you can see in the above code we have taken two for loops because we need a list of prime numbers that will be below the given number in our program. We have included for loop within another for loop to make our calculation easier. A condition is added through if statement to break the loop once we reach our given number in code.
Example #2
Finding a prime number using for loop with if-else
Code:
#include <iostream>
using namespace std;
int main ()
{
int number, x, count = 0;
cout << "Please enter the number to check if it's prime or not : " << endl;
cin >> number;
if ( number == 0)
{
cout << "\n" << number << " This number is not prime";
exit(1);
}
else {
for ( x=2; x < number; x++)
if ( number % x == 0)
count++;
}
if ( count > 1)
cout << "\n" << number << " This number is not prime.";
else
cout << "\n" << number << " This is prime number.";
return 0;
}Output:
Example #3
Finding a prime number using WHILE loop with if-else
Code:
#include <iostream>
using namespace std;
int main()
{
int lower, higher, flag, temporary;
cout << "Please enter the two numbers for finding prime numbers between them: "<< endl;
cin >> lower >> higher;
if ( lower > higher) { //It will swap the numbers if lower number is greater than higher number.
temporary = lower;
lower = higher;
higher = temporary;
}
cout << "Hence the Prime numbers between the number " << lower << " and " << higher << " are: "<< endl;
while ( lower < higher)
{
flag = 0;
for ( int x = 2; x <= lower/2; ++x)
{
if ( lower % x == 0)
{
flag = 1;
break;
}
}
if ( flag == 0)
cout << lower << " ";
++lower;
}
return 0;
}Output:
In the above code, we have taken integers as a lower number, higher number, temporary variable, and a flag. Initially, we take two numbers as an input one is lower while the other is higher. In case the lower number is bigger than the higher number then these numbers will be swapped through a temporary variable first to move further in code. Now while loop will follow up until lower is less than higher and for loop, the condition will keep calculating prime numbers between them.
Conclusion
In, prime number logic can be used not only in C++ but in any programming language. From a small set of numbers to a big amount of numbers this logic can be used to find a set of prime numbers according to requirements within seconds without wasting any time in computer programming.
Recommended Articles
This is a guide to Prime Number in C++. Here we discuss the list of some prime numbers, and Various methods used for Prime Numbers. You can also go through our other suggested articles to learn more–