What is Prim’s Algorithm?
Prim’s Algorithm, an algorithm that uses the greedy approach to find the minimum spanning tree. It shares a similarity with the shortest path first algorithm. Having a small introduction about the spanning trees, Spanning trees are the subset of Graph having all vertices covered with the minimum number of possible edges. They are not cyclic and cannot be disconnected. Spanning trees doesn’t have a cycle. A connected Graph can have more than one spanning tree.
So the major approach for the prims algorithm is finding the minimum spanning tree by the shortest path first algorithm. Basically, this algorithm treats the node as a single tree and keeps adding new nodes from the Graph.
Working of Prim’s Algorithm
What Internally happens with prim’s algorithm we will check-in details:-
So it starts with an empty spanning tree, maintaining two sets of vertices, the first one that is already added with the tree and the other one yet to be included. So it considers all the edge connecting that value in MST and picks up the minimum weighted value from that edge, moving it to another endpoint for the same operation. A Cut in Graph theory is used at every step in Prim’s Algorithm, picking up the minimum weighted edges.
Pseudo Code for Prim’s Algorithm
Let us look over a pseudo code for prim’s Algorithm:-
We create two sets of vertices U and U-V, U containing the visited list and the other that isn’t. So we move the vertex from V-U to U one by one connecting the least weight edge.
- Step 1: Create two sets U and V
- Step 2: Put the start value in U from which we have to make the spanning tree.
- Step 3: While U is not equal to V, find the lowest cost to reach the edge and put that over U.
- Step 4: Repeat step 3 for other edges until an MST is achieved.
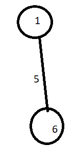
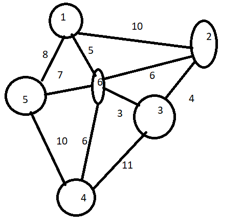
Here we can see from the image that we have a weighted graph, on which we will be applying the prism’s algorithm.
Step 1: Let us choose a vertex 1, as shown in step 1 in the above diagram. This will choose the minimum weighted vertex as prims algorithm says, and it will go to vertex 6.
The distance of other vertex from vertex 1 are 8(for vertex 5) , 5( for vertex 6 ) and 10 ( for vertex 2 ) respectively. So the minimum distance, i.e. 5 will be chosen for making the MST, and vertex 6, will be taken as consideration.
- Select vertex 6 to include in U
- Refer Step 1 in the Diagram Above.
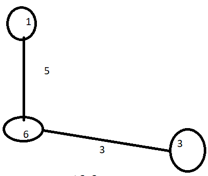
Step 2: Then the set will now move to next as in Step 2, and it will then move vertex 6 to find the same. Here it will find 3 with minimum weight so now U will be having {1,6}
Now the distance of other vertex from vertex 6 are 6(for vertex 4) , 3( for vertex 3 ) and 6( for vertex 2 ) respectively. So the minimum distance, i.e. 3 will be chosen for making the MST, and vertex 3, will be taken as consideration.
- Select vertex 3 to include in U
- Refer Step 2 in the Diagram Above.
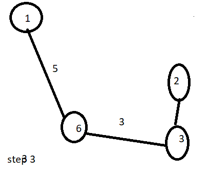
Step 3: The same repeats for vertex 3, making the value of U as {1,6,3}. Iteration 3 in the figure.
Now the distance of another vertex from vertex 3 is 11(for vertex 4), 4( for vertex 2 ) respectively. So the minimum distance, i.e. 4 will be chosen for making the MST, and vertex 2, will be taken as consideration.
- Select vertex 2 to include in U
- Refer Step 3 in the Diagram Above.
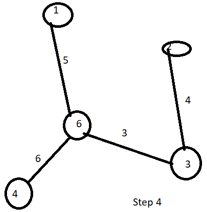
Step 4: Now it will move again to vertex 2, Step 4 as there at vertex 2 the tree can not be expanded further. So now from vertex 6, It will look for the minimum value making the value of U as {1,6,3,2}
Now the distance of other vertex from vertex 6 are 6(for vertex 4) , 7(for vertex 5), 5( for vertex 1 ), 6(for vertex 2), 3(for vertex 3) respectively. Since distance 5 and 3 are taken up to make the MST before, we will move to 6(Vertex 4), which is the minimum distance for making the spanning tree. So the minimum distance, i.e. 6 will be chosen for making the MST, and vertex 4, will be taken as consideration.
- Select vertex 4 to include in U
- Refer Step 4 in the Diagram Above.
Step 5: So in iteration 5, it goes to vertex 4, and finally the minimum spanning tree is created, making the value of U as {1,6,3,2,4}.
Now the distance of another vertex from vertex 4 is 11(for vertex 3), 10( for vertex 5 ) and 6(for vertex 6) respectively. Since 6 is considered above in step 4 for making MST. So 10 will be taken as the minimum distance for consideration. So the minimum distance, i.e. 10, will be chosen for making the MST, and vertex 5, will be taken as consideration.
- Select vertex 5 to include in U
- Refer Step 5 in the Diagram Above.
- Now again in step 5, it will go to 5 making the MST.
All the vertices are included in the MST to complete the spanning tree with the prims algorithm. Now ,cost of Minimum Spanning tree = Sum of all edge weights = 5+3+4+6+10= 28
Time Complexity Analysis
Worst Case Time Complexity for Prim’s Algorithm is: –
- O(ElogV) using binary Heap
- O(E+VlogV) using Fibonacci Heap
All the vertices are needed to be traversed using Breadth-first Search, and then it will be traversed O(V+E) times. Min heap operation is used that decided the minimum element value taking of O(logV) time. So the merger of both will give the time complexity as O(Elogv) as the time complexity.
Conclusion
So from the above article, we checked how prims algorithm uses the GReddy approach to create the minimum spanning tree. The use of greedy’s algorithm makes it easier for choosing the edge with minimum weight. Also, we analyzed how the min-heap is chosen, and the tree is formed. The time complexity for this algorithm has also been discussed, and how this algorithm is achieved we saw that too. by this, we can say that the prims algorithm is a good greedy approach to find the minimum spanning tree.
Recommended Articles
This is a guide to Prim’s Algorithm. Here we discuss what internally happens with prim’s algorithm we will check-in details and how to apply. You can also go through our other related articles to learn more –