Updated March 31, 2023

Introduction to Priority queue algorithm
Priority Queue is the modified version of queues in which each element will have a priority value, and operations on elements are performed based on their priority. Generally, The numbers with the highest value are deleted first than the elements with the lowest value.
Difference between Queue and Priority Queue
Let us define the differences between Queue and Priority Queue using an example.
If you stand in a queue to buy a movie ticket, the person who stands first gets the first ticket and will be the first person getting out of the Queue. This is an example of a Normal-Queue, that follows the FIFO principle that is ‘First In First Out. But, That is not the case in a hospital where patients with critical conditions will be treated first and then the patients with Normal conditions. This is known as the priority queue. The same principles apply to the numbers queue.
The number with the highest priority will be deleted first, followed by the second, third priority numbers, and vice versa.
Working of Priority Queue
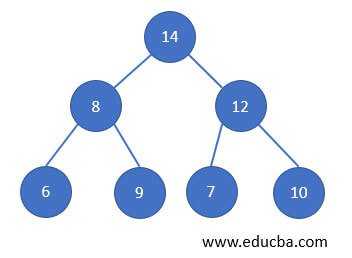
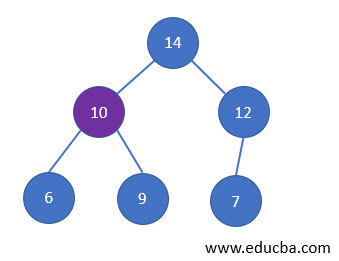
Before writing an algorithm, let us see the working principle of Priority Queue with an example.
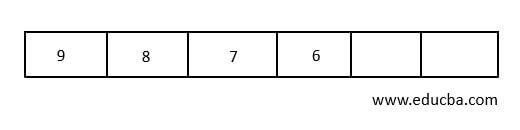
- Lets us take an empty Queue
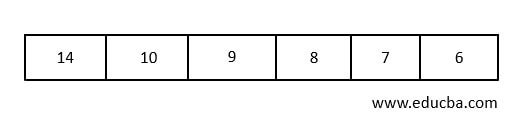
- Insert numbers in the Queue from one end.
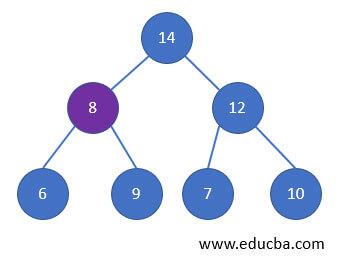
- To DeQueue elements in Priority Queue, values with the highest priority are to be deleted first. Mainly, we can set the highest value as the priority. The element with the highest value can be considered as the highest priority element, and also the element with the lowest value can be considered as the highest priority. According to our priority element, the DeQueue process is initiated. To DeQueue an element, the element with the highest priority is to be checked first, and then it is deleted.
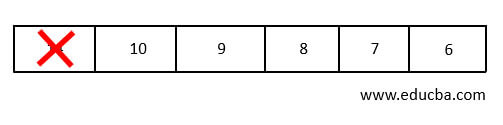
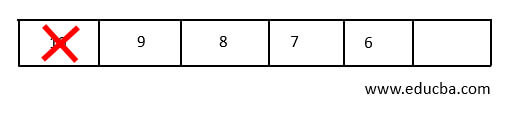
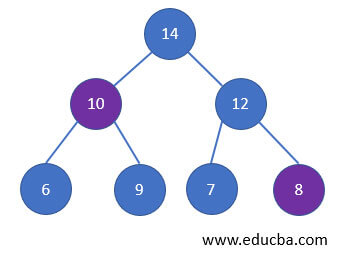
- Let us consider the highest value as our priority element, then the first element that is deleted from the queue will be 14.
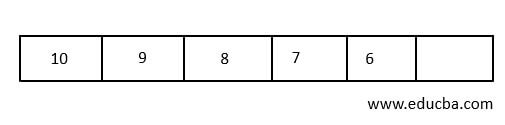
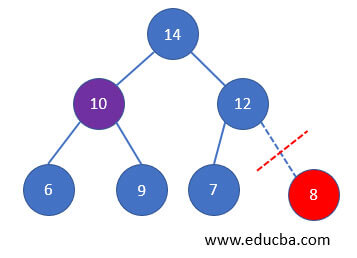
- Since the second highest element is 10. It will get deleted after 14.
- In the same way, according to the priority, all elements get deleted in the Queue.
Priority Queue Implementation
A better implementation of Priority Queue is to use Binary Heap. Although there are many ways to implement Priority Queue like using arrays, linked lists, or binary search tree, Binary Heap data structure is an efficient way to implement Priority Queue.
Basic operations of Priority Queue include Insertion and Deletion.
Let us understand this using an example
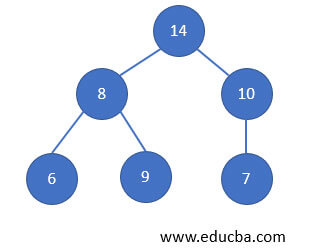
Inserting an element into the Priority Queue
- Implement binary heap to the above example.
- Insert a new element at the end of the tree.
- Heapify the tree to get a binary heap
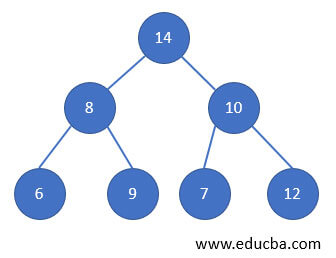
Deleting an element from the Priority Queue
- Deleting an element from the max-heap is done as given below.
Select an element to be deleted
- Swap it with the last element of the Binary Heap.
- Now remove the last element of the heap
- Heapify the new Binary heap tree
Algorithm for implementing Priority Queue using Binary Heap
Step1: Create a function heapify() to heapify the elements in the Binary Tree if any changes are made.
Step2: Find the largest among root, left child, and right child, then recursively call the same function until the root element matches the largest element.
Step3: Create a function insert() to insert an element into the tree, which takes an array and the number which is to be inserted as input.
Step 4: If the size of the array is zero, then this number will be the root, else append the number and call the heapify function recursively to heapify the elements.
Step5: Create a function deleteNode() that deletes the selected element from the tree
Step 6: Delete the element and again heapify the elements recursively.
Step 7: Insert elements into an empty array using the insert() function then try deleting an element from the tree.
Example
Source Code for Priority Queue using Heap in Python
# Priority Queue implementation in Python
# Function to heapify the Binary tree
def heapify(arr, n, i):
# Find the largest among the root, left child and right child
largest = i
l = 2 * i + 1
r = 2 * i + 2
if l<n and arr[i] < arr[l]:
largest = l
if r<n and arr[largest] < arr[r]:
largest = r
# Swap and continue heapifying if the root is not largest
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
# Function to insert an element into the tree
def insert(array, newNum):
size = len(array)
if size == 0:
array.append(newNum)
for i in range((size // 2) - 1, -1, -1):
heapify(array, size, i)
# Function to delete an element from the tree
def deleteNode(array, num):
size = len(array)
i = 0
for i in range(0, size):
if num == array[i]:
break
array[i], array[size - 1] = array[size - 1], array[i]
array.remove(size - 1)
for i in range((len(array) // 2) - 1, -1, -1):
heapify(array, len(array), i)
arr = []
insert(arr, 3)
insert(arr, 4)
insert(arr, 9)
insert(arr, 5)
insert(arr, 2)
#Print the Max Heap
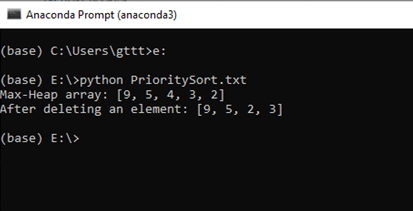
print ("The Max-Heap array is: " + str(arr))
#Print the final heap after deleting an element
deleteNode(arr, 4)
print("After deleting an element: " + str(arr))
Output:
Applications of Priority Sort
- Priority Queue Algorithm can be used to balance the load in operating systems.
- This Queue can also be used for implementing stacks in data structures.
- By using Binary Heap, Priority Queue can be used in the most popular Graph algorithms like Dijkstra’s for finding the shortest path, Prim’s Minimum Spanning tree, etc.
- All the Queue applications where priority is involved.
Conclusion
- Priority Queue is the extended version of queues in which each element will have a priority value, and operations on elements are performed based on their priority.
- Queue follows the principle of First-in First-out but Priority Queue performs functions according to the Priority of the elements.
- The best way to implement Priority Queue is by using Heaps.
- Priority Queue Algorithm can be used in balancing the load, in stacks, and in Dijkstra’s algorithm for finding the shortest distance.
Recommended Articles
This is a guide to Priority queue algorithm. Here we discuss the Algorithm for implementing Priority Queue using Binary Heap. You may also have a look at the following articles to learn more –