Python Math Floor Function
In Python, the math module provides a range of functions for various mathematical computations. There is a floor() function in the math module, which is used to take the nearest integer that is either less than or equal to the given number. The floor() function truncates the number and rounds it down to the nearest integer.
In Math and Computer Science, the floor function provides the smallest integer for non-integer double and float values. For example, if we have 8/3, resulting in 2.6667, applying the floor function gives us 2.
Table of Contents
Syntax of Python Math Floor Function
There are two ways to work with floor() functions in Python.
In the first method, you can simply import math class, and then you can use the floor() function. The syntax is given below:
import math
math.floor(8.75)The output will be 8.
In the second method, you can simply import Math, and then you can use the math.floor() function. The syntax is given below:
from math import floor
floor(8.75)The output will be 8.
The math.floor function takes a number (positive/negative float or integer) as a parameter. It returns an integer (no more than n for float, same for integer).
It does not take infinity and strings as parameters. If you give infinity and string as parameters, it will throw an error.
The floor function rounds down positive and negative numbers. It always yields a result less than or equal to the original value. For example,
import math
result_positive = math.floor(8.75)
result_negative = math.floor(-4.25)
print(result_positive)
print(result_negative)Output:
Note that 8.75 is a positive number, and its lowest integer is 8. Similarly, -4.25 is a negative number; its lowest integer is -5.
Exceptions of Python Math Floor Function
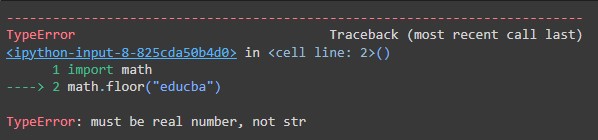
There are some exceptions in floor function. For example, if you pass a string instead of a number to the floor function, then it will throw a TypeError:
import math
math.floor("educba")Output:
It will throw this error:
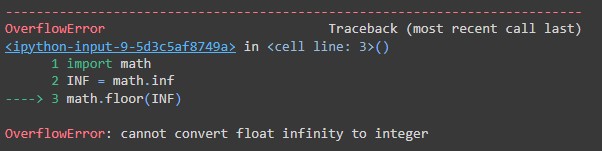
You will get an OverflowError if you try to convert an infinite value to a floor value. For example,
import math
INF = math.inf
math.floor(INF)Output:
It will throw this error:
The round() and floor() function
from math import floor
# floor function examples
result1 = floor(18.789)
print(result1)Output
result2 = floor(145.678)
print(result2)Output
result3 = floor(-112.345)
print(result3)Output
result4 = floor(-129.876)
print(result4)Output
result5 = floor(67.89)
print(result5)Output
# round function examples
result6 = round(18.789)
print(result6)Output
result7 = round(145.678)
print(result7)Output
result8 = round(-112.345)
print(result8)Output
result9 = round(-129.876)
print(result9)Output
Similarly, you can use the int() function, which truncates the given float number. You can see the difference when you use negative numbers.
Rounding down goes away from 0. At the same time, trunking goes closer to 0. Therefore, floor() is always less than or equal to, and int() is close to zero or equal.
For example,
from math import floor
# floor function examples
result1 = floor(18.789)
print(result1)Output:
result2 = floor(145.678)
print(result2)Output:
result3 = floor(-112.345)
print(result3)Output:
result4 = floor(-129.876)
print(result4)Output:
result5 = floor(67.89)
print(result5)Output:
# int function examples
result10 = int(25.678)
print(result10)Output:
result11 = int(189.456)
print(result11)Output:
result12 = int(-123.789)
print(result12)Output:
result13 = int(-157.345)
print(result13)Output:
result14 = int(90.123)
print(result14)Output:
These are comparisons between the floor (), round(), and int() Python functions
| Function | Purpose | Example | Result |
| floor() | Rounds down to the nearest integer | math.floor(5.8) | 5 |
| round() | Rounds to the nearest integer, with ties rounding to the nearest even integer (bankers’ rounding by default) | round(5.8) | 6 |
| int() | Truncates decimal part, effectively rounding towards zero | int(5.8) | 5 |
Usages of floor() function
You can use floor() functions in finance, data analysis, and computer science. For examples,
In finance, you can figure out the smallest monthly mortgage payment using interest rates and how long you will have the loan.
from math import floor
# Finance Example: Calculate the smallest monthly mortgage payment
interest_rate = 0.03
loan_duration_years = 30
loan_amount = 100000
monthly_payment = floor(loan_amount * (interest_rate * (1 + interest_rate) ** loan_duration_years) /
((1 + interest_rate) ** loan_duration_years - 1))
print("Smallest Monthly Mortgage Payment:", monthly_payment)Output:
You can simplify continuous numbers by breaking them into groups for data analysis. So it will be easier to understand and study.
from math import floor
# Data Analysis Example: Discretize continuous numbers
continuous_numbers = [15.7, 24.3, 38.2, 49.8, 62.1]
discretized_numbers = [floor(num) for num in continuous_numbers]
print("Discretized Numbers:", discretized_numbers)Output:
In computer science, you can use the floor() function to divide and share resources among different program parts.
from math import floor
# Computer Science Example: Divide and share resources
total_resources = 100
parts = 5
resources_per_part = floor(total_resources / parts)
print("Resources per Part:", resources_per_part)Output:
Behavior of floor() function
You can explore how the floor function behaves, addressing positive and negative numbers, fractions, and specific cases.
It consistently rounds down, even for negative values. For example, floor(-6.2) returns -7.
from math import floor
# Rounding down for negative values
result1 = floor(-6.2)
print(result1)Output:
Fractions are always rounded down to the closest integer. For example, both floor(8.6) and floor(4.3) return 8 and 4 respectively.
from math import floor
# Rounding down fractions to the closest integer
result2 = floor(8.6)
print(result2)Output:
result3 = floor(4.3)
print(result3)Output:
When the input is already an integer, it provides the same result. For example, floor(12) returns 12.
from math import floor
# When the input is already an integer
result4 = floor(12)
print(result4)Output:
Common pitfalls and mistakes to avoid while using the floor() function
There are various common pitfalls and mistakes while using the floor() function in Python programs. Some of them are discussed here.
1. Not importing the floor function
When you use the floor in your Python code, then you must import the floor function from the math module.
Mistake:
# Incorrect
result = math.floor(8.5)Correct:
# Correct
from math import floor
result = floor(8.5)You can use the floor in your code when you import the floor.
2. Not handling Input type
You should be aware of input type while working with floor function. For example,
Mistake:
# Incorrect
value = input("Enter a number: ")
result = floor(value)Correct:
# Correct
value = float(input("Enter a number: "))
result = floor(value)You should specify the type of input here, which should be float.
3. Ignoring Exception Handling
You should handle exceptions properly when working with floor functions in Python programs. For example,
Mistake:
# Incorrect
value = "Invalid"
result = floor(value)Correct:
# Correct
try:
value = float("Invalid")
result = floor(value)
except ValueError as e:
print("Error:", e)The incorrect example does not handle the case where the input cannot be converted to a float. The correction uses a try-except block to catch and handle a ValueError if the conversion fails.
4. Not applying floor() function to individual elements in a List
You should use the floor() function to individual elements in a List. For example,
Mistake:
# Incorrect
numbers = [5.7, 8.2, 4.9]
rounded_numbers = floor(numbers)Correct:
# Correct
numbers = [5.7, 8.2, 4.9]
rounded_numbers = [floor(num) for num in numbers]The incorrect example attempts to apply the floor() function to a list directly, which is invalid. The correction uses a list comprehension to apply the floor() function to each element in the list individually.
5. Floating-point precision
Floating-point precision can lead to unexpected results. So, you should be careful in certain scenarios. For example,
result = math.floor(0.1 + 0.2)Output:
The floor() and ceil() function in Python
The closest integer is rounded up by the ceil() function. For example, when applied to the number 4.5, it will return 5.
The floor() function finds the nearest integer by rounding down For example, when applied to the number 4.5, it will return 4.
| Section | Floor Function | Ceil Function |
| Rounding Direction | Rounds down to the nearest integer | Rounds up to the nearest integer |
| Example | floor(3.5) = 3 | ceil(3.5) = 4 |
| Example | floor(7.2) = 7 | ceil(7.2) = 8 |
| Example | floor(-4.8) = -5 | ceil(-4.8) = -4 |
| Use Case | Useful when values need to be rounded down, like counting whole units | Handy when rounding up is required, such as allocating resources or determining minimum elements |
| Application Scenario | Determining the number of whole units | Allocating resources or ensuring a minimum quantity |
Distinction from round()
While the round() function follows traditional rounding, the floor function strictly rounds down. For example,
rounded_value = round(8.75)
print(rounded_value)Output:
floored_value = math.floor(8.75)
print(floored_value)Output:
Differences from ceil()
The math. ceil() function always rounds up, the floor function ensures a rounded-down result. For example,
ceiled_value = math.ceil(8.75)
print(ceiled_value)Output:
floored_value = math.floor(8.75)
print(floored_value) Output:
Conclusion
In Python, two Math modules for rounding fractional numbers are floor() and ceil(). For round numbers, the math floor() function is useful. You need to import the floor function from the math module to use it. The floor function works on positive/negative numbers and integers. Its output is a number not exceeding the specified value of ‘n.’ Floor() in Python is valuable for rounding down real numbers. It is beneficial for math tasks in data science and other applications. But you should be aware of potential errors and mistakes while using it.
Python’s helpful tool for rounding down is the math.floor() function.non-integer floats and double values to the nearest integer. It is used in various fields like finance, data analysis, and computer science.
FAQs (Frequently Asked Questions)
Q1. Can the math.floor() function be used with complex numbers in Python?
Answer: No. The math.floor() function is designed for real numbers. But if you try to use it with complex numbers, it will result in TypeError.
Q2. Is there a limit to the size of the numbers that the math.floor() function can handle?
Answer: The math.floor() function can handle a wide range of numeric values. But if very large and very small numbers are used. Then, there might be limitations due to floating-point precision. You should be aware of such cases.
Q3. How does the performance of the math.floor() function compare to alternative rounding methods for large datasets?
Answer: While the math.floor() function is generally efficient. Still, the outcome may differ depending on the size of the dataset. In some cases, alternative rounding methods and optimizations might be considered for large-scale applications.
Q4. Can the math.floor() function be used with NumPy arrays for efficient element-wise operations?
Answer: Yes. The math.floor() function can be applied to NumPy arrays using vectorized operations for efficient element-wise rounding. This approach is more efficient than applying the function to each element individually in a loop.
Recommend
We hope that this EDUCBA information on “Python Floor Function” was beneficial to you. You can view EDUCBA’s recommended articles for more information.
Python float to int
pop() in Python
Python YAML Parser
Python ceil() Function