Introduction to Python Modulo Operator
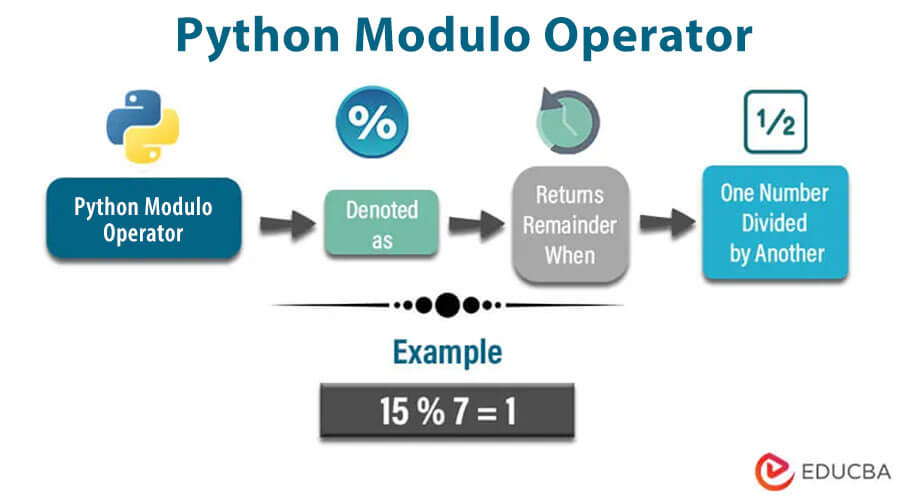
The Modulo operator in Python (denoted by the symbol “%”) is a fundamental arithmetic operator that calculates the remainder of the division of two numbers. The Modulo operator determines what is left over when dividing one number by another. The Modulo operator is commonly used in various programming tasks, including checking for even or odd numbers, cycling through a range of values, and more.
Table of Content
- Introduction to Python Modulo Operator
- Key takeaway
- Importance of Modulo Operator in Programming
- Difference between Division and Modulo Operators
- Examples of Python Modulo Operators
- Tips for Optimizing Modulo-related Operations
- Common Mistakes and Misconceptions of the Python Modulo Operator
Key takeaway
- When dividing one integer by another, you can use the Python Modulo operator (“%”) to calculate the remainder.
- This operator returns an integer result and helps determine whether a number is even or odd, handling cyclic patterns and performing various mathematical tasks.
- Knowing potential division by zero scenarios and understanding the sign rules is essential to avoid common pitfalls.
Syntax:
x % yDividend % Divisor: The remainder is obtained when x is divided by y. The remainder will be an integer if both dividends are integers. The remainder will be a floating-point number if one among dividends or divisors is a float number.
For example, if we execute the operation 10% 3, the modulo operator will calculate the remainder of dividing 10 by 3, which is 1. As a consequence of this process, the outcome would be 1.
Importance of Modulo Operator in Programming
The modulo operator is used in a variety of tasks and algorithms. You can use the module or ask for Python homework help if you need it to complete your programming tasks.Some of the primary reasons for its importance are as follows:
Identifying even and odd numbers: Using the modulo operator on a number, we may quickly tell if it is even or odd. When dividing by 2, even numbers always result in a remainder of 0, while odd numbers have a remainder of 1.
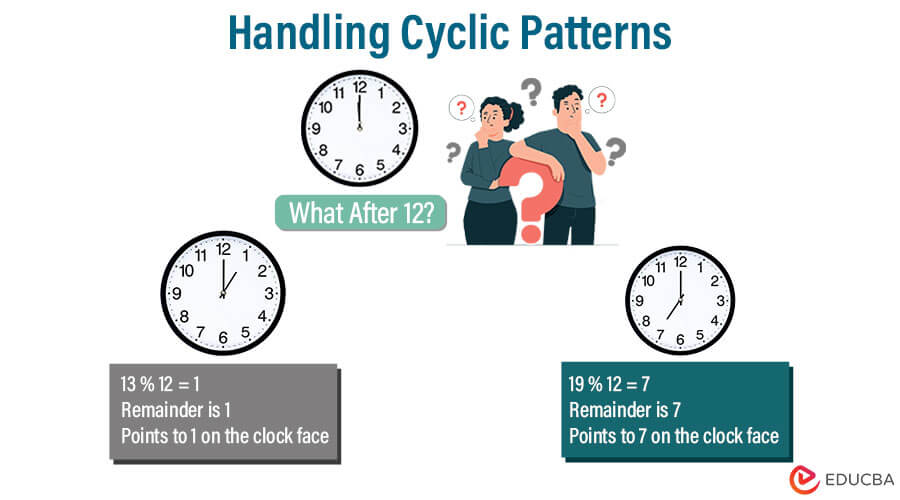
Handling cyclic patterns: The modulo operator is essential in various applications, including creating circular data structures like circular lists or queues, generating animations, and simulating periodic behavior. It wraps around values within a predetermined range.
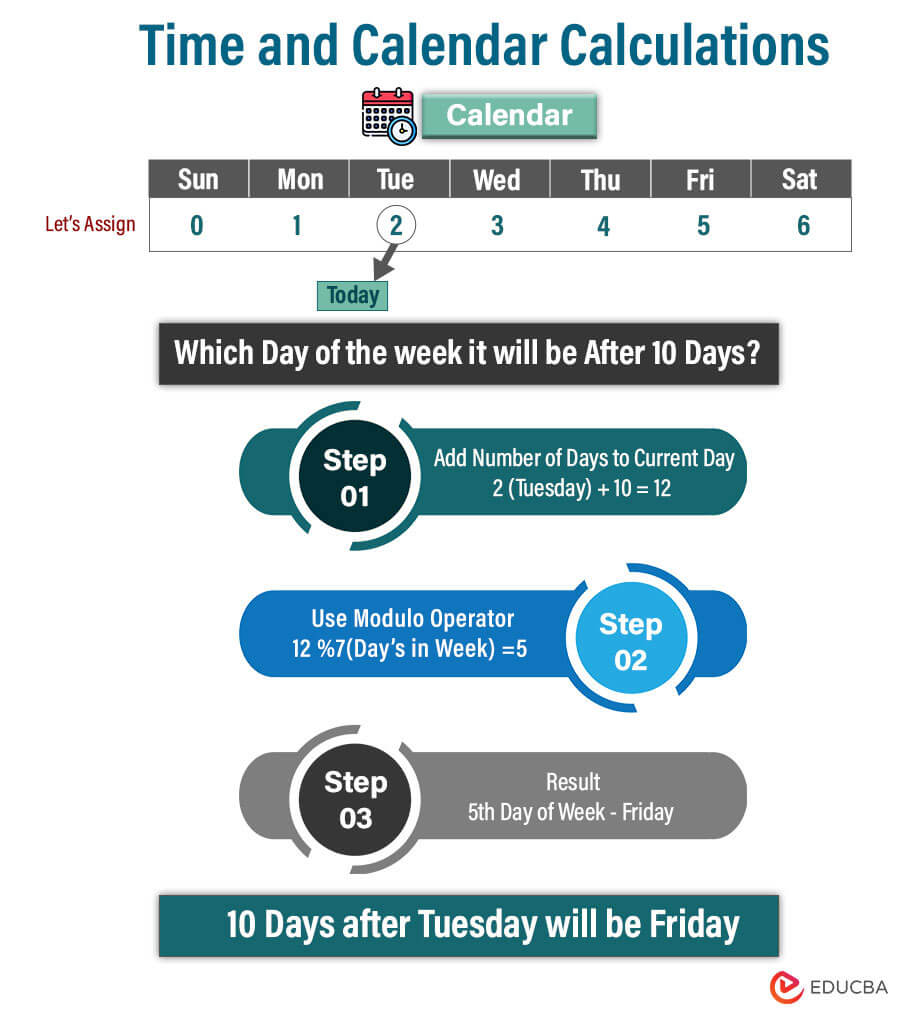
Time and calendar calculations: The modulo operator can simplify time and date calculations, such as determining the day of the week or detecting leap years.
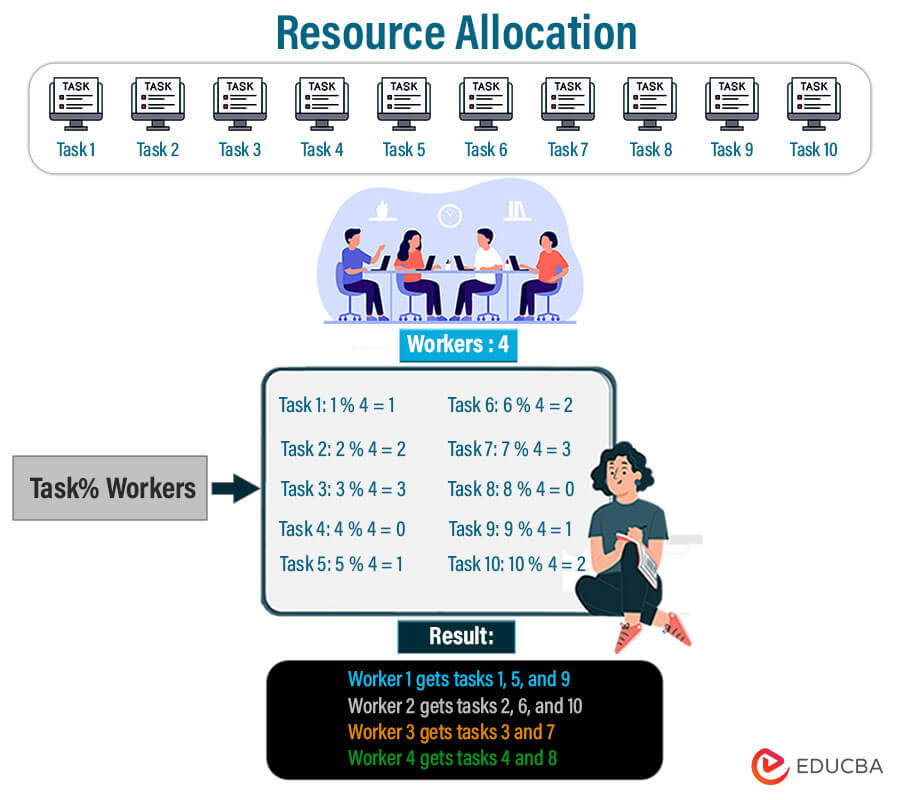
Resource Allocation: When resource allocation involves dividing jobs among workers or resources among processes, the modulo operator is useful for load balancing and equitably distributing duties.
Difference between Division and Modulo Operators
The division operator (/) and the modulo operator (%) both conduct division-related operations, although they serve different functionalities:
Division (/): The division operator divides two numbers usually and returns the result as a floating-point number, even if the operands are integers. For example, 10 / 3 would result in 3.3333333333333335.
Modulo (%): The modulo operator, also called a remainder operator, computes the remaining value after dividing one number by another. It returns the remainder as an integer value. For example, 10 % 3 would result in 1.
The division operator is essential for obtaining exact fractional results, but the Modulo operator is beneficial for tasks such as detecting even or odd integers, implementing cyclic behavior, and dealing with cyclical data structures.
Examples of Python Modulo Operators
Following are the different examples of Python Modulo Operators.
Example #1
Code:
x = 5
y = 2
r = x % y
print ('Remainder is:', r)Output:
Explanation: In the above example, x = 5 , y =2, so 5 % 2 , 2 goes into 5 twice, yielding 4, so the remainder is 5 – 4 = 1. To obtain the remainder in Python, you can use the numpy.remainder() function found in the numpy package. It returns the remainder of the division of two arrays and returns 0 if the divisor array is 0 (zero) or if both arrays have an array of integers. This function is also used on individual numbers.
Example #2
Code:
import numpy as np
n1 = 6
n2 = 4
r = np.remainder(n1, n2)
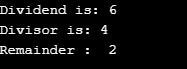
print ("Dividend is:", n1)
print ("Divisor is:", n2)
print ("Remainder : ", r)Output:
Explanation: The above example uses numpy.remainder() function on the given dividend and divisor to find the remains of two, which works similarly to the modular operator. In this example, it is 6 % 4, 4 goes into 6, one time which yields 4, so the remainder is 6 – 4 =2.
Example #3
Code:
import numpy as np
arr1 = np.array([7, -6, 9])
arr2 = np.array([3, 4, 3])
rem_arr = np.remainder(arr1, arr2)
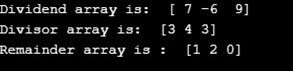
print ("Dividend array is: ", arr1)
print ("Divisor array is: ", arr2)
print ("Remainder array is : ", rem_arr)Output:
Explanation: To calculate the remainder of each item in a list or array, use the numpy.remainder() function as demonstrated in the example above. We have two arrays [7 -6 9] and [3 4 3], so 7 % 3,3 goes into 7 two times, so the remainder is 1, -6 % 4, 4 goes into 6 one time, so the remainder is 2, 9 % 3, 3 goes into 9 three times, so the remainder is 0. The array of remainder values will be [1 2 0].
Example #4
To determine whether a number is even or odd, you can use a modulo operator. Below is a code to print odd numbers between 0 and 20.
Code:
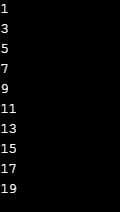
for num in range(1, 20):
if(num % 2 != 0):
print(num)Output:
Explanation: In the above example, a modulo operator prints odd numbers between 0 and 20 from the code; when a number can be divided by 2, and the remainder is 0, we classify it as an even number; otherwise, it’s an odd number.
If the number is 2, then 2 % 2 gives remainder 0, so it’s an even number, not odd, now; if the number is 3, then 3 % 2 gives remainder 1, which 2 goes into 3 one time, so yields 2 and remainder is 3 – 2 =1 which not zero. Hence, the given number 3 is odd, and using a for loop, it will check till 20 numbers and print all the odd numbers between 0 and 20. You can use the Modulo on floating-point numbers, unlike the division operator (//), which only works on integers and provides the remainder in integer form.
Example #5
Code:
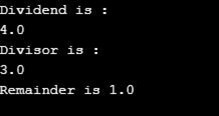
a = input("Dividend is :\n")
fa = float(a)
b = input("Divisor is :\n")
fb = float(b)
fr = fa % fb
print ("Remainder is",fr)Output:
Explanation: In the above example, the user enters the dividend and divisor into input() to calculate the remainder of a division. After converting the values to floating-point numbers, the code calculates the remainder using the modulus operator “%”. The calculated remainder is displayed using print().
Example #6
The modulo operator in Python also works on negative numbers and gives the same remainder as positive ones. However, the negative sign of the divisor will remain in the remainder.
Code:
print(-5 % 3)Output:
Code:
print(5 % -3)Output:
Logic Behind the Code:
-5 % 3 = (1 -2*3) % 3 = 1
5 % -3 = (-1 * -2*-3) % 3 = -1Explanation: These negative numbers use the fmod() function to find the remainder; we can use the fmod() function of the math library when either the dividend or the divisor is negative. Additionally, this function can be used to find the remainder of floating-point numbers.
Example #7
Code:
import math
a = -10
b = 3
print(math.fmod(a,b))Output:
Explanation: In Python, the modulo operator gives an error when the divisor is zero (0). We typically encounter a ZeroDivisionError when attempting to divide any number by zero, resulting in an answer of infinity (∞).
Example #8
Code:
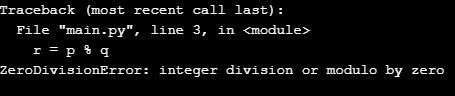
p = 10
q = 0
r = p % q
print(r)The above code gives us an error, as shown in the below screenshot.
Output:
Code:
p = 10
q = 0
try:
rem = p % q
print(rem)
except ZeroDivisionError as zde:
print("Cannot divided by 0",)You can utilize try-except blocks to catch this error. Refer to the screenshot provided below for an example.
Output:
Example #9
Code:
year = 2023
if year % 4 == 0 and (year % 100 != 0 or year % 400 == 0):
print(f"{year} is a leap year.")
else:
print(f"{year} is not a leap year.")Output:
Explanation: We utilize the modulo operator in this example to check for leap years. A leap year is a year that can be divided evenly by 4, except for years that are divisible by 100 but not by 400. The result for the year = 2023 will be “2023 is not a leap year.”
Tips for Optimizing Modulo-related Operations
- Use Bitwise AND for Powers of Two: To obtain the remainder of division by a power of two (e.g., 2, 4, 8, 16), use bitwise AND instead of the modulo operator for better efficiency. For example, to find the remainder of num divided by 8, remainder = num & 7. This works because 7 in binary is 0111, and bitwise AND with 0111 effectively lowers the value to its three least significant bits, which is the remainder when dividing by 8.
- Minimize the Use of Division: Division operations may be costly in terms of computation. If you require the remainder of a division, skip the division and use the modulo operator. Reducing the number of divisions can boost performance dramatically.
- Use Caching for Repeated Computations: Consider caching to retain the results and avoid unnecessary computations if you frequently compute the remainder for the same divisor. Caching can be extremely useful when working with large numbers or using the modulo operator in loops.
- Consider Using Integer Division Instead: Consider utilizing integer division (//) instead of performing separate division and remainder operations if you require both the quotient and the remainder of a division. This enables you to achieve both outcomes in a single operation, potentially enhancing performance.
- Avoid Unnecessary Conversions: Take note of data types and conversions. Conversions between various data types that are not required might create overhead. Instead of first converting floating-point values to integers, use the modulo operator directly on integers.
- Avoid Redundant Operations: Examine your code for any redundant or needless activities that might be eliminated. The execution time can be optimized by simplifying expressions and removing redundant calculations.
- Profile Your Code: Use profiling tools to find performance bottlenecks in your code. This assists you in identifying areas where the remaining operator or associated activities may substantially affect performance.
- Use Built-in Functions for Common Operations: Python has built-in functions for performing particular remainder-related operations. Divmod(), for example, returns both the quotient and the remainder of a division. Use these built-in functions when applicable, as they are frequently optimized for efficiency.
- Leverage Python Libraries: Some specialized libraries, such as NumPy, may have optimized functions for modulo operations. Consider utilizing these libraries to increase speed when dealing with large arrays or complicated computations.
- Choose the Right Algorithm: More effective algorithms or mathematical tricks may be available for specific mathematical tasks involving remainders. Find the best algorithm for your particular use case by doing some research.
Common Mistakes and Misconceptions of the Python Modulo Operator
- Confusing Division and Modulo Operators: When trying to find the remainder of a division operation, use the division operator (“/”) rather than the modulo operator (“%”).
- Misunderstanding Floor Division: Confusion between the floor division operator (“//”) with the modulo operator (“%”) causes inaccurate results.
- Mishandling Negative Numbers: Assuming that the modulo operator with negative numbers always produces a positive result.
- Incorrect Use with Floating-Point Numbers: Because of floating-point precision difficulties, expect exact results when using the modulo operator with floating-point values.
- Not Handling Division by Zero: Using the modulo operator to divide by zero, resulting in a ZeroDivisionError.
- Not Considering Sign Rules: Not understanding how the sign of the result is affected by the sign of the dividend and divisor.
- Using the Modulo Operator for Non-Numeric Data: Attempting to use the remainder operator to non-numeric data types results in a TypeError.
- Incorrect Use in Complex Expressions: Using the modulo operator within complex expressions without taking operator precedence and order of operations into account.
- Overlooking Priority of Parentheses: When combining the modulo operator with other arithmetic operators, do not use parentheses to control the order of operations.
- Assuming Commutativity: Assuming that the modulo operator is commutative means that the order of the operands is irrelevant. However, it affects the result, especially with negative numbers.
Conclusion
The Python modulo operator (“%”) is a vital arithmetic operator used to determine the remainder when one integer is divided by another. It is a flexible operator with several programming uses, ranging from detecting even or odd integers to dealing with cyclic data structures and executing specific mathematical algorithms. Programmers may leverage their power and improve the robustness and efficiency of their Python programs by knowing their features, avoiding frequent errors, and utilizing them wisely.
FAQs (Frequently Ask Question)
1. Is the modulo operator commutative?
Answer: No, the modulo operator is not commutative. The order of the operands affects the result, especially when working with negative numbers.
2. Can the modulo operator be used in cryptographic algorithms or hashing functions?
Answer: Yes, the modulo operator may be employed to transform data and achieve desirable security properties in some cryptographic algorithms and hashing functions.
3. Does the locale or regional settings affect the Python modulo operator?
Answer: No, the locale or regional settings do not affect the Python modulo operator. It only works with numbers and adheres to standard arithmetic rules.
Recommended Articles:
We hope that this EDUCBA information on “Python modulo Operator” benefited you. You can view EDUCBA’s recommended articles for more information,