Updated December 26, 2023
Introduction of RSA Algorithm
The RSA (Rivest-Shamir-Adleman) algorithm plays a widespread role in securing data transmission and serves as a public-key cryptographic algorithm. The security of RSA largely depends on the difficulty of factoring large numbers. RSA does not typically earn the label of being “highly quick.” It operates at a slower pace compared to symmetric key algorithms. It often finds use in encrypting small amounts of data, such as symmetric keys used for encrypting larger data blocks.
Table of Contents
- Introduction of RSA Algorithm
- What are Public and private key Cryptography?
- How to generate public & private keys in C
- Working of RSA Algorithm in C
- Method and Approaches
- Examples a program in C
- Advantages
- Disadvantages
The fundamental operations in RSA are encryption and decryption, based on a pair of keys: a public key and a private key. In C programming, implementing RSA involves understanding both the mathematical concepts behind the algorithm and the nuances of the C language. Here’s an introduction to implementing the RSA algorithm in C:
Understanding RSA Key Generation
1. Selection of Prime Numbers (p and q):
- RSA begins with selecting two large prime numbers, denoted as p and q. These primes are kept secret.
- The selection of large and random prime numbers ensures the algorithm’s security, as the difficulty of breaking RSA encryption is based on the challenge of factoring the product of two large primes.
2. Calculation of n (n = p * q):
- The next step is calculating n, which is the product of p and q (n = p * q).
- The number ‘n’ functions as the modulus for both the public and private keys, and it is a component present in the public key.
3. Calculation of the Totient Function (φ(n)):
- The totient function, denoted as φ(n), is calculated as (p – 1) * (q – 1).
- φ(n) represents the count of numbers less than n that are coprime to n. In the context of RSA, it ensures that the chosen e (part of the public key) and d (part of the private key) function correctly for the encryption and decryption processes.
4. Selection of e (the Public Key Exponent):
- e is chosen as a substantially prime integer to n and falls within the 1 < e < φ(n)
- Additionally, e must be coprime to φ(n), which means e and φ(n) should have no common factors other than 1.
- Commonly, values like 3, 5, or 65537 are used as e due to their properties that make computations efficient.
Why These Steps are Important:
- Security: The security of RSA relies on the fact that while it’s easy to multiply p and q to get n, it’s extremely difficult to go the other way—deriving p and q from n (known as factoring) when p and q are large primes.
- Encryption & Decryption: The public key (made of n and e) is used for encrypting messages, while the private key (involving n and d, where d is calculated based on e and φ(n)) is used for decrypting them. These keys possess mathematical properties that guarantee only the corresponding private key can decrypt a message encrypted with the public key.
Key takeaways
- Enhance the security with separate public and private keys.
- RSA algorithm provides authentic Data transmission.
- People widely use them to secure communication protocols, VPNs, and digital signatures.
- RSA technique exchanges secret keys without actually sending them through the network.
- You can use it with another encrypting method to enhance security.
What are Public and private key Cryptography?
To understand public and private keys, let us briefly learn what cryptography is and its working system. Cryptography secures communication and information by encoding them before sending them. It uses a pair of keys, the public key, and its corresponding private key.
The owner creates these two keys. The owner distributes the public key openly so users can use it to send encrypted messages. The Owner has the corresponding private key and uses this key to decrypt the received encrypted message.
- The public key and the private are mathematically related to each other.
- The private key cannot be derived from its corresponding public key even though they are related.
- The owner possesses the private key, which is not openly distributed.
- You cannot use the public key to decrypt a message that it has encrypted.
How to generate public & private keys in C
Let us generate public and private and implement it on a simple text to encrypt and decrypt the text.
Creating public key:
- Considering two prime numbers L = 53 and M = 59.
- Calculating Modulus (n) => n = L*M => n = 53*59 => n = 3127.
- In this context, we define modulus as the product of two large prime numbers.
- Defining e => e is basically a small exponent which must be an integer and relatively prime to λ(n) and 1 < e < λ(n). So, we consider e = 3.
- So our public key is (n, e), i.e. (3127, 3).
Creating private key:
1) Calculate λ(n): λ(n) is the totient function.
λ(n) = (L – 1)(M – 1)
λ(n) = (53 – 1)(59 – 1)
λ(n) = 3016.
The private key(d) = (k* λ(n) + 1) / e where k is some integer.
Let us define k = 2.
Hence d = 2011.
Implement public key (3127, 3) and private key (2011).
We will transfer the text “of” in a secured form using the above public key for encryption and the private key for decryption.
- Breakdown “hi” => h = 8 and i = 9.
- Encrypted data (en) => (89^e)mod n => (89^3)mod 3127 => 1394.
- Decrypted data (de) => (en^d)mod n => (1394^2011)mod 3127 => 89.
- Breakdown 89 => 8 = h and i = 9 => “hi” .
Working of RSA Algorithm in C
- The user will enter two prime numbers.
- Authenticate the two numbers.
- Assign the two numbers to the corresponding variables p and q.
- Calculate the product of p and q and store it in n.
- Determine the solution of the equation λ(n) = (p – 1)(q – 1).
- Select a random small exponent e ( e is basically a small exponent which must be an integer and relatively prime to λ(n) and 1 < e < λ(n) )
- Execute the equation d = e-1 mod n.
- Display the public key and private key.
- Seek a message from the user end.
- Convert the message into an encrypted format using the public key.
- Convert the encrypted format of text into a normal message using the corresponding private key.
- Print the message in both forms.
Code:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
long int flag, t, q, p, n,j, en[100], m[100], d[100], temp[100], e[100], i, a, b;
char msg[100];
void encrypt();
void decrypt();
void ce();
int prime(long int);
long int cd(long int);
int main() {
// Step 1- One by one, type the two prime numbers.
// Step 2- carry out Validation of numbers.
// Step 3 - Designate it to the variables.
// derive first prime number
do {
printf("Enter the first prime number : ");
if (scanf("%ld", &p) != 1 || !prime(p) || p == 1) {
printf("Invalid. Please enter a valid prime number only.\n");
while (getchar() != '\n')
; // Clear the input buffer
} else {
break;
}
} while (1);
// Get the second prime number
do {
printf("Enter the second prime number : ");
if (scanf("%ld", &q) != 1 || !prime(q) || q == 1 || p == q) {
printf("Invalid. Please enter a valid prime number only and different "
"from the first.\n");
while (getchar() != '\n')
; // Clear the input buffer
} else {
break;
}
} while (1);
// Step 9 Enter input message
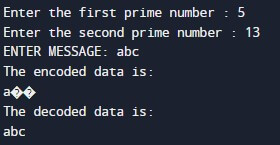
printf("ENTER MESSAGE: ");
scanf(" %[^\n]s", msg);
for (i = 0; i < strlen(msg); i++)
m[i] = msg[i];
// Step 4 Calculating the product of p and q
n = p * q;
// step 5 determine solution of totient equation
t = (p - 1) * (q - 1);
ce();
for (a = 0; a < j - 1; a++)
printf("%ld\t%ld\n", e[a], d[a]);
encrypt();
decrypt();
return 0;
}
int prime(long int prm) {
int b;
if (prm == 1)
return 0;
for (b = 2; b <= sqrt(prm); b++) {
if (prm % b == 0)
return 0;
}
return 1;
}
// step 8 public key
void ce() {
int k;
k = 0;
for (i = 2; i < t; i++) {
if (t % i == 0)
continue;
flag = prime(i);
if (flag == 1 && i != p && i != q) {
e[k] = i;
flag = cd(e[k]);
if (flag > 0) {
d[k] = flag;
k++;
}
if (k == 99)
break;
}
}
}
// step 8 private key
long int cd(long int x) {
long int k = 1;
while (1) {
k = k + t;
if (k % x == 0)
return (k / x);
}
}
// Step 10 Encryption process
void encrypt() {
long int pt, ct, key = e[0], k, len;
i = 0;
len = strlen(msg);
while (i < len) {
pt = m[i];
pt = pt - 96;
k = 1;
for (j = 0; j < key; j++) {
k = k * pt;
k = k % n;
}
temp[i] = k;
ct = k + 96;
en[i] = ct;
i++;
}
en[i] = -1;
printf("\nThe encoded data is:\n");
for (i = 0; en[i] != -1; i++)
printf("%c", (char)en[i]);
}
// Step 11 Decryption process
void decrypt() {
long int pt, ct, key = d[0], k;
a = 0;
while (en[a] != -1) {
ct = temp[a];
k = 1;
for (b = 0; b < key; b++) {
k = k * ct;
k = k % n;
}
pt = k + 96;
m[a] = pt;
a++;
}
m[a] = -1;
printf("\nThe decoded data is:\n");
for (a = 0; m[a] != -1; a++)
printf("%c", (char)m[a]);
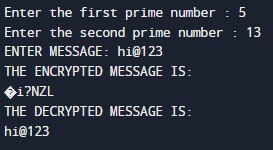
}Output:
Explanation:
- The user needs to type two prime numbers one by one.
- Then, n is calculated as a product of p and q.
- e, the small exponent is selected.
- The user is asked to enter a message. In our case, it is “abc”.
- Encryption performs the process, revealing the encryption outcome in the output.
- You decrypt to regain the original text.
Method and Approaches
1) Implementation of the RSA algorithm in C using a simple approach.
Code:
#include <stdio.h>
#include <math.h>
#include <string.h>
long long p, q, n, t, flag, e[100], d[100], temp[100], j, m[1000], en[1000], i;
char msg[1000];
int prime(long long);
void generateKeys();
long long modInverse(long long a, long long m);
void encrypt();
void decrypt();
long long getPrimeInput(const char *prompt);
int main() {
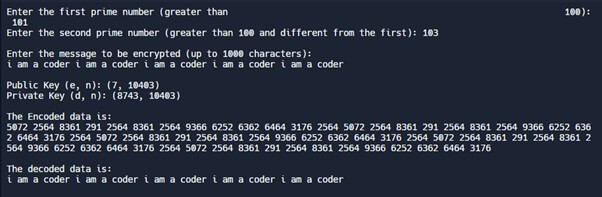
p = getPrimeInput("Enter the first prime number (greater than 100): ");
q = getPrimeInput("Enter the second prime number (greater than 100 and
different from the first): ");
printf("\nEnter the message to be encrypted (up to 1000 characters):\n");
scanf(" %[^\n]s", msg);
generateKeys();
printf("\nPublic Key (e, n): (%lld, %lld)\n", e[0], n);
printf("Private Key (d, n): (%lld, %lld)\n", d[0], n);
encrypt();
decrypt();
return 0;
}
int prime(long long pr) {
if (pr == 2 || pr == 3)
return 1;
if (pr == 1 || pr % 2 == 0)
return 0;
for (long long i = 3; i <= sqrt(pr); i += 2) {
if (pr % i == 0)
return 0;
}
return 1;
}
long long getPrimeInput(const char *prompt) {
long long num;
do {
printf("%s", prompt);
if (scanf("%lld", &num) != 1 || num <= 100 || !prime(num)) {
printf("Invalid input. Please enter a valid prime number.\n");
while (getchar() != '\n') {} // Clear the input buffer
} else {
break;
}
} while (1);
return num;
}
void generateKeys() {
n = p * q;
t = (p - 1) * (q - 1);
for (long long i = 2; i < t; i++) {
if (t % i == 0)
continue;
flag = prime(i);
if (flag == 1 && i != p && i != q) {
e[0] = i;
break;
}
}
d[0] = modInverse(e[0], t);
}
long long modInverse(long long a, long long m) {
long long m0 = m, t, q;
long long x0 = 0, x1 = 1;
if (m == 1)
return 0;
while (a > 1) {
q = a / m;
t = m;
m = a % m;
a = t;
t = x0;
x0 = x1 - q * x0;
x1 = t;
}
if (x1 < 0)
x1 += m0;
return x1;
}
void encrypt() {
printf("\nThe Encoded data is:\n");
for (i = 0; i < strlen(msg); i++) {
m[i] = msg[i];
long long pt = m[i];
long long ct = 1;
for (j = 0; j < e[0]; j++) {
ct = (ct * pt) % n;
}
en[i] = ct;
printf("%lld ", ct);
}
en[i] = -1;
printf("\n");
}
void decrypt() {
printf("\nThe decoded data is:\n");
for (i = 0; en[i] != -1; i++) {
long long ct = en[i];
long long pt = 1;
for (j = 0; j < d[0]; j++) {
pt = (pt * ct) % n;
}
m[i] = pt;
printf("%c", (char)m[i]);
}
printf("\n");
}Output:
Explanation:
- The system initially prompts the user to enter prime numbers greater than 100, then calculates n. While entering the prime numbers, logic checks whether the input is numeric, prime number, or greater than 100. This selection of large prime numbers increases the security.
- Calculating and displaying public and private keys.
- Encryption: The user is asked to enter the message. The public key converts the message into an encrypted format.
- Decryption: The private converts the encrypted format of the message into its original form.
- The Printf function prints the required messages as shown in the output.
2) Additional RSA Algorithm Programming
Code:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
long isPomod(long c, long d, long m)
{
long x = 1, y = c;
while (d > 0)
{
if (d % 2 == 1)
{
x = (x * y) % m;
}
y = (y * y) % m;
d /= 2;
}
return x % m;
}
int isRandome(int lambda_nm)
{
printf("\nThe number e should be greater than 1 and less than %d",
lambda_nm);
for (int a = 2; a < lambda_nm; a++)
{
if (isGcd(a, lambda_nm) == 1)
{
return a;
}
}
return -1;
}
int isPrimeNumber(long nm)
{
if (nm < 2)
return 0;
for (long a = 2; a <= sqrt(nm); a++)
{
if (nm % a == 0)
{
return 0;
}
}
return 1;
}
int key_private(int e, int lambda_nm)
{
for (int c = 1; c < lambda_nm; c++)
{
if ((c * e) % lambda_nm == 1)
{
printf("\nHence, (c * e) %% lambda_nm = 1, (%d * %d) %% %d = 1",
c, e, lambda_nm);
return c;
}
}
return -1;
}
char *encrypt_msg(char *inputmessage, long e, long n)
{
long i;
long lenn = strlen(inputmessage);
char *cipher_algo = (char *)malloc(lenn * sizeof(char));
for (i = 0; i < lenn; i++)
{
cipher_algo[i] = isPomod(inputmessage[i], e, n);
printf("\n%c -> %ld", inputmessage[i], cipher_algo[i]);
}
return cipher_algo;
}
char *decrypt_msg(char *cipher_algo, long d, long n)
{
long i;
long lenn = strlen(cipher_algo);
char *decodedmessage = (char *)malloc(lenn * sizeof(char));
for (i = 0; i < lenn; i++)
{
decodedmessage[i] = isPomod(cipher_algo[i], d, n);
printf("\n%ld -> %c", cipher_algo[i], decodedmessage[i]);
}
return decodedmessage;
}
int isTotient(int p, int q)
{
return (p - 1) * (q - 1);
}
int isGcd(int c, int d)
{
if (c == 0)
{
return d;
}
return isGcd(d % c, c);
}
int main()
{
int p, q, lambda_nm;
long n, e, d;
char *inputmessage;
char *cipher_algo;
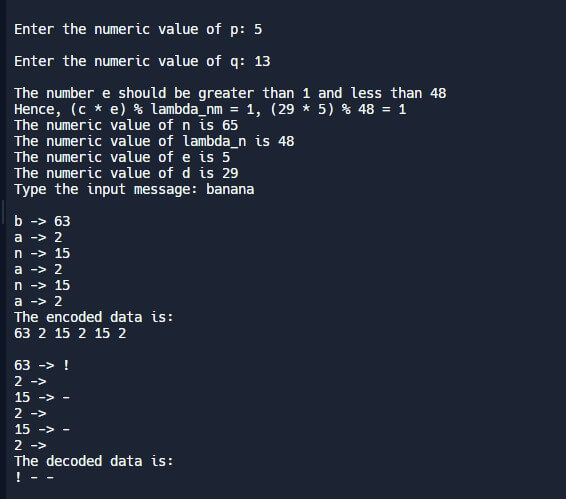
printf("\nEnter the numeric value of p: ");
scanf("%d", &p);
printf("\nEnter the numeric value of q: ");
scanf("%d", &q);
if (isPrimeNumber(p) && isPrimeNumber(q))
{
n = p * q;
lambda_nm = isTotient(p, q);
e = isRandome(lambda_nm);
d = key_private(e, lambda_nm);
printf("\nThe numeric value of n is %ld", n);
printf("\nThe numeric value of lambda_n is %d", lambda_nm);
printf("\nThe numeric value of e is %ld", e);
printf("\nThe numeric value of d is %ld", d);
inputmessage = (char *)malloc(sizeof(char) * 100);
printf("\nType the input message: ");
scanf(" %[^\n]", inputmessage);
cipher_algo = encrypt_msg(inputmessage, e, n);
puts("\nThe encoded data is: ");
for (int i = 0; cipher_algo[i] != '\0'; i++)
{
printf("%ld ", cipher_algo[i]);
}
printf("\n");
inputmessage = decrypt_msg(cipher_algo, d, n);
puts("\nThe decoded data is: ");
printf("%s\n", inputmessage);
free(inputmessage);
}
else
{
printf("\nThe numeric value of p and q should be a prime number.");
}
return 0;
}Output:
This approach mainly concentrates on storing data in a temporary array. During decoding, we will make use of it.
Explanation:
- The isPrime function checks whether the entered numbers are prime.
- The gcd() function determines the greatest common divisor of both inputs.
- The Totient function calculates the value of n.
- The random function determines the exponent “e” randomly.
- The function private_key calculates the Private key.
- The square and multiply method employs the “pomod” function.
- The encryption process converts the message into encrypted form by converting each character.
- Perform the decryption process for each cipher character.
- The system dynamically provides memory to the input message and ciphertext.
- Freeing memory prevents memory leaks after performing the encryption and decryption process.
- We have also used “malloc”, which is memory allocation. This serves as memory during code execution.
Examples a program in C
In this example, we will input a message containing text, numbers, and symbols.
Code:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
char input_msg[100];
long int t, p, q, n, d[100], temp[100], e[100], m[100], j, isFlag, i, en[100];
long int cd(long int);
void ce();
int isPrime(long int);
void encrypt_msg();
void decrypt_msg();
long int cd(long int z) {
long int y = 1;
while (1) {
y = y + t;
if (y % z == 0)
return (y / z);
}
}
void ce() {
int y;
y = 0;
for (i = 2; i < t; i++) {
if (t % i == 0)
continue;
isFlag = isPrime(i);
if (isFlag == 1 && i != p && i != q) {
e[y] = i;
isFlag = cd(e[y]);
if (isFlag > 0) {
d[y] = isFlag;
y++;
}
if (y == 99)
break;
}
}
}
int isPrime(long int prm) {
int a;
if (prm == 1)
return 0;
for (a = 2; a <= sqrt(prm); a++) {
if (prm % a == 0)
return 0;
}
return 1;
}
void encrypt_msg() {
long int py, cy, key = e[0], z, lenn;
i = 0;
lenn = strlen(input_msg);
while (i < lenn) {
py = m[i];
py = py - 96;
z = 1;
for (j = 0; j < key; j++) {
z = z * py;
z = z % n;
}
temp[i] = z;
cy = z + 96;
en[i] = cy;
i++;
}
en[i] = -1;
printf("\nThe encoded data is:\n");
for (i = 0; en[i] != -1; i++)
printf("%c", (char)en[i]);
}
void decrypt_msg() {
long int py, cy, key = d[0], z;
i = 0;
while (en[i] != -1) {
cy = temp[i];
z = 1;
for (j = 0; j < key; j++) {
z = z * cy;
z = z % n;
}
py = z + 96;
m[i] = py;
i++;
}
m[i] = -1;
printf("\nThe decoded data is:\n");
for (i = 0; m[i] != -1; i++)
printf("%c", (char)m[i]);
}
int main() {
do {
printf("Type the first prime number : ");
if (scanf("%ld", &p) != 1 || !isPrime(p) || p == 1) {
printf("Invalid input. Please type a legitimate prime number only.\n");
while (getchar() != '\n')
;
} else {
break;
}
} while (1);
do {
printf("Enter the second prime number : ");
if (scanf("%ld", &q) != 1 || !isPrime(q) || q == 1 || p == q) {
printf("Invalid input. Please enter a legitimate prime number only and
different "
"from the first prime number.\n");
while (getchar() != '\n')
;
} else {
break;
}
} while (1);
printf("Enter input message: ");
scanf(" %[^\n]s", input_msg);
for (i = 0; i < strlen(input_msg); i++)
m[i] = input_msg[i];
n = p * q;
t = (p - 1) * (q - 1);
ce();
for (i = 0; i < j - 1; i++)
printf("%ld\t%ld\n", e[i], d[i]);
encrypt_msg();
decrypt_msg();
return 0;
}
Output:
Explanation:
- The user is requested to enter two prime numbers.
- The program executes and determines the value of n as a product of p and q.
- It also calculates the totient function. The public and corresponding private key is derived.
- The user enters the desired input message. In our case, the input message consists of letters, numbers, and symbols.
- The public key converts the input message into an encrypted format.
- Later, the decryption process uses the private key to restore the input message to its original form.
- Display all the results in the output.
Advantages
- Authentic communication: The public key encrypts messages, while the private key decrypts messages and authenticates users.
- Additional security: The algorithm for secure data transmission does not require sharing any key through the internet.
- Data Integrity: Data remains unchanged during the transmission process.
- Efficient transmission: The RSA algorithm is used widely as RSA encryption and is faster than other methods.
- Due to its complex mathematical factors, It is challenging to break into its transmission system and cause harm to the data.
- It has become a standard choice for the user when it comes to data transmission.
Disadvantages
- Large key consideration: A secure algorithm uses a large key, which demands more processing time, power, and storage space.
- Low performance: The processing rate is poor for encrypting and decrypting vast amounts of information.
- RSA and attackers: Attackers might extract sensitive information by analyzing the time required, electromagnetic radiation, and power used during the cryptographic operation.
- Its limited application stems from its slower RSA decryption speed compared to other algorithms.
Conclusion
The RSA algorithm widely secures data during transmission by factoring two large prime numbers and uses modular exponentiation for a fast encryption process. It has great applications for securing electronic signatures, virtual private networks, email messaging, and person-to-person communication. The RSA algorithm is versatile because various libraries support it, and it finds applications in C programming. It maintains data security, integrity, and authenticity.
FAQ
Q1. How do you avoid integer overflow during RSA implementation?
Answer: To avoid integer overflow use modular arithmetic techniques for a defined range of numbers, use *long long int* datatype for a larger range, or use GNU Multiple Precision Arithmetic library for more large integers.
Q2. How to implement side-channel attack-resistant RSA?
Answer: For resisting attacks, perform a constant-time algorithm that executes fixed instructions for all inputs, implement masking techniques to shield processed data from any observer, and install software guard protection for better protection.
Q3. What are the most common tools to resolve RSA implementation issues?
Answer: Use debugging tools like Valgrind and GDB to resolve runtime and undefined errors, perform unit testing, and use references from open-source libraries and code.
Q4. Can multiple public keys be generated for a single private key?
Answer: No. According to the RSA algorithm, a private key will have only one corresponding public key.
Recommended Articles
We hope this EDUCBA information on “RSA algorithm in C” benefited you. You can view EDUCBA’s
recommended articles for more information.