Updated March 28, 2023

Introduction to Selection Sort in C++
Selection sort is a sort algorithm which uses to sort the array of n elements. In Selection sort, every pass finds the smallest element and inserts it to the correct position in an array. An algorithm works on two sub array. First subarray which store sorted elements and second subarray which store unsorted elements. In every pass of selection, sort finds the smallest element from the unsorted array and placed to the sorted array. In simple the first pass finds the smallest element and places it in the first position. And in the second pass it finds the second smallest element and places it on the second position and so on. The process is repeated till all the elements of an array is sorted.
Selection Sort Logic
Let’s take an array L which is having n number of elements and which are to be sort by using selection sort. So the selection sort algorithm processes in the following pass.
- I Pass: Find the smallest element in an array with its index. And then swap L[0] with L[index]. The result of this pass is, we have L[0] sorted subarray and n-1 elements are to be sort unsorted subarray.
- II Pass: Find the smallest element in unsorted subarray with its index. And then swap L[1] with L[index]. The result of this pass is, we have L[0] and L[1] sorted subarray and n-1 elements are to be sort unsorted subarray, and so on.
- Similarly, it performs n-1 passes and in n-1 pass, finds the smallest element in unsorted subarray with its index. And then swap L[n-1] with L[index]. The result of this pass is, we have L[0] to L[n-1] are sorted as sorted subarray and no more elements are to be sort.
Let’s see how above passes works with an example, so let’s take an array of 5 elements an example L = [ 6, 2, 5, 3, 9 ], which are to be sort using selection sort as:
- I Pass: [ 6, 2, 5, 3, 9 ] –> [ 2, 6, 5, 3, 9 ], Algorithm start by finding the first smallest number in L[0] to L[4] and place it at L[0].
- II Pass: [ 2, 6, 5, 3, 9 ] –> [ 2, 3, 5, 6, 9 ], find the smallest number in range L[1] to L[4] and place it at L[1].
- III Pass: [ 2, 3, 5, 6, 9 ] –> [ 2, 3, 5, 6, 9 ], find the smallest number in range L[2] to L[4] and place it at L[2].
- IV Pass: [ 2, 3, 5, 6, 9 ] –> [ 2, 3, 5, 6, 9 ], find smallest number in range L[3] to L[4] and place it at L[3].
Now, an array is sorted after all n-1 pass.
Selection Sort Algorithm
Consider L is an array which is having n number of elements. So selection sort algorithm to sort the given L array algorithm is:
Algorithm:
begin Selection_Sort (L, N)
for i = 1 to N-1
call small (L, i, N, index)
swap L[i] with L[index]
end for
return L
end Selection_Sort
begin small (L, i, N, index)
initialize small = L[i]
initialize index = i
for J = i+1 to N -1
if small > L[j]
small = L[j]
index = j
end if
end for
return index
end smallThe Complexity of Selection Sort Technique:
- Best Case Running Time: Ω( n )
- Average Case Running time Complexity: θ( n2 )
- Worst Case Running time Complexity: o( n2 )
- Space Complexity: o( 1 )
Examples to Implement Selection Sort in C++
Next, we write the c++ code to understand the selection sort technique more clearly with the following example where we use the selection sort technique inside for loop to apply on array elements.
Example #1
Code:
#include<iostream>
using namespace std;
int small(int L[], int n, int i);
int main ()
{
int i, j, k, index, t;
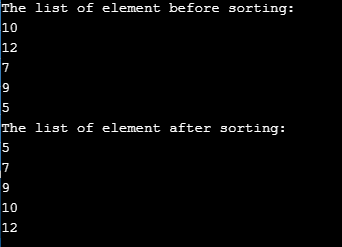
int L[10] = { 10, 12, 7, 9, 5 };
cout << "The list of element before sorting:" <<endl;
for(i = 0; i < 5; i++)
{
cout<<L[i]<<endl;
}
for( i = 0;i < 5; i++)
{
index = small(L, 5, i);
t = L[i];
L[i] = L[index];
L[index] = t;
}
cout << "The list of element after sorting:" <<endl;
for(i = 0; i < 5; i++)
{
cout<<L[i]<<endl;
}
return 0;
}
int small(int L[], int n, int i)
{
int s, index, j;
s = L[i];
index = i;
for( j = i+1; j < 5; j++)
{
if(L[j] < s )
{
s = L[j];
index = j;
}
}
return index;
}Output:
Next, we write the c++ code and we write the bubble sort technique inside a function, which we will be call and pass an array.
Example #2
Code:
#include<iostream>
using namespace std;
void disp( int *L )
{
int i;
for(i = 0; i < 5; i++)
{
cout<<L[i]<<endl;
}
}
int small(int L[], int n, int i);
void Selection_Sort(int *L, int N )
{
int t, i, index;
for( i = 0;i < N; i++)
{
index = small(L, N, i);
t = L[i];
L[i] = L[index];
L[index] = t;
}
}
int main ()
{
int i, j, N=5;
int L[10] = { 10, 12, 7, 9, 5 };
cout << "The list of element before sorting:" <<endl;
disp(L);
Selection_Sort( L, N );
cout << "The list of element after sorting:" <<endl;
disp(L);
return 0;
}
int small(int L[], int n, int i)
{
int s, index, j;
s = L[i];
index = i;
for( j = i+1; j < 5; j++)
{
if(L[j] < s )
{
s = L[j];
index = j;
}
}
return index;
}Output:
Conclusion
In Selection sort algorithm every pass finds the smallest element and insert it to the correct position in an array. An array with n elements need (n-1) passes to sort them. The complexity of selection sort algorithm is O( n2 ).
Recommended Article
This is a guide to Selection Sort in C++. Here we discuss the Introduction to Selection Sort in C++ and its Examples along with Code Implementation and Output. you can also go through our suggested articles to learn more –