Updated March 6, 2023
Definition of Skip List
Skip list in Computer Science is considered as a probabilistic data structure where it is allowed for the array, linked list, and other data structures to compute values each associated with some kind of search complexities. Skip list gels well with the set of sorted arrays were searching and manipulation of elements within it gets enhanced and efficient. It also allows linked list data structure to maintain insertion order and other elements operation at a faster pace especially in terms of accessibility. Searching with skip list gets initiated with each subsequence of elements by skipping the irrelevant one.
How does Skip list works?
The entire skip list has significance in how it works is let’s see this with a real-time example.
Suppose a superfast train is running but it does not encounter all the stops at one go so in that case, it is the selected stations where the train will be stopped hence it is mostly preferred by the people because of its ease of accessibility and less time consumption.
Let’s discuss the algorithm with an example and also calculate its time complexity.
According to the algorithm which Skip list follows there are four main important steps which are followed:
Search: This is the main and the initial operation where the input given to the function is in the form of a key and then the output to be estimated is a position p where the value for this position is considered largest or less than or equal to the estimated value. Scanning takes place in the top to bottom approach then the scanning is forwarded.
Algo:
Search_Key (Key_0)
p_0 = top_left node for_search
while (p_0 down ! = null) do
p_0 = p_0.down
while (key_0 >= p_0.next) do
p_0 = p_0.next
return p_0
Indexing: Indexing operation with its behavior is almost same as search process therefore we will not write any pseudocode for this it will be exactly similar to the Search_Key() function algorithm.
Insertion: Insertion operation is the next operation preferred after indexing where again the input fed to the function is a key then the expected output is the topmost position of the for which the input is being fed for within the hierarchy. So here a coin flip approach of head and tail with a deterministic approach is selected where if element inserted is a then the other element to be inserted will be b only.
Insert (Key_0)
P_1 = Search_Key(Key_0)
q_0 = null
k_1 = 1
repeat
K_1 = k_1 + 1
If k_1 > = height_0
Height = height_0+1
createNewLevelLinked_List()
while (P_1.up == null)
P_1 = P_1.previous_0
P_1 = P_1.above_0
q_0 = insertAfterKey(Key_0, P_1)
until coinFlip == ‘Tails_val’
j_0 = j_0 +1
return q_0
Deletion: Deletion is the last operation which skips list follows and plays around with the elements. Deletion operation gets aid and takes help from the search operation and it is quite easier in usage when compared to actual insertion operation. Also, delete function makes its use in a way where once connected helps in deleting all the associated components or node to it. Only one deletion is needed to be triggered at one go.
Delete (key_0)
Start searching keys which are needed to be manipulated for all the positions from p_0 to…p_n where almost all keys exist
If nothing is found
Return val_0
Then, delete all the attached_nodes_from position p_0….p_n
Remove all vacant layers attached in the hierarchy tree and reduce the complexity.
Example
This program demonstrates the skip list in C++ where the creation of node, followed by insertion and display of element takes place as shown in the output.
#include <bits/stdc++.h>
using namespace std;
class Node_0
{
public:
int key_1;
Node_0 **forward_ptr;
Node_0(int, int);
};
Node_0::Node_0(int key_1, int levl_0)
{
this->key_1 = key_1;
forward_ptr = new Node_0*[levl_0+1];
memset(forward_ptr, 0, sizeof(Node_0*)*(levl_0+1));
};
class SkipList_2
{
int MAXLVL_5;
float P_0;
int level_2;
Node_0 *header_1;
public:
SkipList_2(int, float);
int randomLevel_8();
Node_0* createNode_0(int, int);
void insertElement_1(int);
void displayList_3();
};
SkipList_2::SkipList_2(int MAXLVL_5, float P_0)
{
this->MAXLVL_5 = MAXLVL_5;
this->P_0 = P_0;
level_2 = 0;
header_1 = new Node_0(-1, MAXLVL_5);
};
int SkipList_2::randomLevel_8()
{
float r_5 = (float)rand()/RAND_MAX;
int lvl_1 = 0;
while (r_5 < P_0 && lvl_1 < MAXLVL_5)
{
lvl_1++;
r_5 = (float)rand()/RAND_MAX;
}
return lvl_1;
};
Node_0* SkipList_2::createNode_0(int key, int level_3)
{
Node_0 *n_9 = new Node_0(key, level_3);
return n_9;
};
void SkipList_2::insertElement_1(int key)
{
Node_0 *current = header_1;
Node_0 *update[MAXLVL_5+1];
memset(update, 0, sizeof(Node_0*)*(MAXLVL_5+1));
for (int i = level_2; i >= 0; i--)
{
while (current->forward_ptr[i] != NULL &&
current->forward_ptr[i]->key_1 < key)
current = current->forward_ptr[i];
update[i] = current;
}
current = current->forward_ptr[0];
if (current == NULL || current->key_1 != key)
{
int rlevel = randomLevel_8();
if (rlevel > level_2)
{
for (int i=level_2+1;i<rlevel+1;i++)
update[i] = header_1;
level_2 = rlevel;
}
Node_0* n_1 = createNode_0(key, rlevel);
for (int i=0;i<=rlevel;i++)
{
n_1->forward_ptr[i] = update[i]->forward_ptr[i];
update[i]->forward_ptr[i] = n_1;
}
cout << "Successfully_Key_Inserted.. " << key << "\n";
}
};
void SkipList_2::displayList_3()
{
cout<<"\n**Skip_List_To_Display"<<"\n";
for (int i=0;i<=level_2;i++)
{
Node_0 *node = header_1->forward_ptr[i];
cout << "Levels_to_define " << i << "::: ";
while (node != NULL)
{
cout << node->key_1<<" ";
node = node->forward_ptr[i];
}
cout << "\n";
}
};
int main()
{
srand((unsigned)time(0));
SkipList_2 lst_0(4, 2.3);
lst_0.insertElement_1(2);
lst_0.insertElement_1(6);
lst_0.insertElement_1(13);
lst_0.insertElement_1(40);
lst_0.insertElement_1(12);
lst_0.insertElement_1(19);
lst_0.insertElement_1(18);
lst_0.insertElement_1(20);
lst_0.insertElement_1(11);
lst_0.insertElement_1(12);
lst_0.displayList_3();
}
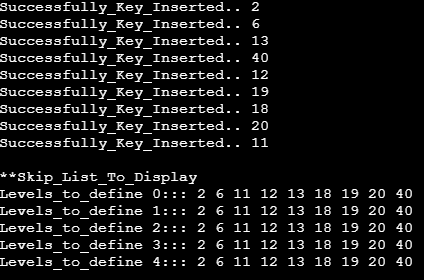
Output:
Explanation:
In the above program first, a class is implemented in order to create a node then an array is declared to hold pointers of different nodes of the level where then a specific set of memory gets allocated which then gets filled with a forwarded set of values to perform various operations like search, filter, traverse and many more which then helps in the insertion of elements within the list for display as shown in the output as well.
Conclusion
Skip List is used as a beneficial process in terms of computation and makes it useful when it comes to implementation from the developer’s perspective. It also makes everyone aligned and helps in making statistical concurrent priority with less lock contention for proper and efficient utilization with queues for the proper manipulation and operation.
Recommended Articles
This is a guide to Skip List. Here we discuss the Definition, syntax, How Skip list works? with Examples with code implementation. You may also have a look at the following articles to learn more –