Updated July 5, 2023

Introduction to Spanning Tree in Data Structure
The following article provides an outline for Spanning Tree in Data Structure. In the data structure, we have different types of trees. The spanning tree is one of the types of trees. A spanning tree is a subset of graph G; it covers all vertices with a minimum value of edges in the spanning tree. Furthermore, the spanning tree does not contain any cycle, which means we can say that the spanning tree is a graph, and it uses some terminology of the graph.
The spanning tree includes all edges in the graph, meaning the number of edges should be the same. Disconnected does not allow in spanning tree means we cannot remove any single edge from the spanning tree, and when we add edge into the spanning tree that creates the cycle and cyclic tree does not allow in spanning tree.
Algorithm
We used two types of algorithms to find the minimum spanning tree.
1. Prim’s Algorithm
Function prims(ver, edg)
Edg_t = {edge with minimum weight in edg}
Repeat n-2 times
E = find the adjacent edge in Edg_t, and it does not contain the cycle, and it has minimum weight.
Edg_t = Edg_t + {E}
Return (ver, Edg_t)
Explanation:
- In Prim’s algorithm, we always start with the minimum edge from the spanning tree. After that, we need to find the adjacent minimum edge from the current edge of the spanning tree and repeat this process until the n-1 of edges.
2. Kruskal’s Algorithm
Function kruskal(ver, edg)
Edg_t = { }
Repeat n-1 times
E = find the adjacent minimum weight edge from the spanning tree.
Edg_t = Edg_t + {E}
Return (ver, Edg_t)
Explanation:
- The working of the Kruskal algorithm is the same as Prim’s algorithm. The only difference is that we don’t have a search limit.
How Spanning Tree Works in Data Structure?
Now let’s see how spanning trees work in a data structure as follows:
Suppose we have a graph containing the vertices and edges of G (V, E).
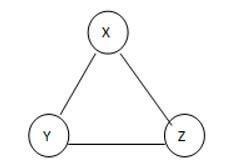
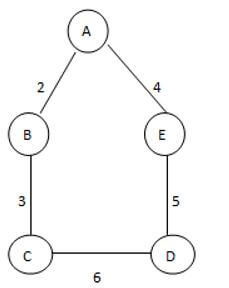
Consider the following example as follows.
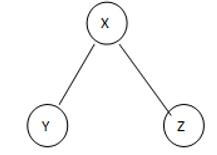
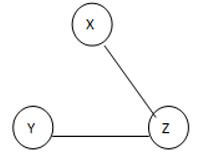
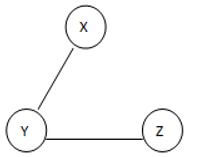
This is a given graph that is G, and we need to find the Spanning of this graph, see here we can generate the three different spanning trees as follows.
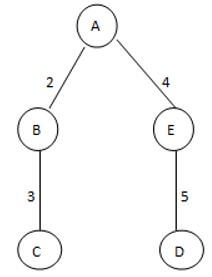
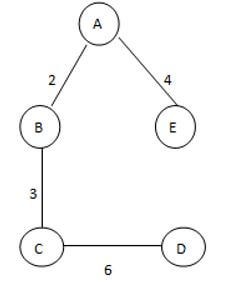
ST 1
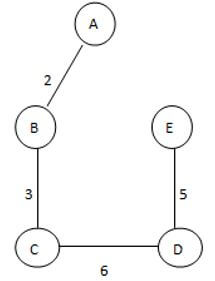
ST 2
ST 3
See here we found three different spannings from graph G; we know that the complete undirected graph has a maximum Vv-2 number of spanning trees, where V is the number of vertices from the graph, so in this graph V = 3 so 3 spanning trees are possible.
Properties of Spanning Tree:
- The graph contains more than one spanning tree.
- All spanning trees of the graph contain the same number of edges and vertices.
- The spanning tree does not contain the loops that mean cycle.
- When we remove edges from the spanning tree that is spanning tree, we call it a minimal connected.
- When we remove edges from the spanning tree that is spanning tree, we call it maximal connected.
Now consider the following graph for the Spanning tree as follows.
The possible different spanning trees of the above graph are as below.
SP 1_14
SP 2_16
SP 3_15
In the above figure, we draw the possible spanning tree from the graph, here, we also specify the weight of the edge, and the first tree we call the minimum spanning tree with a weight is 14, as shown in SP 1_14.
Examples of Spanning Tree in Data Structure
Given below are the different examples of spanning trees.
Normally, we can use two different algorithms to implement the spanning tree: Prim’s and Kruskal’s algorithms.
Example #1
Prim’s Program using Python is as follows.
Code:
INF = 999999
Ver = 5
Graph = [[0, 10, 65, 0, 0],
[4, 0, 5, 20, 47],
[55, 85, 0, 55, 63],
[0, 21, 41, 0, 71],
[0, 22, 36, 25, 0]]
Choose = [0, 0, 0, 0, 0]
num_edge = 0
Choose[0] = True
print("Edge of graph : with Weight\n")
while (num_edge < Ver - 1):
min = INF
A = 0
B = 0
for i in range(Ver):
if Choose[i]:
for j in range(Ver):
if ((not Choose[j]) and Graph[i][j]):
if min > Graph[i][j]:
min = Graph[i][j]
A = i
B = j
print(str(A) + "-" + str(B) + ":" + str(Graph[A][B]))
Choose[B] = True
num_edge += 1Explanation:
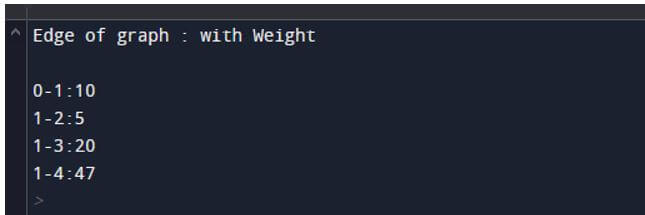
- Using Prim’s program above, we try to implement a minimum spanning tree. Here we first define the number of vertices. Then, we also specify the graph’s adjacency matrix as shown in the above program.
- We illustrate the final output of the above statement using the following snapshot.
Output:
Example #2
Now let’s see an example of the Kruskal algorithm as follows.
Code:
class K_Graph:
def __init__(self, ver):
self.V = ver
self.graph = []
def add_edg(self, u, v, w):
self.graph.append([u, v, w])
# Search function
def find(self, par, i):
if par[i] == i:
return i
return self.find(par, par[i])
def apply_union(self, par, R, A, B):
Aroot = self.find(par, A)
Broot = self.find(par, B)
if R[Aroot] < R[Broot]:
par[Aroot] = Broot
elif R[Aroot] > R[Broot]:
par[Aroot] = Aroot
else:
par[Broot] = Aroot
R[Aroot] += 1
# Applying Kruskal algorithm
def kru_algo(self):
res = []
i, e = 0, 0
self.graph = sorted(self.graph, key=lambda value: value[2])
par = []
R = []
for ver in range(self.V):
par.append(ver)
R.append(0)
while e < self.V - 1:
u, v, w = self.graph[i]
i = i + 1
A = self.find(par, u)
B = self.find(par, v)
if A != B:
e = e + 1
res.append([u, v, w])
self.apply_union(par, R, A, B)
for u, v, weight in res:
print("%d - %d: %d" % (u, v, weight))
gr = K_Graph(6)
gr.add_edg(0, 1, 5)
gr.add_edg(0, 2, 2)
gr.add_edg(1, 2, 6)
gr.add_edg(1, 0, 8)
gr.add_edg(2, 0, 3)
gr.add_edg(2, 1, 1)
gr.add_edg(2, 3, 4)
gr.add_edg(2, 5, 3)
gr.add_edg(2, 4, 5)
gr.add_edg(3, 2, 4)
gr.add_edg(3, 4, 4)
gr.add_edg(4, 2, 5)
gr.add_edg(4, 3, 2)
gr.add_edg(5, 2, 1)
gr.add_edg(5, 4, 4)
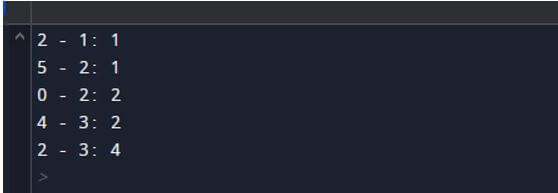
gr.kru_algo()Explanation:
- We illustrate the final output of the above statement using the following snapshot.
Output:
Conclusion
From the above article, we have seen the basic syntax of the spanning tree and different examples of the Spanning tree. We have seen how and when we use the Spanning tree in the data structure from this article.
Recommended Articles
We hope that this EDUCBA information on “Spanning Tree in Data Structure” was beneficial to you. You can view EDUCBA’s recommended articles for more information.