Updated March 6, 2023

Introduction to Splay Tree in Data Structure
Splay tree in data structure is actually a variant or type of binary search tree which is capable of self-adjusting and self-balancing functionality. In this type of data structure whenever any operation is carried out on the tree it is followed by a special operation called as splay. The slay operation involves rearrangement of the data nodes in the tree so that the current element which the operations are being carried out is set to as the root node of the tree data structure. In this article, we will study about splay tree, the operations which are carried out on the splay tree and the how splay tree can be implemented by using C programming language.
Splay Trees
Before we begin with the splay trees, it is required that you have a little knowledge about binary tree in which all the values less than the root node are present on the left side of the root while all the nodes whose values are greater than those of root node are placed on the right side of the root. The time complexity of binary search tree, when considered averagely for each node, is O(logn) while in worst case scenario the time complexity of binary tree is O(n). When the binary tree is either right-skewed or left-skewed then the time complexity is always O(n). Hence, to avoid this AVL and red-black trees were used so that the complexity for all the cases will be O(logn).
Some of the additional features were introduced in a splay tree which make it even more efficient than AVL and red-black trees when implemented in practical. Along with all the common operations like insert, delete and search, Splay tree also does the splay operation which rearranges the tree and brings the node to be operated in the root place. Whenever any of the above-mentioned operation is carried out then prior to that the algorithm also performs the splay operation. Hence, we can say that the splay trees are roughly balanced trees.
Operations in Splay Tree
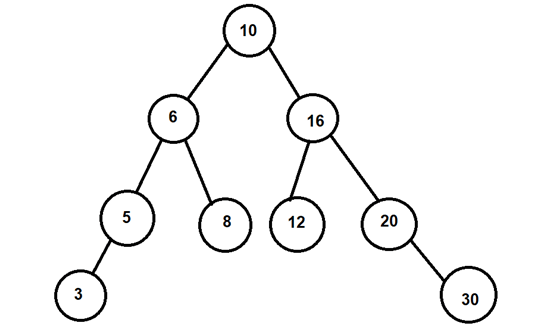
Consider that we have seven elements in the tree as shown below:
Now, in case if we want to perform the search operation then we will perform the simple binary search firstly which means that as 6 is less than 10 then we will go on the right side. After doing this search operation, the algorithm will perform splaying which will rearrange all the nodes and the node which is operated will be brought to root by performing rotations.
Rotations
There are a total of six types of rotations that are carried out –
- Zig: When the left rotation is performed.
- Zag: When right rotation is carried out.
- Zig zag: When we perform zig followed by zag that means right followed by left.
- Zag zig: When we perform zag followed by zig that means left followed by the right.
- Zig zig: When two right operations are carried out.
- Zag zag: When two left operations are performed.
Selection of type of rotation to be performed
The algorithm executes the above-mentioned rotations depending on certain factors which are as follows –
- The node on which operations are performed has grandparent or not.
- The operating node is on the right or left side of the immediate parent.
- The operating node is on the right or left side of the grand parent.
Possible cases for determining type of rotation
- Case 1: If the node is on the right side of the immediate parent and not having the grand parent then left rotation is performed or else if the node does not have the grand parent and is on the left side of an immediate parent the right rotation is performed.
- Case 2: The following scenarios are considered when the node does not have the grandparent –
- Scenario 1: If the operating node, as well as the immediate parent, are on the right side then zig zig operation which is right right rotation is carried out.
- Scenario 2: If the operating node is at left of the parent and the parent itself is at the right side of its own immediate parent then zig-zag which means the right-left operation is performed.
- Scenario 3: If both the operating node and the parent are on the right side of their immediate parents then zag zag which means left left operation is performed.
- Scenario 4: If the operating node is on right side and the parent is on the left side then zag zig operation which is a left-right operation is carried out.
Example of Splay Tree in Data Structure
In the below example, l_node is the left node, r_node is the right side node, n_node is for the new node and p_node is the parent node. The sPlayTree_DS is for the splay tree data structure struct that is created.
Code:
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int data;
struct node * l_node;
struct node * r_node;
struct node * p_node;
}node;
typedef struct sPlayTree_DS {
struct node * root_node;
}sPlayTree_DS;
node* n_node(int data) {
node *n = malloc(sizeof(node));
n->data = data;
n-> p_node = NULL;
n-> r_node = NULL;
n-> l_node = NULL;
return n;
}
sPlayTree_DS* new_sPlayTree_DS() {
sPlayTree_DS *t = malloc(sizeof(sPlayTree_DS));
t-> root_node = NULL;
return t;
}
node* maximum(sPlayTree_DS *t, node *x) {
while(x-> r_node != NULL)
x = x-> r_node;
return x;
}
void l_node_rotate(sPlayTree_DS *t, node *x) {
node *y = x-> r_node;
x-> r_node = y-> l_node;
if(y-> l_node != NULL) {
y-> l_node-> p_node = x;
}
y-> p_node = x-> p_node;
if(x-> p_node == NULL) { //x is root_node
t-> root_node = y;
}
else if(x == x-> p_node-> l_node) { //x is l_node child
x-> p_node-> l_node = y;
}
else { //x is r_node child
x-> p_node-> r_node = y;
}
y-> l_node = x;
x-> p_node = y;
}
void r_node_rotate(sPlayTree_DS *t, node *x) {
node *y = x-> l_node;
x-> l_node = y-> r_node;
if(y-> r_node != NULL) {
y-> r_node-> p_node = x;
}
y-> p_node = x-> p_node;
if(x-> p_node == NULL) { //x is root_node
t-> root_node = y;
}
else if(x == x-> p_node-> r_node) { //x is l_node child
x-> p_node-> r_node = y;
}
else { //x is r_node child
x-> p_node-> l_node = y;
}
y-> r_node = x;
x-> p_node = y;
}
void splay(sPlayTree_DS *t, node *n) {
while(n-> p_node != NULL) { //node is not root_node
if(n-> p_node == t-> root_node) { //node is child of root_node, one rotation
if(n == n-> p_node-> l_node) {
r_node_rotate(t, n-> p_node);
}
else {
l_node_rotate(t, n-> p_node);
}
}
else {
node *p = n-> p_node;
node *g = p-> p_node; //grand p_node
if(n-> p_node-> l_node == n && p-> p_node-> l_node == p) { //both are l_node children
r_node_rotate(t, g);
r_node_rotate(t, p);
}
else if(n-> p_node-> r_node == n && p-> p_node-> r_node == p) { //both are r_node children
l_node_rotate(t, g);
l_node_rotate(t, p);
}
else if(n-> p_node-> r_node == n && p-> p_node-> l_node == p) {
l_node_rotate(t, p);
r_node_rotate(t, g);
}
else if(n-> p_node-> l_node == n && p-> p_node-> r_node == p) {
r_node_rotate(t, p);
l_node_rotate(t, g);
}
}
}
}
void insert(sPlayTree_DS *t, node *n) {
node *y = NULL;
node *temp = t-> root_node;
while(temp != NULL) {
y = temp;
if(n->data < temp->data)
temp = temp-> l_node;
else
temp = temp-> r_node;
}
n-> p_node = y;
if(y == NULL) //newly added node is root_node
t-> root_node = n;
else if(n->data < y->data)
y-> l_node = n;
else
y-> r_node = n;
splay(t, n);
}
node* search(sPlayTree_DS *t, node *n, int x) {
if(x == n->data) {
splay(t, n);
return n;
}
else if(x < n->data)
return search(t, n-> l_node, x);
else if(x > n->data)
return search(t, n-> r_node, x);
else
return NULL;
}
void delete(sPlayTree_DS *t, node *n) {
splay(t, n);
sPlayTree_DS * l_node_subtree = new_sPlayTree_DS();
l_node_subtree-> root_node = t-> root_node-> l_node;
if( l_node_subtree-> root_node != NULL)
l_node_subtree-> root_node-> p_node = NULL;
sPlayTree_DS * r_node_subtree = new_sPlayTree_DS();
r_node_subtree-> root_node = t-> root_node-> r_node;
if( r_node_subtree-> root_node != NULL)
r_node_subtree-> root_node-> p_node = NULL;
free(n);
if( l_node_subtree-> root_node != NULL) {
node *m = maximum( l_node_subtree, l_node_subtree-> root_node);
splay( l_node_subtree, m);
l_node_subtree-> root_node-> r_node = r_node_subtree-> root_node;
t-> root_node = l_node_subtree-> root_node;
}
else {
t-> root_node = r_node_subtree-> root_node;
}
}
void inorder(sPlayTree_DS *t, node *n) {
if(n != NULL) {
inorder(t, n-> l_node);
printf("%d\n", n->data);
inorder(t, n-> r_node);
}
}
int main() {
sPlayTree_DS *t = new_sPlayTree_DS();
node *p, *q, *r, *s, *t, *u, *v, *w, *x, *y, *z, *a, *b;
p = n_node(10);
q = n_node(20);
r = n_node(30);
s = n_node(100);
t = n_node(90);
u = n_node(40);
v = n_node(50);
w = n_node(60);
x = n_node(70);
y = n_node(80);
z = n_node(150);
a = n_node(110);
b = n_node(120);
insert(t, p);
insert(t, q);
insert(t, r);
insert(t, s);
insert(t, t);
insert(t, u);
insert(t, v);
insert(t, w);
insert(t, x);
insert(t, y);
insert(t, z);
insert(t, a);
insert(t, b);
delete(t, p);
delete(t, b);
inorder(t, t-> root_node);
return 0;
}
Output:
Conclusion
Splay tree is a data structure similar to the binary tree but has the capability of self-balancing. The splay is the operation carried out after performing any other operation on the tree which involves rearrangement of the nodes in such a way that the node on which the operation is being done is brought to root.
Recommended Articles
This is a guide to Splay Tree in Data Structure. Here we also discuss the introduction and operations in splay tree along with examples. You may also have a look at the following articles to learn more –