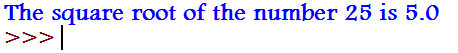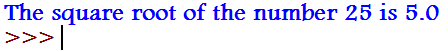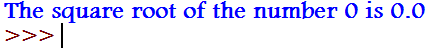Updated April 14, 2023
Introduction to Square Root in Python
Conversely, the square root of a number is a value that gives the original number when multiplied by itself. Every positive number has got two square roots. (same value with positive and negative signs.) The following is the notation of Square Root: –
√25 = ±5
For a negative number, the square root of the number includes the complex numbers, the discussion of which is out of scope for this article.
Mathematical Intuition of Square
We all have learned in our childhood that when a number is multiplied by itself, we get the square of that number. Square of a number can be alternately thought of as multiplying a number that many numbers of times. Let us try to understand it with the help of an example: –
Let us suppose we want to get the square of 5. If we multiply the number (in this case, 5) by 5 times, we get the square of that number. The following notation denotes the square of the number: –
52 = 25
Square Root in Python
In Python, we also need to use the square root functionality very frequently in our programming. There are multiple ways in which we can find the square root of a number in Python.
1. Using Arithmetic Operator (power)
Code:
num = 25
sqrt = num ** (0.5)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
Explanation: We can make use of the “**” operator in Python to get the square root of a number. Any number raised to the power of half, i.e. 0.5, gives us the number’s square root.
2. Using math.sqrt()
The square root of a number can be obtained using the sqrt function from python’s math module, as shown above. Henceforth, we would see three scenarios in which we would give positive, zero and negative numbers in an argument of the function and see the result.
a. Giving a positive number as an argument.
Code:
import math
num = 25
sqrt = math.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
b. Giving zero as an argument.
Code:
import math
num = 0
sqrt = math.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
c. Giving a negative number as an argument.
Code:
import math
num = -25
sqrt = math.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
Explanation: When we give a negative number as an argument, we get the following math domain error. So the argument must be greater than 0. So to tackle this issue, we must use the sqrt function from the cmath module.
3. Using cmath.sqrt()
following are the examples using cmath.sqrt():
a. Giving a negative number as an argument.
Code:
import cmath
num = -25
sqrt = cmath.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
Explanation: For negative numbers, we must use the sqrt function of the cmath module, which deals with mathematical computation on complex numbers.
b. Giving a complex number as an argument.
Code:
import cmath
num = 4 + 9j
sqrt = cmath.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
Explanation: For finding the square root of complex numbers also we can use the cmath.sqrt() function.
4. Using np.sqrt()
Code:
import numpy as np
num = -25
sqrt = np.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
Explanation: The square root of a positive, zero, and complex number can be calculated with the help of the above function.
5. Using scipy.sqrt()
Code:
import scipy as sc
num = 25
sqrt = sc.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
Explanation: Like numpy sqrt function in scipy, also the square root of positive, zero and complex numbers can be calculated successfully, but for negative numbers, nan is returned with RunTimeWarning.
6. Using sympy.sqrt()
Code:
import sympy as smp
num = 25
sqrt = smp.sqrt(num)
print("The square root of the number "+str(num)+" is "+str(sqrt))Output:
Explanation: The sympy is a module for the python module for symbolic mathematics. With the help of sympy.sqrt() function we can get the square root of positive, zero, negative and complex numbers. The only difference between this method and other methods are in this method when the argument is an integer, then the square root is also an integer, unlike the other cases where the square root is always floating no matter the datatype of the argument.
Conclusion
Finally, we come to the closure of this article in which we had a brief introduction to square root function in mathematics. Then we discussed the internal functionality of a square root function and its implementation. We finally concluded by looking at the different methods of applying the square root function in Python.
Recommended Articles
We hope that this EDUCBA information on “Square Root in Python” was beneficial to you. You can view EDUCBA’s recommended articles for more information.