Updated July 6, 2023
Introduction to Squeeze Matlab
The ‘Squeeze’ command in Matlab operates like the ‘reshape’ command. As we know, reshape is used to change or modify the size or dimensions of arrays or vectors, or multidimensional matrix. Similarly, the squeeze is also used to reshape arrays, vectors, and multidimensional matrix dimensions. The only difference between reshaping and squeeze is that reshape operates according to the user’s given parameters and dimensions. Still, the squeeze is used to remove singleton dimensions of the matrix. Thus, it directly eliminates the singleton dimensions and adjusts the elements accordingly.
Syntax:
1. Output = squeeze ( input )
output variable name = squeeze (input variable name)
2. size ( input)
size (output)
size ( variable name ) # to observe changes in dimensions.
How does Squeeze Matlab Work?
The squeeze function works on the dimensions of the multidimensional matrix. It ignores or eliminates the singleton dimension of the input matrix. It squeezes changes in shape or dimensions of input but does not change the values of elements, meaning it stores the data as it is. To use this function, first, we need to assign one multi-dimensional matrix with singleton dimensions .then we can apply the squeeze function to input using the above syntax. After getting the output, we cannot observe the changes because the elements will look as it is. Therefore to check the changes in output, we need to check the size of the input and the size of the output. It will be different in input and output.
Examples of Squeeze Matlab
Different examples are mentioned below:
Example #1
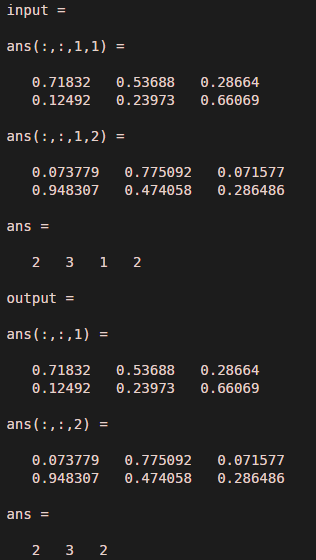
In this example, we have considered one input in the form of a multi-dimensional matrix as variable ‘input.’ the dimensions of the matrix are two by three by one by two. In this example, dimensions represent two rows and three columns with two different random matrices. Here ‘rand’ represents random elements of the matrix. If we observe the output of example 1, then elements of input and output are the same, but the shape or we can size of matrices is different. The size of the input is ( 2, 3, 1, 2 ), and the size of the output is ( 2, 3, 2 ). That means squeeze eliminates dimension one from the input.
Code:
clc ;
clear all ;
input = rand(2, 3,1,2)
size ( input )
output = squeeze (input)
size (output )Output:
Example #2
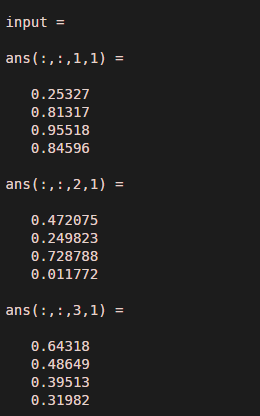
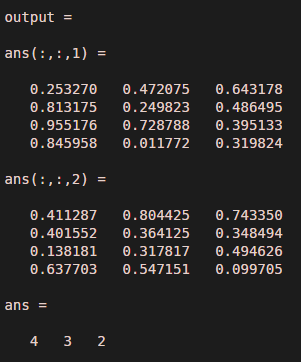
In Example 2, we assume one more random multidimensional matrix with dimensions four by one by three by two. Thus, there are four rows and one column with three multidimensional matrices. If we observe the output, it eliminates the singleton dimension, and the size of the new matrix will be (4, 3, 2 ), meaning there will be four rows and three columns with two different matrices.
Code:
clc ;
clear all ;
input = rand (4, 1, 3, 2 )
size ( input )
output = squeeze ( input )
size ( output )Output:
Example #3
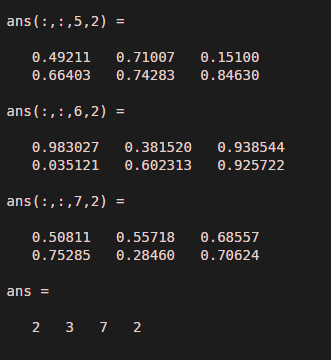
In this example, we considered more dimensions in the input matrix with two singleton dimensions. Thus, the dimensions of the input matrix are two by three by one by seven by one by two ( 2, 3, 1, 7, 1, 2 ). If we observe the output, both the singleton dimensions are removed, and a new matrix size becomes ( 2, 3, 7, 2). there will be two rows and three columns with seven different matrices.
Code:
clc ;
clear all ;
input = rand ( 2, 3, 1 , 7, 1, 2 )
size ( input )
output = squeeze ( input )
size ( output)Output:
Conclusion
The squeeze function is important because it changes the dimension but does not ignore the data or elements of the matrix. That means there is no loss of information. As we observe in the above example, some dimensions are logically useless while implemented. Still, unnecessary if it occupies storage, so with the help of this function, we can directly ignore the singleton dimension.
Recommended Articles
We hope that this EDUCBA information on “Squeeze Matlab” was beneficial to you. You can view EDUCBA’s recommended articles for more information.