Overview of Strong Number in Python
Strong Number in Python in this article. If, for a number, the sum of the factorial of each of the digits of the number equals the given number, then such a number is called a strong number. Example is 145 as 1! + 4! + 5! = 1 + 24 + 120 = 145.
The logic behind a strong number
In order to check if a number is a strong number or not, the first step is to divide each of the digits of the number as individual units. Next, we have to take the factorial of each of the digits. Then we will sum the values obtained for each of the digits after they are subjected to the factorial operation. Finally, it has to be checked if this sum equals to the given number. If yes, then the number is a strong number.
We can have the below algorithm as a generic method to check if a given number is a strong number or not.
- Get the desired number as input for verifying if it is a strong number or not. Let’s have a variable N to store this input number.
- Copy the value of N into a temporary variable, say temp_N.
- Initialize a variable, say ‘sum’ to zero. This will store the sum of the factorial of each of the digits of N.
- The last digit of the number must be stored in some variable, say last_digit = N % 10
- The factorial of last_digit must be stored in a variable, say fact.
- Each time the factorial of the last digit is found, it should be added to the sum. sum = sum + fact
- After every factorial operation, the number must be reduced in terms of units by dividing 10. N = N / 10
- Repeat the steps 4 to 7, till N > 0.
- After the loop is over, it should be checked if the sum equals the number, i.e. sum = temp_N. If yes, then the input number is a strong number.
Using Python to implement a Strong number program
The following Python program code implemented using the algorithm described above helps us to determine if a number is a strong number or not.
Example #1
Code:
sum = 0
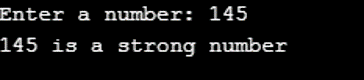
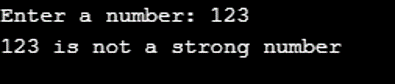
N = int(input("Enter a number: "))
temp_N = N
while(N):
k = 1
fact = 1
r = N % 10
while(k <= r):
fact = fact * k
k = k + 1
sum = sum + fact
N = N//10
if(sum == temp_N):
print(str(temp_N) + " is a strong number")
else:
print(str(temp_N) + " is not a strong number")Output:
Initially, when the program is executed, the user is asked to pass the input. We can pass the required number for checking it’s a strong number or not. In this case, we passed 145 and pressed enter. The output returned is “145 is a strong number”, which is correct. The below screenshot illustrates this.
Let’s pass another input. This time we passed 123. As 123 is not a strong number so, we got the output as shown below.
The above program code that we saw performs to check for just a single number. At times, we may need to simultaneously verify this for multiple numbers. For this, we will use another approach in Python. The following Python program code helps us to accomplish this. Carefully go through the following Python programming code, and see how each of its elements performs its very role in the code.
Example #2
Code:
# Compute factorial
def fact_N(N):
if(N == 0 or N == 1):
fact = 1
else:
fact = N * fact_N(N - 1)
return fact
# Check for strong number
def strong_number(list):
n_list =[]
for i in list:
temp_N = i
sum = 0
while(temp_N):
r = temp_N % 10
sum += fact_N(r)
temp_N = temp_N // 10
if(sum == i):
n_list.append(i)
else:
pass
return n_list
# Input
input_vals = [1, 2, 5, 121, 145, 788, 47, 193, 2100]
strong_num_list = strong_number(input_vals)
print(strong_num_list)The above Python program code is composed of three parts. First, the fact_N() function that calculates the factorial of the number passed into it as a parameter. Second, we have the strong_number() function that calculates the sum of the factorial of each of the digits of the given number. As we intend to list multiple values as an input, the strong_number() function takes a list as a parameter. A blank list n_list is created in the strong_number routine. Using a while loop, the sum of the factorials of each digit is calculated. Finally, it is checked if the sum equals the given number; if yes, it is returned by the routine. The third part of the program is the input section. We can pass the required values by just specifying them and executing the program. The list is passed into the strong_number function, and the strong number(s) returned are stored in the strong_num_list variable, which is a list variable. Finally, we print the list of all possible string values from the list.
Output:
As we can see above, we got a list containing 1, 2, and 145 from the input list of values as output. The result is correct. Let’s check the program by passing another set of values.
Example #3
Code:
# Compute factorial
def fact_N(N):
if(N == 0 or N == 1):
fact = 1
else:
fact = N * fact_N(N - 1)
return fact
# Check for strong number
def strong_number(list):
n_list =[]
for i in list:
temp_N = i
sum = 0
while(temp_N):
r = temp_N % 10
sum += fact_N(r)
temp_N = temp_N // 10
if(sum == i):
n_list.append(i)
else:
pass
return n_list
# Input
input_vals = [3, 6, 17, 49, 231, 455, 1010, 663, 124, 980]
strong_num_list = strong_number(input_vals)
print(strong_num_list)Output:
As can be seen above, a blank list has been returned as output. So, none of the values in the list is a strong number.
Conclusion
A strong number is a mathematical concept that has its own applications. Python allows us to implement strong number checking programs quickly and effectively through its multiple features.
Recommended Articles
This is a guide to Strong Number in Python. Here we discuss the introduction, the logic behind a strong number, and Python to implement a Strong number program. You can also go through our other related articles to learn more–