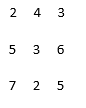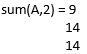Updated March 22, 2023

Introduction to Sum Function in Matlab
MATLAB is a language used for technical computing. As most of us will agree, an easy to use environment is a must for integrating tasks of computing, visualizing and finally programming. MATLAB does the same by providing an environment that is not only easy to use but also, the solutions that we get are displayed in terms of mathematical notations which most of us are familiar with. In this article, we will look in-depth at the Sum Function in Matlab.
Uses of Matlab Include (But Not Limited To)
- Computation
- Development of Algorithms
- Modeling
- Simulation
- Prototyping
- Data analytics (Analysis and Visualization of data)
- Engineering & Scientific graphics
- Application development
MATLAB provides its user with a basket of functions, in this article we will understand a powerful function called ‘Sum function’.
Syntax:
S = sum(A)
S = sum(A, dim)
S = sum(A, vecdim)
S = sum(__, outtype)
S = sum(__, nanflag)
Description of Sum Function in Matlab
Now let us understand all these functions one by one.
1. S = sum(A)
- This will return the sum of all the elements of ‘A’ along the dimension of the array which is non-singleton i.e. the size is not equal to 1 (It will consider the first dimension which is non-singleton).
- sum(A) will return the sum of the elements if A is vector.
- sum(A) will return a row vector which will have some of each column if A is a matrix.
- If A is a multidimensional array, sum(A) will operate along the 1st array dimension whose size is not equal to 1 and will treat all the elements as vectors. This dimension will become 1 and the size of other dimensions will not be changed.
Now Let us understand sum(A) with an example. But before that, please keep in mind that in MATLAB, matrices have the following dimensions:
1=rows, 2=columns, 3=depth
Example #1 – When we have both rows & columns
As explained above, sum(A) will do the addition along the 1st dimension which is non-singleton. For a single row/column, we will get the result as one number.
A = [1, 3, 7 ; 5, -8, 1];
S = sum(A);
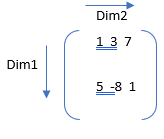
Here 1 is the first non-singleton dimension (the dimension whose length is not equal to 1). So, some will be along with the row elements i.e. going down.
S = sum(A) = 6 -5 8
Example #2 – When we have only 1 row
A = [2, 3, 7 ];
B = sum(A);
Here first non-singleton dimension is 2 (i.e. columns). So, the sum will be along with the column elements
B = sum(A) = 12
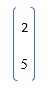
Example #3 – When we only have 1 column
A = [2 ; 5];
So, A =
Here, the first non-singleton dimension is 1, so the sum will be along with the row elements.
B = sum(A) = 7
2. S = sum(A, dim)
This function will return sum along the dimension passed in argument.
Example
A = [2 4 3; 5 3 6; 7 2 5]
So, A =
S = sum(A,2)
Here we have passed ‘2’ as an argument, so the sum will be along dimension 2.
So, S =
3. S = sum(A, vecdim)
This function will sum the elements based on the dimensions that are specified in the vector ‘vecdim’. For eg. if we have a matrix, then the sum(A,[1 2]) will be the sum of all the elements in A, because every element of matrix A will be contained in the slice of the array defined by dimensions 1 & 2 (Remember that dimension 1 is for Rows and 2 is for columns)
Example
A = ones(3,3,2); (This will create a 3-D array whose all elements are equal to 1)
Now, To sum all the elements present in each slice of matrix A, we need to specify the dimensions which we want to sum (both row & column). We can do this by providing a vector dimension as an argument. In our example, both the slices are a 3 * 3 matrix of ones, so the sum will be 9.
S1 = sum(A,[1 2])
So, S1 = S1(:, :, 1) = 9
&
S1(:, :, 2) = 9
4. S = sum(A, outtype)
This function will return the sum with the data type passed in the argument. The ‘outtype’ can be ‘native’, ‘default’ or ‘double’.
Example
A = int32(5: 10);
S = sum(A, 'native')
Output for this will be,
S = int32
45
Where int32 is the native data type of elements of A and 45 is the sum of the elements from 5 to 10.
5. S = sum(nanflag)
This will specify if we need to include or omit NaN from our calculations.
sum(A, ‘includenan’) will include all the NaN values that are present in the calculation.
sum(A, ‘omitnan’) will ignore all the NaN values.
Example
A = [1 -5 3 -2 NaN 4 NaN 9];
S = sum(A, 'omitnan')
So, the output that we will get is
S = 10
(After ignoring all the NaN values)
Conclusion
So, as we can see, MATLAB is a system whose basic data element is an array that does not require any dimensioning. This allows us to solve computing problems, especially the problems with matrix & vector formulations. All this is done in a significantly less amount of time when compared to writing a program in a scalar and non-interactive language such as C.
Recommended Articles
This is a guide to Sum Function in Matlab. Here we discuss the uses of Matlab, syntax, examples along with the description of sum function in Matlab respectively. You may also look at the following articles to learn more –